[ARC053D]2 つの山札

题意：给定排列$a_{1\cdots n},b_{1\cdots n}$，执行以下操作$2n-2$次来生成一个长度为$2n-2$的序列：选择$a,b$之一（选择的序列长度要$\geq2$），删除它的第一个数字并将另一个序列的第一个数字加到生成的序列的末尾，问最后能生成多少种不同的序列

首先是一个转化，画一个$n\times n$的网格，第$i$行的$n-1$条边上的数字为$a_i$，第$i$列的$n-1$条边上的数字为$b_i$，一个生成的序列对应着这个网格上从左上角到右下角的一条路径上的数字

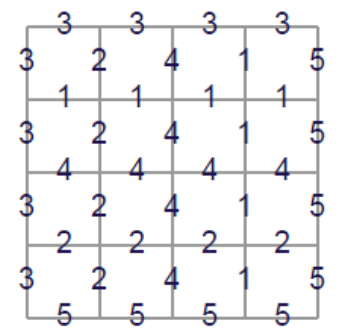
对于$a=\{3,1,4,2,5\},b=\{3,2,4,1,5\}$，题解给了以上这张对应的图

考虑DP，设$f_{i,j}$表示走到$(i,j)$的不同方案数，直接转移就是$f_{i,j}=f_{i-1,j}+f_{i,j-1}$，但如果$a_i=b_j$，那么这样可能产生重复

考虑所有使得$a_{i-k}=b_{j-k}(k\geq1)$的$k$，如果从某个$(i-k,j-k)$走到$(i,j)$只经过这些$(i-k',*)$和$(*,j-k')$，那么一条从$(i-k,j-k)$到$(i,j)$且不碰对角线的路径，沿对角线对称可以得到路径不同但得到数列相同的方案，我们要减去这些方案，即$\sum\limits_{k\geq1}[a_{i-k}=b_{i-k}]f_{i-k,j-k}C_{t-1}$，其中$C_n$是卡特兰数，$t$为当前是第几个满足要求的$k$

答案即为$f_{n,n}$，因为只会有$n$对$a_i=b_j$，所总时间复杂度为$O(n^2)$

#include<stdio.h>
typedef long long ll;
const int mod=1000000007;
int mul(int a,int b){return(ll)a*b%mod;}
int pow(int a,int b){
	int s=1;
	while(b){
		if(b&1)s=mul(s,a);
		a=mul(a,a);
		b>>=1;
	}
	return s;
}
int fac[2010],rfac[2010];
void pre(int n){
	int i;
	fac[0]=1;
	for(i=1;i<=n;i++)fac[i]=mul(fac[i-1],i);
	rfac[n]=pow(fac[n],mod-2);
	for(i=n;i>0;i--)rfac[i-1]=mul(rfac[i],i);
}
int C(int n){return mul(fac[2*n],mul(rfac[n],rfac[n+1]));}
int a[1010],b[1010],f[1010][1010];
int main(){
	int n,i,j,k,s;
	scanf("%d",&n);
	pre(n*2);
	for(i=1;i<=n;i++)scanf("%d",a+i);
	for(i=1;i<=n;i++)scanf("%d",b+i);
	f[1][1]=1;
	for(i=1;i<=n;i++){
		for(j=1;j<=n;j++){
			if(i>1||j>1)f[i][j]=(f[i-1][j]+f[i][j-1])%mod;
			if(a[i]==b[j]){
				s=0;
				for(k=1;i-k>0&&j-k>0;k++){
					if(a[i-k]==b[j-k])(f[i][j]-=mul(C(s++),f[i-k][j-k]))%=mod;
				}
			}
		}
	}
	printf("%d",(f[n][n]+mod)%mod);
}