LeetCode 笔记系列 18 Maximal Rectangle [学以致用]

题目： Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing all ones and return its area.

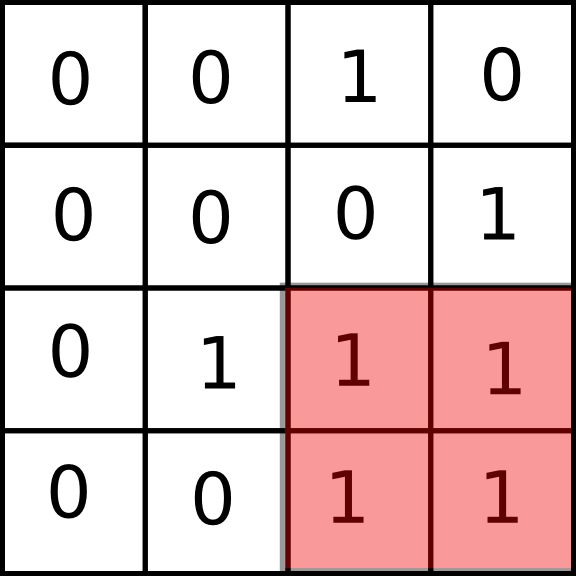
leetcode的题目真是越来越经典了。比如这个题目，就是一道男默女泪的题。

一般人拿到这个题目，除非做过类似的，很难一眼找出一个方法来，更别说找一个比较优化的方法了。

首先一个难点就是，你怎么判断某个区域就是一个矩形呢？

其次，以何种方式来遍历这个2D的matrix呢？

一般来说，对这种“棋盘式”的题目，像什么Queen啦，象棋啦，数独啦，如果没有比较明显的遍历方式，可以采用一行一行地遍历。（好像废话哦。。。）

然后，当遍历到(i, j)的时候，该做什么样的事情呢？想想，嗯，那我可不可以简单看看，以(i,j)为矩形左上角，能不能形成一个矩形，能不能形成多个矩形？那形成的矩形中，我们能不能找一个最大的呢？（有同学问，为毛你要以这个点为左上角，不为左下角，或者其他脚哩？因为我们打算从左到右，从上到下一行一行遍历嘛，这样就不会漏掉，说不定还能做一些优化）

首先，如果(i, j)是0，那肯定没法是矩形了。

如果是1，那么我们怎么找以它为左上角的矩形呢？呼唤画面感！

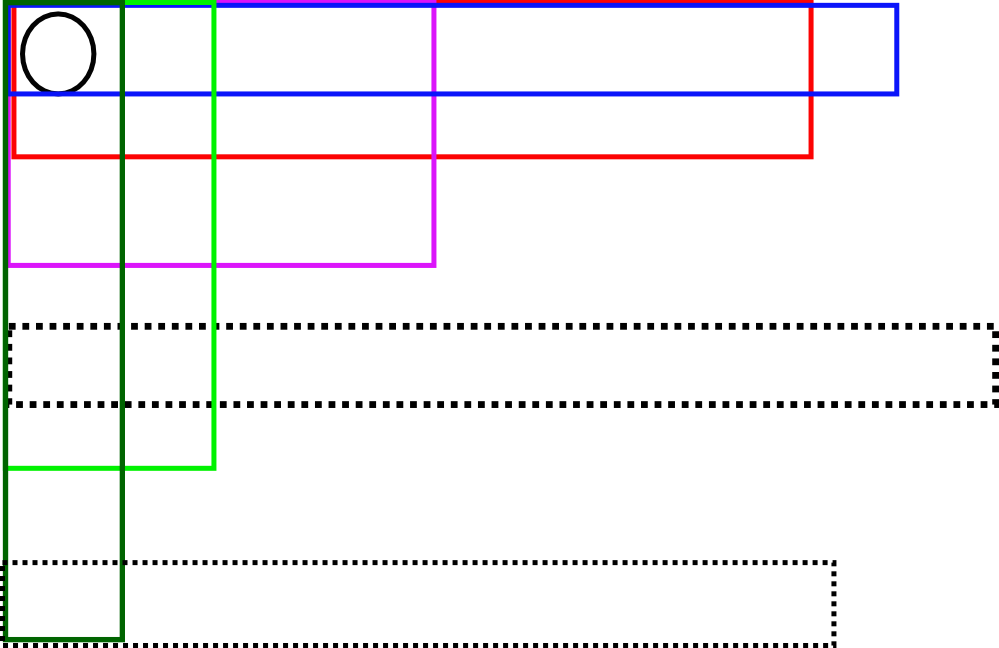
。。。你TM在逗我？==b

图中圈圈表示左上角的1，那么矩形的可能性是。。。太多啦，怎么数嘛！

我们可以试探地从左上角的1所在的列开始，往下数数，然后呢，比如在第一行，例如是蓝色的那个矩形，我们看看在列上，它延伸了多远，这个面积是可以算出来的。

然后继续，第二行，例如是那个红色的矩形，再看它延伸到多远，哦，我们知道，比第一行近一些，我们也可以用当前离第一行的行数，乘以延伸的距离，得到当前行表示的矩形面积。

但是到了第一个虚线的地方，它远远超过了上面的其他所有行延伸的距离了，注意它的上方都是空心的哦，所以，我们遇到这种情况，计算当前行和左上角1围成的面积的时候，只能取所有前面最小的延伸距离乘以当前离第一行的行数。其实，这对所有情况都是这样的，是吧？于是，我们不是就有方法遍历这些所有的矩形了嘛。

代码如下：

     /**
      * 以给出的坐标作为左上角，计算其中的最大矩形面积
      * @param matrix
      * @param row 给出坐标的行
      * @param col 给出坐标的列
      * @return 返回最大矩形的面积
      */
     private int maxRectangle(char[][] matrix, int row, int col) {
         int minWidth = Integer.MAX_VALUE;
         int maxArea = 0;
         for (int i = row; i < matrix.length && matrix[i][col] == '1'; i++) {
             int width = 0;
             while (col + width < matrix[row].length
                     && matrix[i][col + width] == '1') {
                 width++;
             }
             if (width < minWidth) {// 如果当前宽度小于了以前的最小宽度，更新它，为下面的矩形计算做准备
                 minWidth = width;
             }
             int area = minWidth * (i - row + 1);
             if (area > maxArea)
                 maxArea = area;
         }
         return maxArea;
     }

maxRectangle

这样，我们再对每个点都调用一下上面的这个方法，不是就能求出最大面积了么。

解法一：

public int maximalRectangle(char[][] matrix) {
        // Start typing your Java solution below
        // DO NOT write main() function
        int m = matrix.length;
        int n = m == 0 ? 0 : matrix[0].length;
        int maxArea = 0;
        for(int i = 0; i < m; i++){//row
            for(int j = 0; j < n; j++){//col
                if(matrix[i][j] == '1'){
                    int area = maxRectangle(matrix, i, j);
                    if(area > maxArea) maxArea = area;
                }
            }
        }
        return maxArea;
     }

这个需要O(n³)，所以没有通过大集合的测试。

leetcode的讨论组给出了一个比较难理解的方法，这里就不采用了。

说说第三个方法。前一个笔记，我们讨论了柱状图的最大矩形面积，那可以O(n)的，学以致用呀！btw，leetcode的这两题也是挨一块儿的，用心良苦。。。。

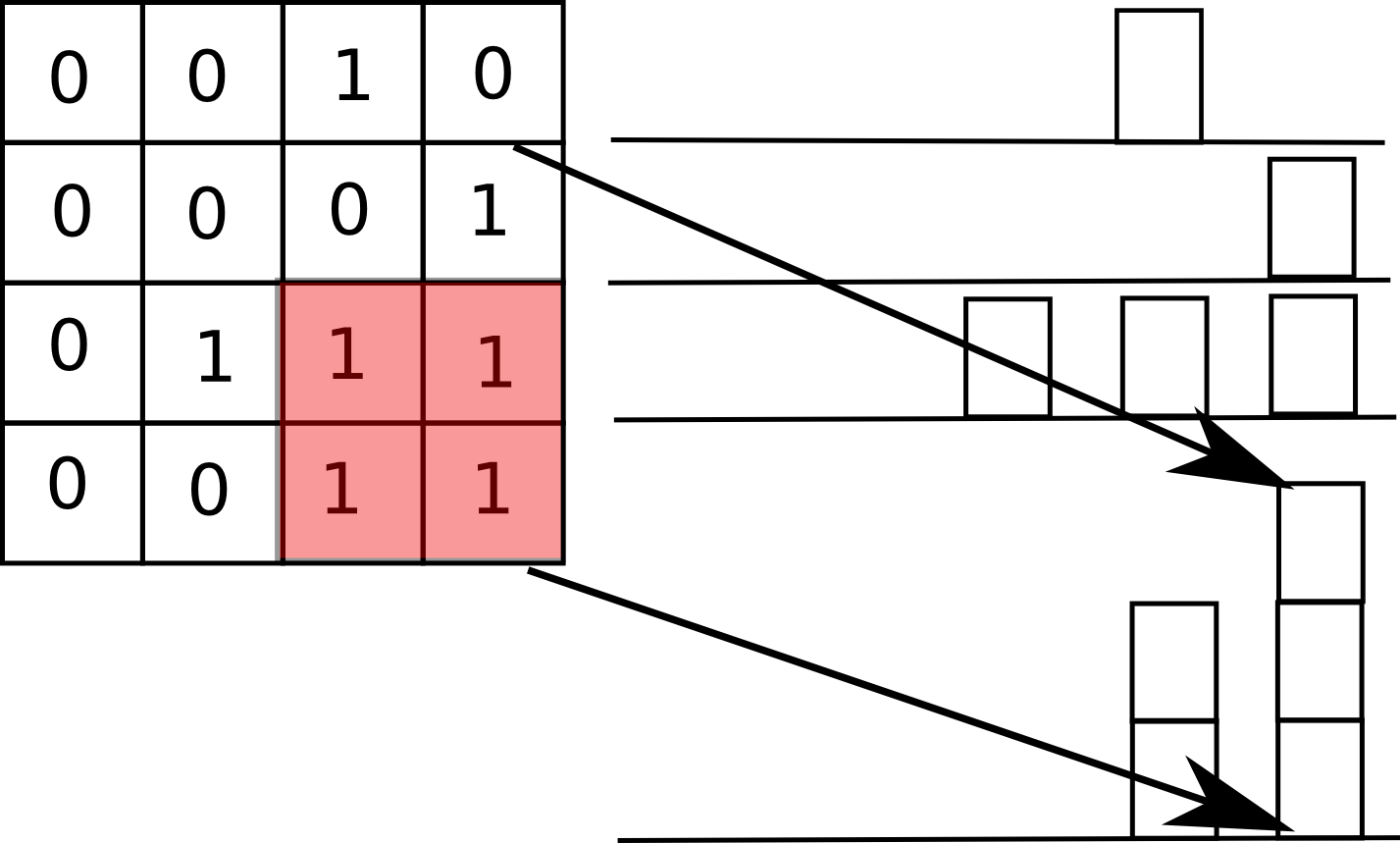
如果我们把每一行看成x坐标，那高度就是从那一行开始往上数的1的个数。带入我们的maxAreaInHist方法，在O(n²)时间内就可以求出每一行形成的“柱状图”的最大矩形面积了。它们之中最大的，就是我们要的答案。

代码如下：

 public int maximalRectangle2(char[][] matrix) {
         int m = matrix.length;
         int n = m == 0 ? 0 : matrix[0].length;
         int[][] height = new int[m][n + 1];
         //actually we know that height can just be a int[n+1],
         //however, in that case, we have to write the 2 parts together in row traverse,
         //which, leetcode just doesn't make you pass big set
         //所以啊，leetcode是喜欢分开写循环的，即使时间复杂度一样，即使可以节约空间
         int maxArea = 0;
         for(int i = 0; i < m; i++){
             for(int j = 0; j < n; j++) {
                 if(matrix[i][j] == '0'){
                     height[i][j] = 0;
                 }else {
                     height[i][j] = i == 0 ? 1 : height[i - 1][j] + 1;
                 }
             }
         }
         for(int i = 0; i < m; i++){
             int area = maxAreaInHist(height[i]);
             if(area > maxArea){
                 maxArea = area;
             }
         }
         return maxArea;
      }

      private int maxAreaInHist(int[] height){
          Stack<Integer> stack = new Stack<Integer>();
          int i = 0;
          int maxArea = 0;
          while(i < height.length){
              if(stack.isEmpty() || height[stack.peek()] <= height[i]){
                  stack.push(i++);
              }else {
                  int t = stack.pop();
                  maxArea = Math.max(maxArea, height[t] * (stack.isEmpty() ? i : i - stack.peek() - 1));
              }
          }
          return maxArea;
      }

这里有一个和leetcode相关的细节。就是本来在计算height数组的时候，我们没有必要分配成代码中的那个样子，一维就可以了，然后在遍历每一行的时候计算当前行的height数组，然后再计算maxArea。这种情况下还是过不了大集合，所以不得不为每一行都保存一个height，先期计算该二维数组。

总结：

1. 学到的新知识要用；

2. 画面感和逻辑分析都很重要，不可偏非。