牛客网提高组模拟赛第五场 T1同余方程（异或）（位运算）

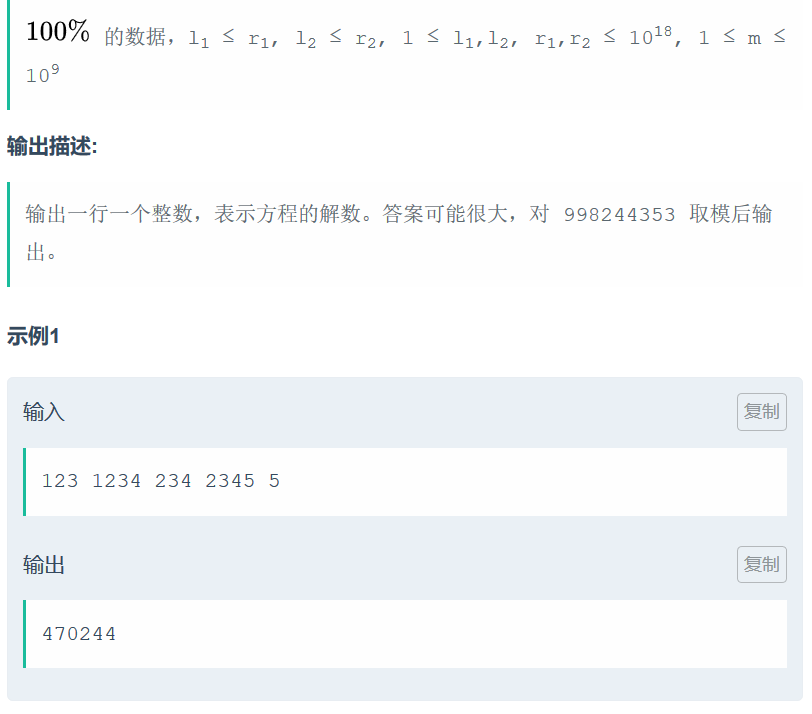
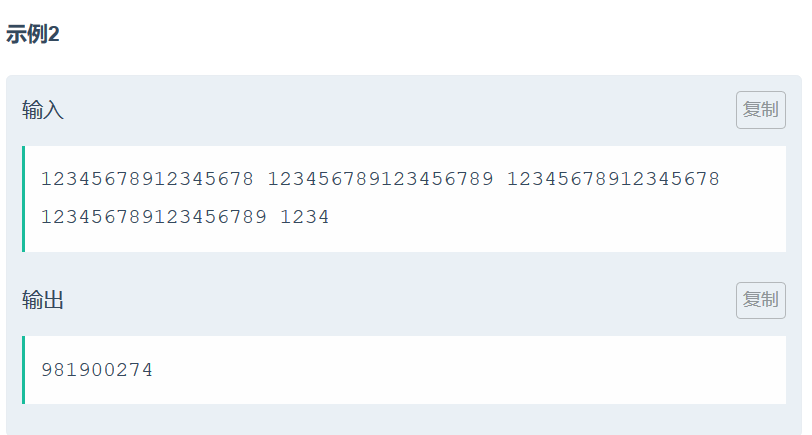
区间不好做，但是我们可以转化成前缀来做。转化为前缀之后之后就是二维前缀和。

但是我还是不怎么会做。所以只能去看吉老师的题解 （确定写的那么简单真的是题解？？？）。

我们要求模一个数余0，就等于找它的倍数。找它的倍数自然只要知道区间就可以了。

题解上面说：如果\(r1=2^n\)，\(r2=2^m\)，不妨设 \(n<=m\)，那么结果一定在区间 \([0,2^n)\)中，而 且每一个值出现了 \(2^m\) 次

这是很显然的，因为按照异或的运算法则来讲，不可能会有比r1最高位1还高的位出现。而且考虑在二进制下，还有多种不同的方式可以凑成这个数。

之后我们考虑更一般的情况。

我们把高位确定下来，之后摆放低位。两两之间统计答案。

怎么理解呢，就是先把最高位的1确定下来，然后后面显然1就可以随便放了（反正使得当前位1变成0，后面（比它小的）的所有数都可以达到了）。我们考虑遍历枚举的两个边界的最高位1的位数，然后计算这种组合能够达到的范围（啊啊啊语文能力又下线了。。。怎么办。。大家看一下代码？？？），知道范围之后就容易能够知道有多少个所求数的倍数了。之后按照上面解释的，我们可以统计出有多少种不同的x,y组合方式达到这个异或值。

因为感觉自己说的很不清楚，所以代码里加了一点注释qwq。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define mod 998244353
#define ll long long
using namespace std;
ll kkk,ans,a,b,c,d;
ll calc(ll a,ll b){
    ll ansans=0;
    for(int i=0;i<=63;++i)
	{
        //因为在long long范围内，所以遍历到63
		if(((a>>i)&1)==0) continue;
        //如果该位不是1就跳过
        for(int j=0;j<=63;++j)
		{
            if(((b>>j)&1)==0) continue;
            //同上
            ll l=((a-(1ll<<i))^(b-(1ll<<j)))&(~((1ll<<max(i,j))-1));
            //因为我们已经确定max(i,j)为最高位1了
			//所以前面的值就不变了，直接异或就行
			//后面的max(i,j)位经过处理全变成0（与操作和后面的东西就是这个用）
			//&(~((1<<n)-1))表示将后面的n位全部变成0
            ll r=l+(1ll<<max(i,j))-1;
            //因为是左闭右开区间
            ll cnt=(r/kkk)-l/kkk+(l%kkk==0);
            //注意左闭，所以如果正好是倍数的话还是要加上1
            tmp%=mod;
            ansans=(ansans+(cnt*((1LL<<min(i,j))%mod))%mod)%mod;
            //注意及时取模qwq
			//其实像我这样写不好，最好分步写，避免中间没有取模爆long long
			//哦，还要注意左移右移的运算级很低，所以即使加括号
        }
    }
    return ansans;
}
int main()
{
    freopen("ce.in","r",stdin);
	scanf("%lld %lld %lld %lld %lld",&a,&b,&c,&d,&kkk);
    ll ans=calc(b+1,d+1);
    ans=(ans+mod-calc(c,b+1))%mod;
    ans=(ans+mod-calc(a,d+1))%mod;
    ans=(ans+calc(a,c))%mod;
    //类比二维前缀和
    printf("%lld\n",ans%mod);
    return 0;
}