LDA线性判别分析

给定训练集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能的近，异类样例点尽可能的远，对新样本进行分类的时候，将新样本同样的投影，再根据投影得到的位置进行判断，这个新样本的类别

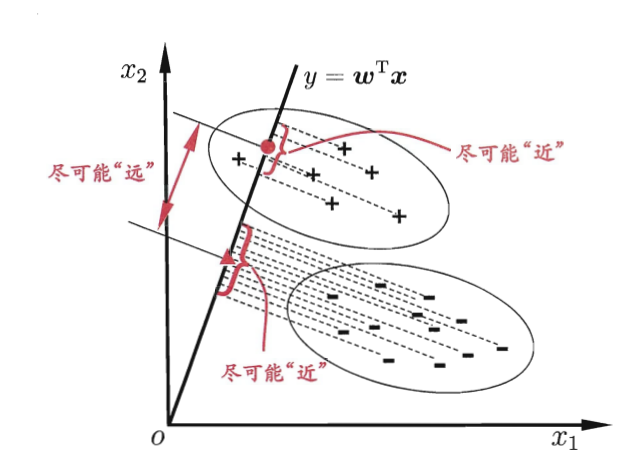
LDA二维示意图。用‘+’表示正类“-”表示负类，两个投影，实心三角形和圆表示投影中心

二分类：

给定数据集

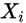:第类的样本集合

:第类的均值向量

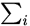:第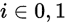类的协方差矩阵

将数据投影在直线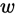上,则两类样本的中心点在直线上的投影分别为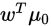和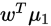

将所有的样本点投影到直线上之后，两类样本的协方差为 和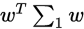

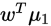
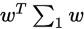由于直线是一维空间，因此 和均为实数

为了把两类分的比较开于是有两个方面考虑

1、同类抱团更加紧密

2、不同类分的开

为了让同类的样本尽可能的接近，就让同类样本的投影点协方差尽可能的小，

于是有

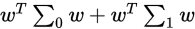让他们尽可能的小

为了两类分的开：

于是有了两类的投影中心尽可能的远离

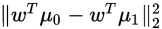
要尽可能的大，这样就可以得到它的优化目标函数，使她最大就ok

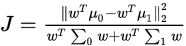
定义两个符号

类内散度矩阵：



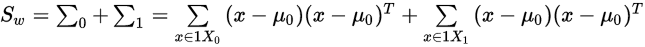
类间散度矩阵

于是得到了要优化的下式,最后需要优化的目标，使之最大化即可，求取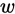

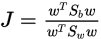
LDA线性判别分析的更多相关文章

  1. PCA主成分分析 ICA独立成分分析 LDA线性判别分析 SVD性质

    机器学习(8) -- 降维 核心思想:将数据沿方差最大方向投影,数据更易于区分 简而言之:PCA算法其表现形式是降维,同时也是一种特征融合算法. 对于正交属性空间(对2维空间即为直角坐标系)中的样本点 ...

  2. LDA线性判别分析原理及python应用（葡萄酒案例分析）

    目录 线性判别分析(LDA)数据降维及案例实战 一.LDA是什么 二.计算散布矩阵 三.线性判别式及特征选择 四.样本数据降维投影 五.完整代码 结语 一.LDA是什么 LDA概念及与PCA区别 LD ...

  3. LDA 线性判别分析

    LDA, Linear Discriminant Analysis,线性判别分析.注意与LDA(Latent Dirichlet Allocation,主题生成模型)的区别. 1.引入 上文介绍的PC ...

  4. LDA线性判别分析（转）

    线性判别分析LDA详解 1 Linear Discriminant Analysis    相较于FLD(Fisher Linear Decriminant),LDA假设:1.样本数据服从正态分布,2 ...

  5. LDA(线性判别分析，Python实现)

    源代码: #-*- coding: UTF-8 -*- from numpy import * import numpy def lda(c1,c2): #c1 第一类样本,每行是一个样本 #c2 第 ...

  6. LDA(Linear discriminate analysis)线性判别分析

    LDA 线性判别分析与Fisher算法完全不同 LDA是基于最小错误贝叶斯决策规则的. 在EMG肌电信号分析中,... 未完待续:.....

  7. 机器学习理论基础学习3.2--- Linear classification 线性分类之线性判别分析(LDA)

    在学习LDA之前,有必要将其自然语言处理领域的LDA区别开来,在自然语言处理领域, LDA是隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),是一种处理文档的主题 ...

  8. 线性判别分析 LDA

    点到判决面的距离 点\(x_0\)到决策面\(g(x)= w^Tx+w_0\)的距离:\(r={g(x)\over \|w\|}\) 广义线性判别函数 因任何非线性函数都可以通过级数展开转化为多项式函 ...

  9. 运用sklearn进行线性判别分析(LDA)代码实现

    基于sklearn的线性判别分析(LDA)代码实现 一.前言及回顾 本文记录使用sklearn库实现有监督的数据降维技术——线性判别分析(LDA).在上一篇LDA线性判别分析原理及python应用(葡 ...

随机推荐

  1. jquery中的append功能相当于剪切的作用 将原来的元素剪切走

    jquery中的append功能相当于剪切的作用 将原来的元素剪切走

  2. 【数据库_Postgresql】sql查询结果添加序号列

    ROW_NUMBER () OVER (ORDER BY A .ordernumber ASC) AS 序号

  3. 【Java】编程技术经典书籍列表

    这个列表包括了 100 多本经典技术书籍,涵盖:计算机系统与网络.系统架构.算法与数据结构.前端开发.后端开发.移动开发.数据库.测试.项目与团队.程序员职业修炼.求职面试 和 编程相关的经典书籍. ...

  4. [四]SpringBoot 之 捕捉全局异常

    在class注解上@ControllerAdvice, 在方法上注解上@ExceptionHandler(value = Exception.class),具体代码如下: package me.shi ...

  5. Innobackupx工具命令简单解析

    --defaults-file 同xtrabackup的--defaults-file参数,指定mysql配置文件; --apply-log 对xtrabackup的--prepare参数的封装; - ...

  6. P1054 等价表达式

    题目描述 明明进了中学之后,学到了代数表达式.有一天,他碰到一个很麻烦的选择题.这个题目的题干中首先给出了一个代数表达式,然后列出了若干选项,每个选项也是一个代数表达式,题目的要求是判断选项中哪些代数 ...

  7. 转：评估指标MAP

    转:http://www.zhenv5.com/?p=1079 MAP可以由它的三个部分来理解:P,AP,MAP 先说P(Precision)精度,正确率.在信息检索领域用的比较多,和正确率一块出现的 ...

  8. Sort Integers

    ) algorithm. 分析 bubble sort 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public class Solution ...

  9. day2-python基础

  10. 特征点检测学习_2(surf算法)

    依旧转载自作者:tornadomeet 出处:http://www.cnblogs.com/tornadomeet 特征点检测学习_2(surf算法) 在上篇博客特征点检测学习_1(sift算法) 中 ...