sklearn学习一

转发说明：by majunman    from HIT    email:2192483210@qq.com

简介：scikit-learn是数据挖掘和数据分析的有效工具，它建立在 NumPy, SciPy, and matplotlib基础上。开源的但商业不允许

1. Supervised learning

1.1. Generalized Linear Models

1.1.1. Ordinary Least Squares最小二乘法

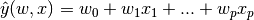
>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> reg.coef_
array([ 0.5,  0.5])

reg-http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression

reg.coef_   是回归函数的结果，即相关系数

具体实验：

print(__doc__)
 
# Code source: Jaques Grobler
# License: BSD 3 clause
 
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
 
# Load the diabetes dataset
diabetes = datasets.load_diabetes()   #加载diabetes数据集（sklearn提供的几种数据集之一，该数据是糖尿病数据集）
 
# Use only one feature
diabetes_X = diabetes.data[:, np.newaxis, 2]   #只加载一个特征值
 
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
 
# Split the targets into training/testing sets
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]
 
# Create linear regression object
regr = linear_model.LinearRegression()
 
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
 
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
 
# The coefficients
print('Coefficients: \n', regr.coef_)
# The mean squared error
print("Mean squared error: %.2f"
      % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
 
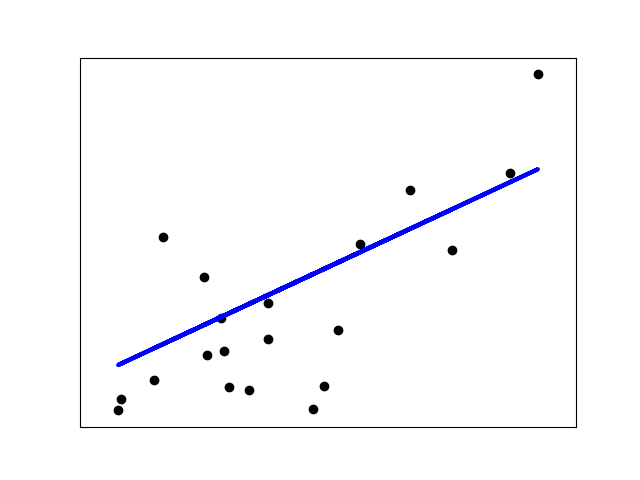
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
 
plt.xticks(())
plt.yticks(())
 
plt.show()