Parameter Initializations in Deep Learning
全零初始化的问题:
在Linear Regression中,常用的参数初始化方式是全零,因为在做Gradient Descent的时候,各个参数会在输入的各个分量维度上各自更新。更新公式为:

而在Neural Network(Deep Learning)中,当我们将所有的parameters做全零初始化,根据公式:

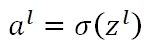
可知,每一层的Zl均为0,如果使用sigmoid activation,则al的值都等于0.5。在反向传播时,误差值
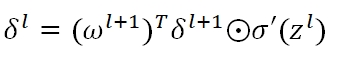
因为有ω在里面,所以导致δ都变成了零,而我们用于做Gradient Descent的梯度
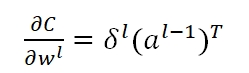
也就通通变为了零,从而,我们的Back propagation算法失效,参数矩阵将始终保持全零的状态,无法更新。
Parameter初始化过小的问题:
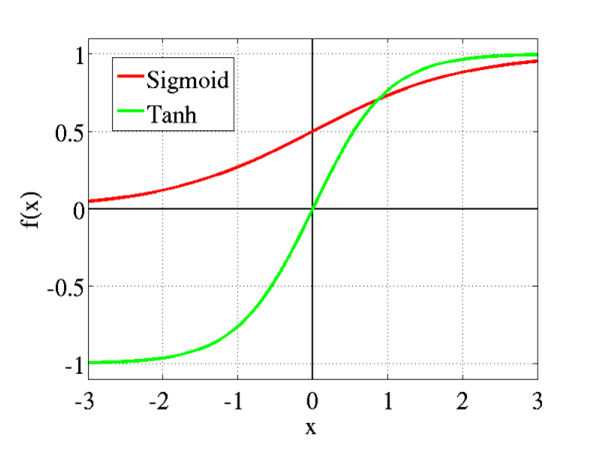
首先,Parameter过小,则经过一层层的Sigmoid Function,activation会越来越小,也就是最终的输出结果会非常接近于0。从Sigmoid的图形可以看出,在接近0的图形范围内,函数是类似线性的。所以Parameter初始化过小,会导致神经网络失去非线性功能。此外,在接近0点的部分,Sigmoid Activation的δ'(z)接近于1/4。同样地,在公式中:
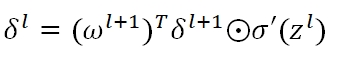
随着Backpropagation的进行,δ指数级衰减。下式中的梯度会随着层数的回溯,越来越小,直至消失消失。
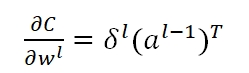
Parameter初始化过大的问题:
将导致Z值过大,从Sigmoid和Tanh图形可知,当Z值过大时,激励函数会饱和,其梯度将趋近为0。导致的结果是,参数将无法进行更新,或更新很慢。
而如果我们通过调整bias,使得各层的z始终为0,则会有梯度爆炸的问题。还是在下式中
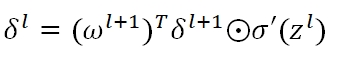
各层的δ‘(z)都是1/4,但ω却是很大的值。所以随着Backpropagation的推进,前层的δ会越来越大,如果层数很多,甚至变为NAN。
深度学习中的主流初始化方法有Xavier和He
Xavier Initialization有三种选择,Fan_in:

Fan_out:
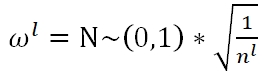
Average:
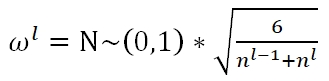
He Initialization:
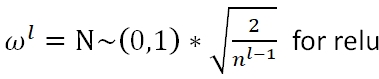
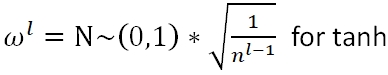
Parameter Initializations in Deep Learning的更多相关文章
- Decision Boundaries for Deep Learning and other Machine Learning classifiers
Decision Boundaries for Deep Learning and other Machine Learning classifiers H2O, one of the leading ...
- Edge Intelligence: On-Demand Deep Learning Model Co-Inference with Device-Edge Synergy
边缘智能:按需深度学习模型和设备边缘协同的共同推理 本文为SIGCOMM 2018 Workshop (Mobile Edge Communications, MECOMM)论文. 笔者翻译了该论文. ...
- A Brief Overview of Deep Learning
A Brief Overview of Deep Learning (This is a guest post by Ilya Sutskever on the intuition behind de ...
- Rolling in the Deep (Learning)
Rolling in the Deep (Learning) Deep Learning has been getting a lot of press lately, and is one of t ...
- 深度学习Deep learning
In the last chapter we learned that deep neural networks are often much harder to train than shallow ...
- Deep learning:五十一(CNN的反向求导及练习)
前言: CNN作为DL中最成功的模型之一,有必要对其更进一步研究它.虽然在前面的博文Stacked CNN简单介绍中有大概介绍过CNN的使用,不过那是有个前提的:CNN中的参数必须已提前学习好.而本文 ...
- Deep Learning 19_深度学习UFLDL教程:Convolutional Neural Network_Exercise(斯坦福大学深度学习教程)
理论知识:Optimization: Stochastic Gradient Descent和Convolutional Neural Network CNN卷积神经网络推导和实现.Deep lear ...
- Deep Learning in a Nutshell: History and Training
Deep Learning in a Nutshell: History and Training This series of blog posts aims to provide an intui ...
- Deep Learning 13_深度学习UFLDL教程:Independent Component Analysis_Exercise(斯坦福大学深度学习教程)
前言 理论知识:UFLDL教程.Deep learning:三十三(ICA模型).Deep learning:三十九(ICA模型练习) 实验环境:win7, matlab2015b,16G内存,2T机 ...
随机推荐
- Djaon 基于 Ajax 的 json 数据传输
关键参数:contentType:"application/json" data:JSON.stringify({ json数据 }) 再views.py中,使用request.d ...
- Runnable和Thread区别和比较
在很多博客中用这样一个例子来说明 Runnable更容易实现资源共享,能多个线程同时处理一个资源. 看代码: public static void main(String[] args) { new ...
- R语言常用数据管理
1.变量的重命名 (1)交互式编辑器修改变量名 若要修改数据集x中的变量名,键入fix(x)即可打开交互式编辑器的界面.若数据集为矩阵或数据框,单击交互式编辑器界面中对应要修改的变量名,可手动输入新的 ...
- 帝国CMS链接域名重写、伪静态处理
需求:将 www.abc.com/e/tags?tagsid=1 改写成 www.abc.com/softlink/1.html形式: 环境:Windows服务器: 路径:D:/web/www.ab ...
- [翻译]解释JavaScript中的类型转换
原文地址:JavaScript type coercion explained 类型转换是将值从一种类型转换为另一种类型的过程(比如字符串转换为数值,对象转换为布尔值,等等).任何类型,无论是原始类型 ...
- .NetCore模拟Postman的BasicAuth生成Authrization
一.思路 BasicAuth 是一种简单权限,传输UserName=<userName>,Password=<password> 1.用:连接Username,Password ...
- netcore中使用session
- 四、MyBatis-映射文件
映射文件指导着MyBatis如何进行数据库增删改查,有着非常重要的意义. <?xml version="1.0" encoding="UTF-8" ?&g ...
- bzoj4408 [Fjoi 2016]神秘数 & bzoj4299 Codechef FRBSUM 主席树+二分+贪心
题目传送门 https://lydsy.com/JudgeOnline/problem.php?id=4299 https://lydsy.com/JudgeOnline/problem.php?id ...
- java 关键字volatile
一.Java内存模型 想要理解volatile为什么能确保可见性,就要先理解Java中的内存模型是什么样的. Java内存模型规定了所有的变量都存储在主内存中.每条线程中还有自己的工作内存,线程的工作 ...
