二叉平衡树AVL的插入与删除(java实现)

二叉平衡树

全图基础解释参考链接：http://btechsmartclass.com/data_structures/avl-trees.html

二叉平衡树：https://www.cnblogs.com/zhuwbox/p/3636783.html

前提：会写 求二叉树的深度

背景知识：

为什么需要二叉平衡树

答：因为二叉搜索树在理想状态下（也就是平衡树），查找的时间复杂度为log2n ,但是如果很不幸，

​ 插入的数据都是有序数据的话，那么会退化成O(n)的线性时间复杂度。因为几乎退化成了链！

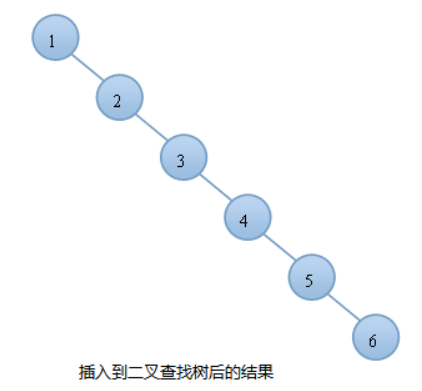
线性：6次

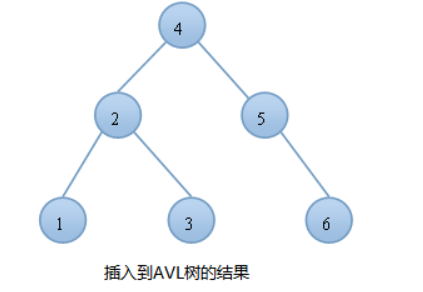
平衡：3次 log6+1 = 3

总结：树的基本操作的时间复杂度几乎都与树的高度有关，那么减少树的高度，就可以降低查询的时间复杂度。

　我们知道，对于一般的二叉搜索树（Binary Search Tree），其期望高度（即为一棵平衡树时）为log2n，其各操作的时间复杂度（O(log2n)）同时也由此而决定。但是，在某些极端的情况下（如在插入的序列是有序的时），二叉搜索树将退化成近似链或链，此时，其操作的时间复杂度将退化成线性的，即O(n)。我们可以通过随机化建立二叉搜索树来尽量的避免这种情况，但是在进行了多次的操作之后，由于在删除时，我们总是选择将待删除节点的后继代替它本身，这样就会造成总是右边的节点数目减少，以至于树向左偏沉。这同时也会造成树的平衡性受到破坏，提高它的操作的时间复杂度。

　　例如：我们按顺序将一组数据1,2,3,4,5,6分别插入到一颗空二叉查找树和AVL树中，插入的结果如下图：

　　　　　　　　

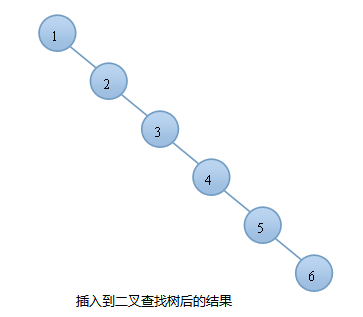
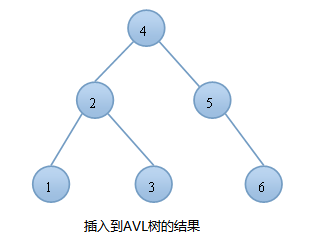
AVL树的插入

　　由上图可知，同样的结点，由于插入方式不同导致树的高度也有所不同。特别是在带插入结点个数很多且正序的情况下，会导致二叉树的高度是O(N)，而AVL树就不会出现这种情况，树的高度始终是O(lgN).高度越小，对树的一些基本操作的时间复杂度就会越小。这也就是我们引入AVL树的原因

　　AVL树的操作基本和二叉查找树一样，这里我们关注的是两个变化很大的操作：插入和删除！

　　我们知道，AVL树不仅是一颗二叉查找树，它还有其他的性质。如果我们按照一般的二叉查找树的插入方式可能会破坏AVL树的平衡性。同理，在删除的时候也有可能会破坏树的平衡性，所以我们要做一些特殊的处理，包括：单旋转和双旋转！

　　AVL树的插入，单旋转的第一种情况---右旋：

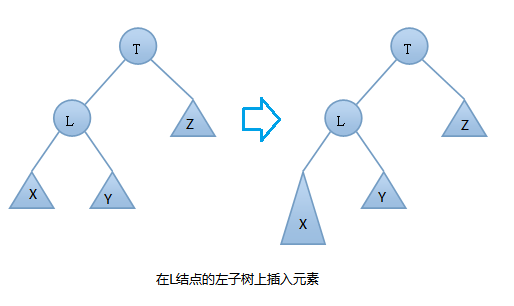
　　由上图可知：在插入之前树是一颗AVL树，而插入之后结点T的左右子树高度差的绝对值不再 < 1,此时AVL树的平衡性被破坏，我们要对其进行旋转。由上图可知我们是在结点T的左结点的左子树上做了插入元素的操作，我们称这种情况为左左情况，我们应该进行右旋转(只需旋转一次，故是单旋转)。具体旋转步骤是：

　　T向右旋转成为L的右结点，同时，Y放到T的左孩子上。这样即可得到一颗新的AVL树，旋转过程图如下：

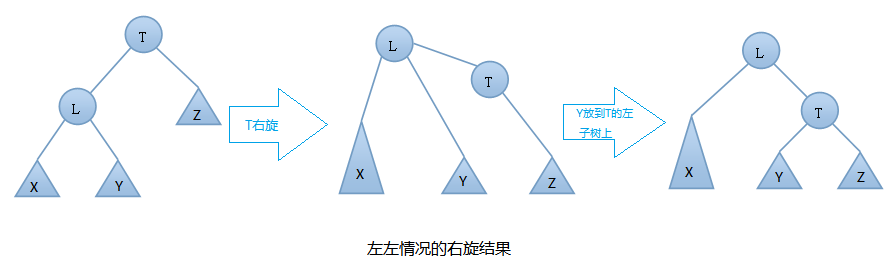
　　左左情况的右旋举例：

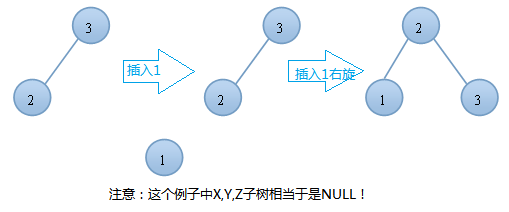
　　AVL树的插入，单旋转的第一种情况---左旋：

　

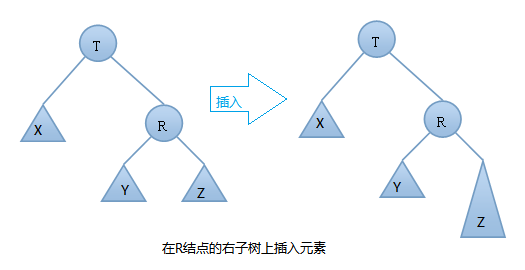
　　　由上图可知：在插入之前树是一颗AVL树，而插入之后结点T的左右子树高度差的绝对值不再 < 1,此时AVL树的平衡性被破坏，我们要对其进行旋转。由上图可知我们是在结点T的右结点的右子树上做了插入元素的操作，我们称这种情况为右右情况，我们应该进行左旋转(只需旋转一次，故事单旋转)。具体旋转步骤是：

　　　T向右旋转成为R的左结点，同时，Y放到T的左孩子上。这样即可得到一颗新的AVL树，旋转过程图如下：

　

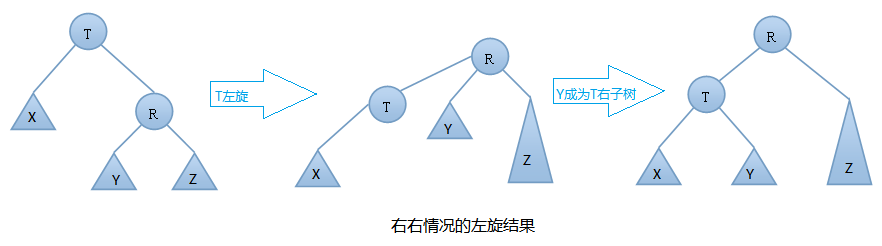
　　右右情况的左旋举例：

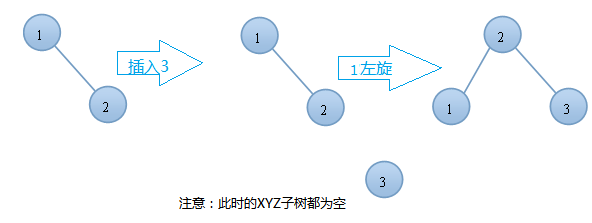
　　以上就是插入操作时的单旋转情况！我们要注意的是：谁是T谁是L，谁是R还有谁是X,Y,Z!T始终是开始不平衡的左右子树的根节点。显然L是T的左结点，R是T的右节点。X、Y、Y是子树当然也可以为NULL.NULL归NULL，但不能破坏插入时我上面所说的左左情况或者右右情况。

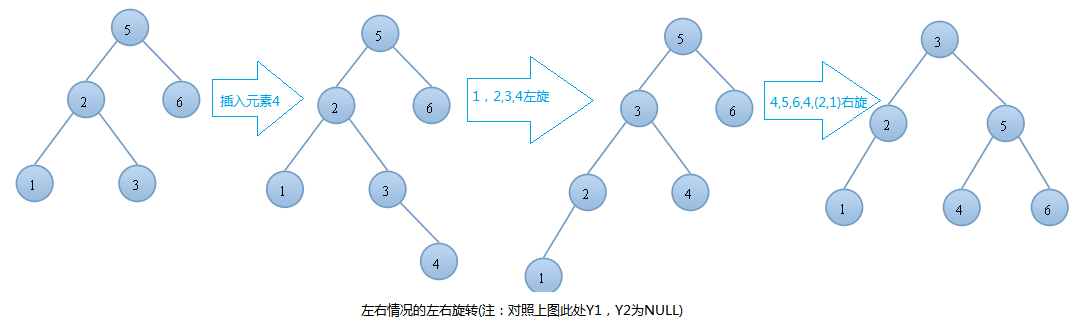
　　AVL树的插入，双旋转的第一种情况---左右(先左后右)旋：

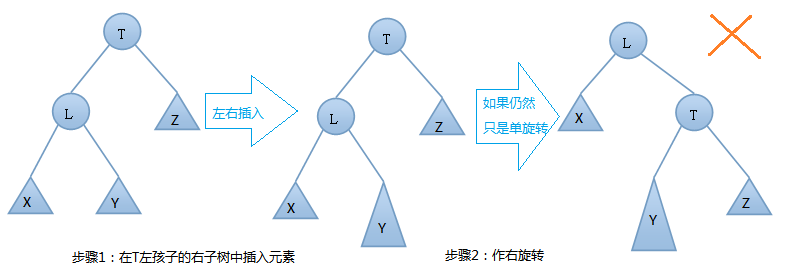
由　　上图可知，我们在T结点的左结点的右子树上插入一个元素时，会使得根为T的树的左右子树高度差的绝对值不再 < 1，如果只是进行简单的右旋，得到的树仍然是不平衡的。我们应该按照如下图所示进行二次旋转：

　　

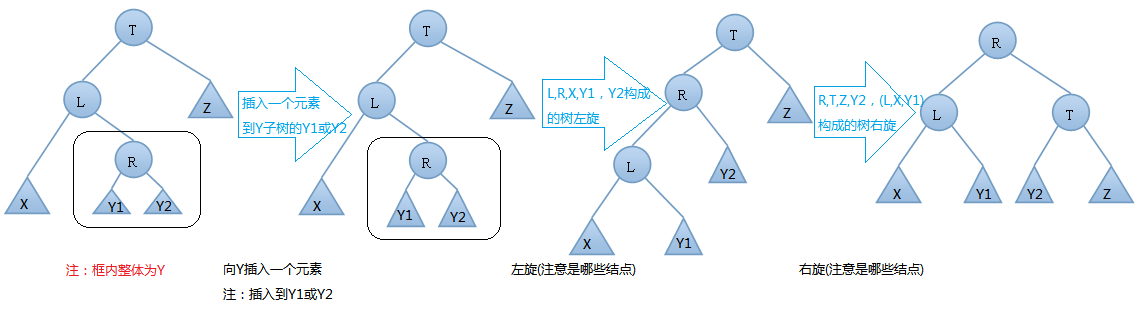
　　左右情况的左右旋转实例：

　　AVL树的插入，双旋转的第二种情况---右左(先右后左)旋：

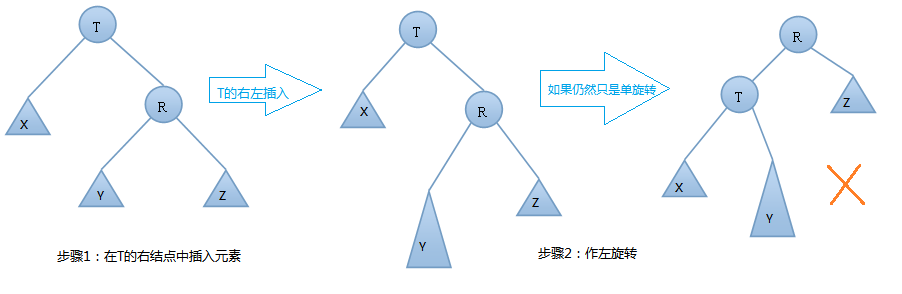
　　由上图可知，我们在T结点的右结点的左子树上插入一个元素时，会使得根为T的树的左右子树高度差的绝对值不再 < 1，如果只是进行简单的左旋，得到的树仍然是不平衡的。我们应该按照如下图所示进行二次旋转：

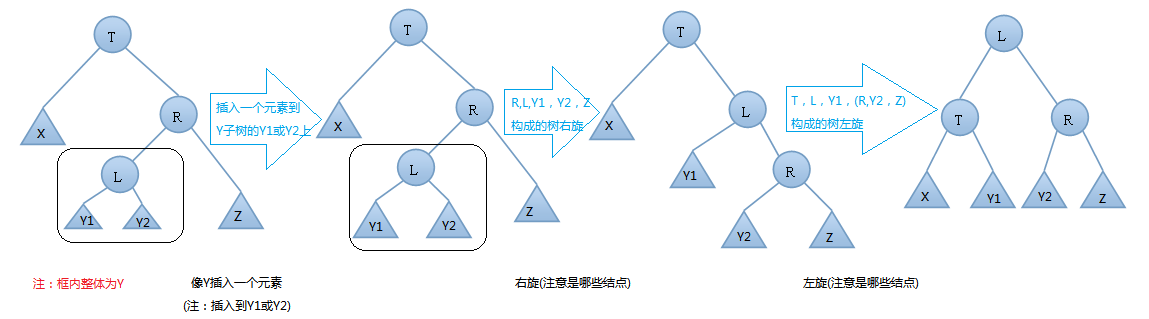
　　右左情况的右左旋转实例：

插入代码：

    /**
     * 插入结点 (测试整形插入)
     */
    public AVLNode<T> insertNode(AVLNode T,T value){
        if(T==null){
            T = new AVLNode(value);
        }else{
            //走左边
            if((Integer)value<(Integer)T.data){
                T.lchild = insertNode(T.lchild,value);
                //分情况旋转

                //判断是否需要旋转
                if(getHeight(T.lchild)-getHeight(T.rchild)>=2){
                    //左左情况
                    if((Integer)value<(Integer)T.lchild.data){  //这是针对插入会出现的情况判断（也可以通过比较孩子结点的当前高度来判断）
//                       if(getHeight(T.lchild)>getHeight(T.rchild)){
                        //单旋-右旋
                        T =  singleRotateWithRight(T);
                    }else{
                        //左右情况 (排除掉相同的元素，相同元素不允许再次插入)

                        //先左转，再右转 LR
                        T = doubleRotateWithLeft(T);
                    }
                }

                //走右边
            }else if((Integer)value>(Integer)T.data){
                T.rchild = insertNode(T.rchild,value);

                //分情况旋转
                if(getHeight(T.rchild)-getHeight(T.lchild)>=2){
                    //右右情况
                    if((Integer)value>(Integer)T.rchild.data){ //这是针对插入会出现的情况判断（也可以通过比较孩子结点的当前高度来判断）
//                      if(getHeight(T.rchild)>getHeight(T.lchild)){
                        //单旋-左旋
                        T = singleRotateWithLeft(T);
                    }else{
                        //右左情况
                        T = doubleRotateWithRight(T);
                    }
                }
            }else{
                //相同，不再进行插入
            }
        }

        //每次插入都要 计算高度，这个高度是递归式的!
        T.height = Max(getHeight(T.lchild),getHeight(T.rchild))+1; //每一层递归结束之前要重新计算一下高度（因为可能插入了新结点）
        return T;
    }

AVL树的删除操作

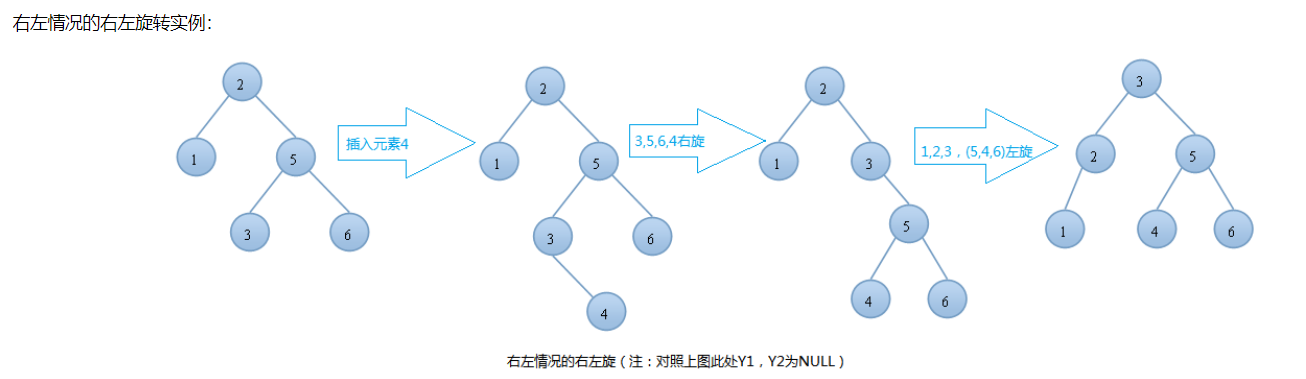
分析：我们用插入的例子来分析删除操作

1. 首先，如果要删除的结点比当前根节点大，那么就会走左边进去

2. 走左边进去删除后，判断是否需要平衡的依据一定是：

   if(getHeight(T.rchild)-getHeight(T.lchild)>=2) //删掉左子树的孩子结点，肯定是右边可能会高过左边的情况
   

3. 然后如果需要重新平衡(修复)，那么要进行哪种修复呢

   观察图：知道如果删除的是左边的结点，那么会出现：LL或者RL这样的旋转

   RL：如果删除了左边结点的，出现了根节点2 的平衡因子从-1 变到了-2，那么再判断：根的右子树5的

   左子树和右子树的高度差，当T.rchild.lchild.height >T.rchild.rchild.height，即满足上面需要RL旋转的的情况

                   if(getHeight(T.rchild)-getHeight(T.lchild)>=2){
                       //删掉左子树的孩子结点，肯定是右边可能会高过左边的情况
                       if(getHeight(T.rchild.lchild)>getHeight(T.rchild.rchild)){
                           //左子树的 右子树比左子树的左子树要高
                           //RL旋转
                           T = doubleRotateWithRight(T);
                           //记住，因为旋转后，根节点会发生变化，一定要重新接收根结点
                       }else{
                           //RR
                           T = singleRotateWithLeft(T);
                       }
                   }
   

   所有代码：

       /**
        * 删除操作
        */
       public AVLNode<T> deleteNode(AVLNode T,T value){
           if(T==null){
               return null;
           }else{
               //往左走
               if((Integer)value<(Integer) T.data){
                   T.lchild = deleteNode(T.lchild,value);  //函数返回新的根节点（所以要重新建立孩子与双亲间的联系）
                   if(getHeight(T.rchild)-getHeight(T.lchild)>=2){ //删掉左子树的孩子结点，肯定是右边可能会高过左边的情况
                       if(getHeight(T.rchild.lchild)>getHeight(T.rchild.rchild)){  //左子树的 右子树比左子树的左子树要高
                           //RL旋转
                           T = doubleRotateWithRight(T);    //记住，因为旋转后，根节点会发生变化，一定要重新接收根结点
                       }else{
                           //RR
                           T = singleRotateWithLeft(T);
                       }
                   }
                   //往右走
               }else if((Integer)value>(Integer)T.data){
                   T.rchild = deleteNode(T.rchild,value);
                   if(getHeight(T.lchild)-getHeight(T.rchild)>=2){   //删掉右子树的孩子结点，肯定是左边可能会高过右边的情况
                       if(getHeight(T.lchild.rchild)>getHeight(T.lchild.lchild)){
                           //LR旋转
                           T = doubleRotateWithLeft(T);
                       }else{
                           //LL
                           T = singleRotateWithRight(T);
                       }
                   }
               }else{
                   //找到了要删除的结点
   
                   //1. 没有左右孩子，删除的是叶子节点  (不用判断是否需要修复--旋转)
                   if(T.lchild==null&&T.rchild==null){
                       T = null;
                       //2. 删除的结点只有左孩子或右孩子
                   }else {
                       if(T.lchild!=null){
                           T = T.lchild;
                       }else if(T.rchild!=null){
                           T = T.rchild;
                       }else{
                           //3. 删除的结点左右孩子都有
                           T.data = find_min_value(T.rchild);  //找到最小节点，替换
                           T.rchild = deleteNode(T.rchild,(T)T.data);  //删除替换的最小的那个结点
   
                           //判断旋转
                           if(getHeight(T.lchild)-getHeight(T.rchild)>=2){
                               if(getHeight(T.lchild.rchild)-getHeight(T.lchild.lchild)>=2){
                                   //LR
                                   T = doubleRotateWithLeft(T);
                               }else{
                                   //LL
                                   T = singleRotateWithRight(T);
                               }
                           }
                       }
                   }
               }
           }
           if(T!=null){
               //重新计算高度
               T.height = Max(getHeight(T.lchild),getHeight(T.rchild))+1;
           }
   
           //返回新的根节点
           return T;
   
       }
   
       /**
        * 找到最小的结点值
        */
       public T find_min_value(AVLNode T){
   
           if(T.lchild==null){
               return (T) T.data;
           }else{
               return find_min_value(T.lchild);
           }
       }
   
       /**
        * 用于比较两棵子树高度，比较哪边高 ，用于节点高度 = Max(T.lchild.height,T.rchild.height)+1
        */
       public int Max(int lHeight,int rHeight){
           if(lHeight>=rHeight){
               return lHeight;
           }else{
               return rHeight;
           }
       }
   
       /**
        * 获取结点高度,因为可能计算高度的时候，左右孩子结点很可能为空，如果不用这个方法判断的话，会导致nullPointerException
        */
       public int getHeight(AVLNode T){
           if(T==null){
               return -1;
           }else{
               return T.height;
           }
       }
   

测试代码

        System.out.println();
        System.out.println("测试AVL：");
        //测试AVL
        AVLTree<Integer> avlTree = new AVLTree<>();

        avlTree.root = avlTree.insertNode(avlTree.root,1);
        avlTree.root = avlTree.insertNode(avlTree.root,2);
        avlTree.root = avlTree.insertNode(avlTree.root,3);
        avlTree.root = avlTree.insertNode(avlTree.root,4);
        avlTree.root = avlTree.insertNode(avlTree.root,5);
        avlTree.root = avlTree.insertNode(avlTree.root,6);
        avlTree.root = avlTree.insertNode(avlTree.root,7);
        avlTree.root = avlTree.insertNode(avlTree.root,8);
        avlTree.root = avlTree.insertNode(avlTree.root,10);
        avlTree.root = avlTree.insertNode(avlTree.root,11);
        avlTree.root = avlTree.insertNode(avlTree.root,12);
        avlTree.root = avlTree.insertNode(avlTree.root,13);
        avlTree.root = avlTree.insertNode(avlTree.root,14);
        avlTree.root = avlTree.insertNode(avlTree.root,15);

        avlTree.levelTraverse();

        System.out.println();

        System.out.println("删除5,6,7");
        avlTree.deleteNode(avlTree.root,5);
        avlTree.deleteNode(avlTree.root,7);
        avlTree.deleteNode(avlTree.root,6);

        avlTree.levelTraverse()

原来的为:

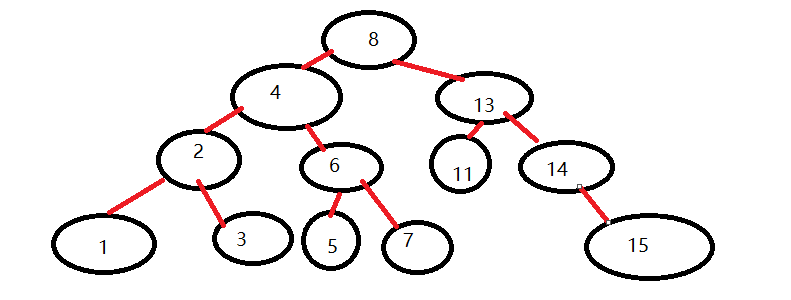
层序遍历测试结果：

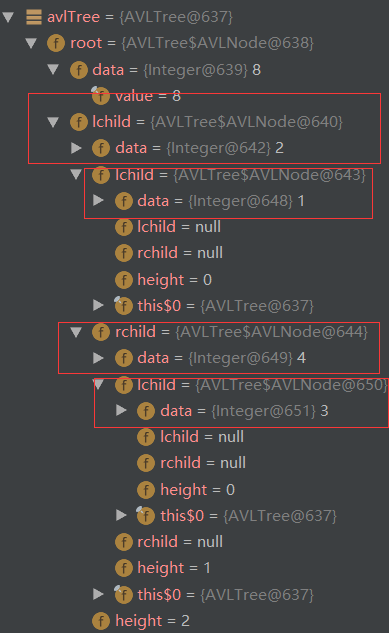
通过debug查看结果：

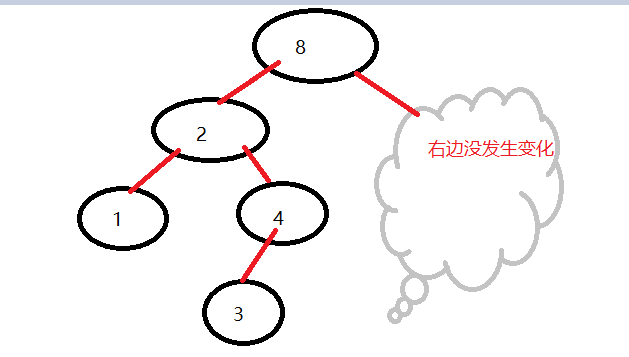
删除5,6,7后：