树状数组的理解（前缀和 and 差分）

二更——

有神仙反映数星星那个题外链炸了，我决定把图给你们粘一下，汉语翻译的话在一本通提高篇的树状数组那一章里有，同时也修改了一些汉语语法的错误

这段时间学了线段树组，当神仙们都在学kmp和hash的时候，我这个蒟蒻致远星了，，，，，所以在补完字符串算法之后我决定再补一补数据结构

这篇总结主要就是给自己看的，所以树状数组的原理请移步这篇

高赫奆佬的blogs

这篇以例题为主

首先是一道板子题

P3374 【模板】树状数组 1

这个题是个板子

让我们来看一看树状数组的一些操作

1.对某一个点添加某个值

void update(int x,int y)
{
    while(x <= n){
        t[x] += y;
        x += lowbit(x);
    }
}

考虑树状数组t[ x] 表示区间[x-lowbit(x)+1,x]之间所有数的和，又因为所有x为2的整倍数的t数组的值都来自于前面2的整倍数的贡献，所以我们要把每一个lowbit（x）都进行添加x值

如果你看不懂，可以看看这个图

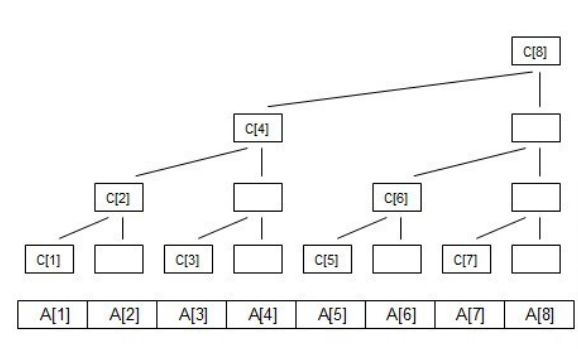
2.还有就是查询某个区间的值

我们肯定知道在前缀和中[x,y]这个区间的值就是sum(y)-sum(x-1)对吧，然后我们只需要写出来sum函数就可以了

int sum(int x)
{
    int res = ;
    while(x>){
        res += t[x];
        x -= lowbit(x);
    }
    return res;
}

还有就是快速求lowbit（x）的值的代码

int lowbit(int x)
{
    return x & (-x);
}

这样我们这道板子题就差不多完事了

放一下代码吧

#include <iostream>
#include <cstdio>
using namespace std;
int n, m, t[];
int lowbit(int x)
{
    return x & (-x);
}
void update(int x,int y)
{
    while(x <= n){
        t[x] += y;
        x += lowbit(x);
    }
}
int sum(int x)
{
    int res = ;
    while(x>){
        res += t[x];
        x -= lowbit(x);
    }
    return res;
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = , v; i <= n; ++i){
        scanf("%d", &v);
        update(i,v);
    }
    for (int i = , temp, u, v; i <= m; ++i){
        scanf("%d%d%d", &temp, &u, &v);
        if(temp == )    update(u,v);
        else    printf("%d\n",sum(v) - sum(u - ));
    }
    return ;
}

下面来看到第二个板子

P3368 【模板】树状数组 2

这个题换了一个问法，问的是某几个数的差，所以我们再添加差分这个元素

把原本p[x]表示的意思变为[x-lowbiut(x)+1,x]这个区间右端点与左端点的差，因为还是按照lowbit（x）来倍增的，所以我们能够通过sum这个函数来求得任意两个数的差分值，然后相减就能得到所求数字，不明白的话，我慢慢讲来。

首先sum和update的方法是不变的，但是因为我们对于一个区间内的所有数都加z，所以这个区间内的差分值是不变的，我们只对左端点的差分值加z，右端点+1的位置的差分值-z就行了

update(l,z);
update(r + ,-z);

想要求某一个数的话，直接将这个数到1所有的差分值相加即可求得，也就是sum（x）

这个题就完事啦

#include <iostream>
#include <cstdio>
using namespace std;
long long n, m,t[];
inline int lowbit(int x)
{
    return x & (-x);
}
inline void update(int x,int y)
{
    while(x<=n){
        t[x] += y;
        x += lowbit(x);
    }
}
inline int sum(int x)
{
    int res = ;
    while(x){
        res += t[x];
        x -= lowbit(x);
    }
    return res;
}
int main()
{
    scanf("%d%d", &n, &m);
    int now,past = ;
    for (int  i = ; i <= n; ++i){
        scanf("%d", &now);
        update(i,now - past);
        past = now;
    }
    for (int i = ,k; i <= m;++i){
        scanf("%d", &k);
        if(k == ){
            int x, y, z;
            scanf("%d%d%d", &x, &y, &z);
            update(x,z);
            update(y + ,-z);
        }
        else{
            int x;
            scanf("%d", &x);
            printf("%d\n", sum(x));
        }
    }
    return ;
}

还有一道比较好玩的题目

ural 1028 stars

这个题的大体意思就是给你星星的坐标，在星星左下方的（包括正左和正下）的星星有k颗，那么这个星星就是k级的，问每一级星星的数量，星星的坐标按照y轴升序输入，y轴相同的按x轴升序输入

怎么说呢，一看到坐标肯定先想到二维数组，但是数据范围在这个地方了，你肯定是不能开p[15000][15000]的，我们再看看这个题，他的输入很棒啊，保证了后输入的一定是把之前输入的星星包含在内了，所以我们就可以用a[x] 表示横坐标为x的星星的个数，然后跑一遍统计一下就可以辣

上代码

这地方有个坑，就是星星的坐标可以是(0,0)但是我们跑前缀和的时候因为有lowbit（x）操作，下标必须从1开始，所以我们把每一个读进来的x都++，这样的话不仅不影响最终结果，而且也不会出锅啦

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

using namespace std;

int c[];
int level[];

//求2的K次幂
int lowbit(int t)
{
    return t&(-t);
}
//更新树状数组
void update(int t)
{
    while(t<)
    {
        ++c[t];
        t+=lowbit(t);
    }
}
//获取前N项和
int getSum(int t)
{
    int sum = ;
    while(t>)
    {
        sum+=c[t];
        t-=lowbit(t);
    }
    return sum;
}
int main()
{
    int n;
    int x;
    int y;
    int i;
    int sum;

    scanf("%d",&n);

    memset(c,,sizeof(c));
    memset(level,,sizeof(c));

    for(i = ;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        ++x;//星星的左边可以从0开始，但是update函数的参数却不能是0，所有向后移一位
        update(x);
        sum = getSum(x);
        ++level[sum];
    }
    for(i = ;i<n;i++)
    {
        printf("%d\n",level[i+]);
    }
    return ;
}

ok 完事~