windows下nvm的安装及使用

由于更新了npm版本之后导致npm的命令都会报错，一顿百度，明白了nvm可以管理node版本的，下面是操作过程：

如果在安装nvm之前已经下载了node

需要把node卸载！！！

需要把node卸载！！！

需要把node卸载！！！

第一步：下载nvm

直接到https://github.com/coreybutler/nvm-windows/releases下载

nvm-noinstall.zip： 这个是绿色免安装版本，但是使用之前需要配置
nvm-setup.zip：这是一个安装包，下载之后点击安装，无需配置就可以使用，方便。
Source code(zip)：zip压缩的源码
Sourc code(tar.gz)：tar.gz的源码，一般用于*nix系统

4个选择，想方便就下载setup，我下载的是最新版1.1.7.

第二步：安装

解压下载的zip，生成nvm-setup.exe文件并运行

​

配置安装地址：

​

设置node的symlink文件夹位置。这个文件夹的名字一定不能含有中文或空格！

​

安装完成：

​

执行命令nvm，出现下面表示成功：

​

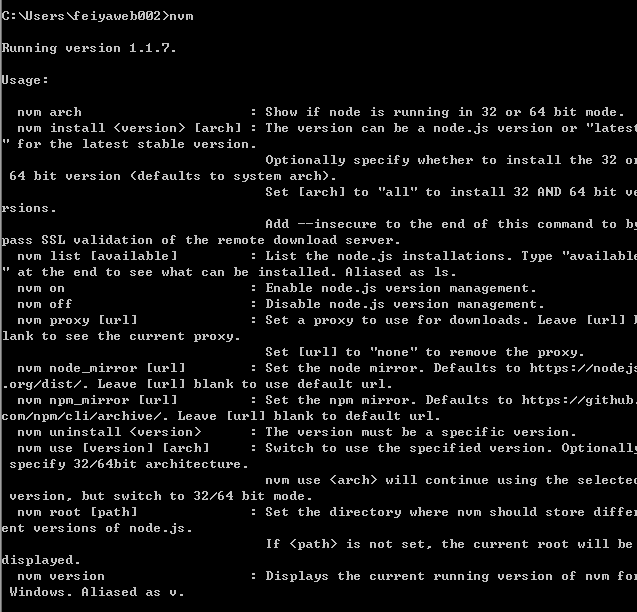
第三步：修改settings.txt

在你安装的目录下找到settings.txt文件，打开后加上

node_mirror: https://npm.taobao.org/mirrors/node/

npm_mirror: https://npm.taobao.org/mirrors/npm/

​

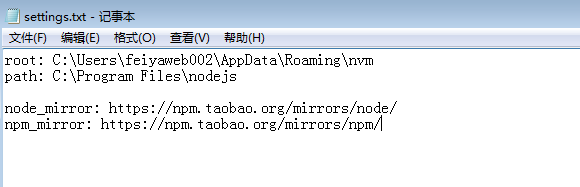
这一步主要是将npm镜像改为淘宝镜像。提高下载速度！！

第四步：使用

• nvm arch [32|64]： 显示node是运行在32位还是64位模式。指定32或64来覆盖默认体系结构。
• -nvm install <version> [arch]：该可以是node.js版本或最新稳定版本latest。（可选[arch]）指定安装32位或64位版本（默认为系统arch）。设置[arch]为all以安装32和64位版本。在命令后面添加–insecure，可以绕过远端下载服务器的SSL验证。
• nvm list [available]：列出已经安装的node.js版本。可选的available，显示可下载版本的部分列表。这个命令可以简写为nvm ls [available]。
• nvm on： 启用node.js版本管理。
• nvm off： 禁用node.js版本管理(不卸载任何东西)
• nvm proxy [url]： 设置用于下载的代理。留[url]空白，以查看当前的代理。设置[url]为none删除代理。
• nvm node_mirror [url]：设置node镜像，默认为https://nodejs.org/dist/.。可以设置为淘宝的镜像https://npm.taobao.org/mirrors/node/
• nvm npm_mirror [url]：设置npm镜像，默认为https://github.com/npm/npm/archive/。可以设置为淘宝的镜像https://npm.taobao.org/mirrors/npm/
• nvm uninstall <version>： 卸载指定版本的nodejs。
• nvm use [version] [arch]： 切换到使用指定的nodejs版本。可以指定32/64位[arch]。
• -nvm use <arch>：将继续使用所选版本，但根据提供的值切换到32/64位模式
• nvm root [path]： 设置 nvm 存储node.js不同版本的目录 ,如果未设置，将使用当前目录。
• -nvm version： 显示当前运行的nvm版本，可以简写为nvm v

我的步骤：

​

到这里就差不多完成了，如果要下载呗的版本执行nvm list available

​

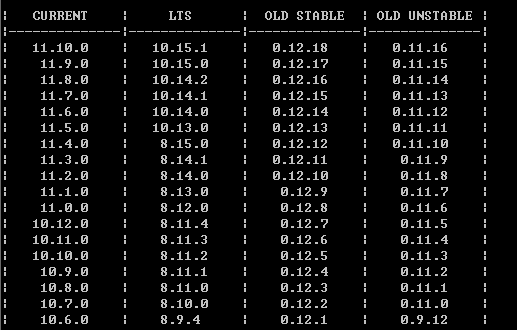
输入 npm install ***就可以下载需要的版本了，然后nvm use ***就ok了，最后执行nvm list 带*的就是选中的版本