6389. 【NOIP2019模拟2019.10.26】小w学图论
题目描述
题解
之前做过一次
假设图建好了,设g[i]表示i->j(i<j)的个数
那么ans=∏(n-g[i]),因为连出去的必定会构成一个完全图,颜色互不相同
从n~1染色,点i的方案数是(n-g[i])
用线段树合并维护集合即可
code
#include <algorithm>#include <iostream>#include <cstdlib>#include <cstring>#include <cstdio>#define fo(a,b,c) for (a=b; a<=c; a++)#define fd(a,b,c) for (a=b; a>=c; a--)#define min(a,b) (a<b?a:b)#define mod 998244353using namespace std;int tr[4000001][4];int n,m,i,j,k,l,x,y,len;long long ans,sum;void swap(int &x,int &y){int z=x;x=y;y=z;}void New(int t,int x){if (!tr[t][x]){tr[t][x]=++len;tr[len][3]=n+1;}}void change(int t,int l,int r,int x){int mid=(l+r)/2;++tr[t][2];tr[t][3]=min(tr[t][3],x);if (l==r)return;if (x<=mid){New(t,0);change(tr[t][0],l,mid,x);}else{New(t,1);change(tr[t][1],mid+1,r,x);}}int find(int t,int l,int r,int x,int y){int sum=0,mid=(l+r)/2;if (x<=l && r<=y)return tr[t][2];if (x<=mid){if (tr[t][0])sum+=find(tr[t][0],l,mid,x,y);}if (mid<y){if (tr[t][1])sum+=find(tr[t][1],mid+1,r,x,y);}return sum;}int Find(int t,int l,int r,int x){int mid=(l+r)/2,ans=n+1,s;if (x<=l) return tr[t][3];if (tr[t][0] && x<=mid)s=Find(tr[t][0],l,mid,x),ans=min(ans,s);if (tr[t][1])s=Find(tr[t][1],mid+1,r,x),ans=min(ans,s);return ans;}void merge(int t1,int t2,int l,int r){int mid=(l+r)/2;if (l==r) return;if (tr[t1][0] && tr[t2][0])merge(tr[t1][0],tr[t2][0],l,mid);elseif (tr[t2][0])tr[t1][0]=tr[t2][0];if (tr[t1][1] && tr[t2][1])merge(tr[t1][1],tr[t2][1],mid+1,r);elseif (tr[t2][1])tr[t1][1]=tr[t2][1];tr[t1][2]=tr[tr[t1][0]][2]+tr[tr[t1][1]][2];tr[t1][3]=min(tr[tr[t1][0]][3],tr[tr[t1][1]][3]);}int main(){freopen("graph.in","r",stdin);freopen("graph.out","w",stdout);scanf("%d%d",&n,&m);len=n;fo(i,1,n)tr[i][3]=n+1;fo(i,1,m){scanf("%d%d",&x,&y);if (x>y) swap(x,y);change(x,1,n,y);}tr[0][3]=n+1;ans=n;fo(i,1,n-1){ans=(ans*(n-find(i,1,n,i+1,n)))%mod;j=Find(i,1,n,i+1);if (j<=n)merge(j,i,1,n);}printf("%lld\n",ans);fclose(stdin);fclose(stdout);return 0;}
6389. 【NOIP2019模拟2019.10.26】小w学图论的更多相关文章
- 6392. 【NOIP2019模拟2019.10.26】僵尸
题目描述 题解 吼题但题解怎么这么迷 考虑一种和题解不同的做法(理解) 先把僵尸离散化,h相同的钦(ying)点一个大小 (可以发现这样每种情况只会被算正好一次) 计算完全被占领的方案,然后1-方案/ ...
- 【JZOJ6389】小w学图论
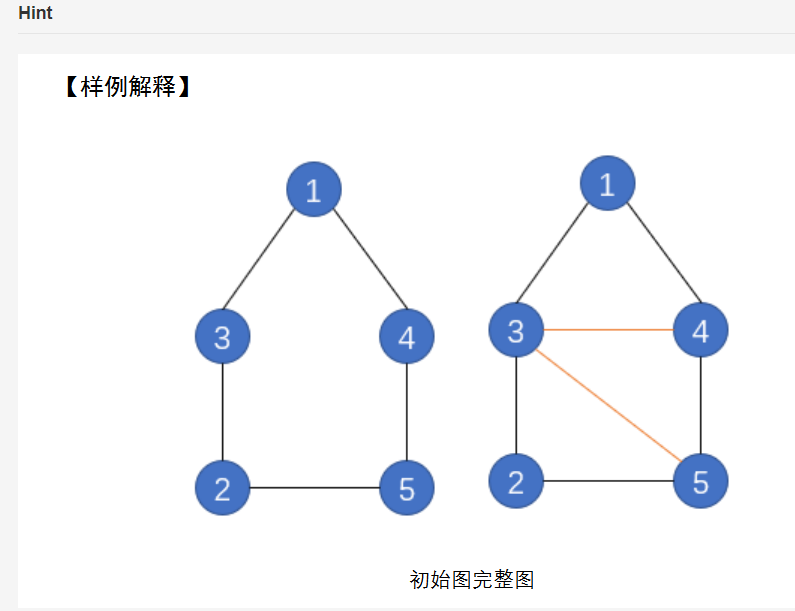
description 小w这学期选了门图论课,他在学习点着色的知识.他现在得到了一张无向图,并希望在这张图上使用最多n种颜色给每个节点染色,使得任意一条边关联的两个节点颜色不同. 小w获得一张n个节 ...
- 6380. 【NOIP2019模拟2019.10.06】小w与最长路(path)
题目 题目大意 给你一棵树,对于每一条边,求删去这条边之后,再用一条边(自己定)连接两个连通块,形成的树的直径最小是多少. 正解 首先,将这棵树的直径给找出来.显然,如果删去的边不在直径上,那么答案就 ...
- 【NOIP2019模拟2019.10.07】果实摘取 (约瑟夫环、Mobius反演、类欧、Stern-Brocot Tree)
Description: 小 D 的家门口有一片果树林,果树上果实成熟了,小 D 想要摘下它们. 为了便于描述问题,我们假设小 D 的家在二维平面上的 (0, 0) 点,所有坐标范围的绝对值不超过 N ...
- 6377. 【NOIP2019模拟2019.10.05】幽曲[埋骨于弘川]
题目描述 题解 随便bb 详细题解见 https://www.cnblogs.com/coldchair/p/11624979.html https://blog.csdn.net/alan_cty/ ...
- 6383. 【NOIP2019模拟2019.10.07】果实摘取
题目 题目大意 给你一个由整点组成的矩形,坐标绝对值范围小于等于\(n\),你在\((0,0)\),一开始面向\((1,0)\),每次转到后面第\(k\)个你能看到的点,然后将这条线上的点全部标记删除 ...
- 6374. 【NOIP2019模拟2019.10.04】结界[生与死的境界]
题目 题目大意 给你一个数列,每次可以选择任意两个相邻的数\(x\)和\(y\),将其删去,并在原来位置插入\(x+2y\). 每次询问一个区间,对这个区间进行上述操作.求最后剩下的数最大是多少. 答 ...
- UESTC_小panpan学图论 2015 UESTC Training for Graph Theory<Problem J>
J - 小panpan学图论 Time Limit: 3000/1000MS (Java/Others) Memory Limit: 65535/65535KB (Java/Others) S ...
- 【NOIP2017模拟6.25】小W的动漫
题目 小W最近迷上了日本动漫,每天都有无数部动漫的更新等着他去看,所以他必须将所有的动漫排个顺序,当然,虽然有无数部动漫,但除了1号动漫,每部动漫都有且仅有一部动漫是它的前传(父亲),也就是说,所有的 ...
随机推荐
- Java ——运算符
本节重点思维导图 递增递减 前缀自增自减法(++a,--a): 先进行自增.减运算,再进行表达式运算 后缀自增自减法(a++,a--): 先进行表达式运算,再进行自增.减运算 例[1]: int a ...
- 第九周课程总结&实验报告7
实验任务详情: 完成火车站售票程序的模拟.要求:(1)总票数1000张:(2)10个窗口同时开始卖票:(3)卖票过程延时1秒钟:(4)不能出现一票多卖或卖出负数号票的情况. 实验代码: package ...
- MySQL索引,备份和还原
1.索引 1.索引是占硬盘空间 ,也是按页存放的 . 思考题:一个索引页,(数据页) 占用多少个字节 .SQL Server 8192个字节 2.索引:是一种有效组合数据的方式,为了快速查找指定 ...
- iview报错[Vue warn]: Error in render: "TypeError: ctx.injections.tableRoot.$scopedSlots[ctx.props.column.slot] is not a function"
原因是我使用了iview的<Table>组件,我给Table组件的columns中定义了4个含有slot的列,但是实际在<Table>中只使用了其中3个,导致的报错. 也就是说 ...
- 【学习总结】快速上手Linux玩转典型应用-第4章-准备工作
课程目录链接 快速上手Linux玩转典型应用-目录 目录 1. 准备工作一 2. 准备工作二 ===================================================== ...
- NLP 中任务及相关概念
命名实体识别 命名实体识别(Named Entity Recognition,简称NER),又称作"专名识别",是指识别文本中具有特定意义的实体,主要包括人名.地名.机构名.专有名 ...
- Linux架构之Nginx之HTTPS
第52章 Nginx之HTTPS 第52章 Nginx之HTTPS 1.HTTPS安全证书基本概述 1.1 模拟服务器篡改内容 1.1.1 配置目标网站nginx 1.1.2 配置网页 1.1.3 访 ...
- Myabtis中批量更新update多字段
在mybatis中批量更新多个字段 推荐使用如下操作: 方式1:在Dao层接口中: void updateBatch(@Param("list")List<Student&g ...
- 欧拉降幂公式 Super A^B mod C
Description Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=100000 ...
- qt配置opengl
cmake 编译opengl,参考https://wiki.qt.io/How_to_setup_Qt_and_openCV_on_Windows cmake configure完成没有错误后,点击g ...
