honoka和格点三角形
题目:
她认为,满足以下三个条件的三角形是“好三角形”。
1.三角形的三个顶点均为格点,即横坐标和纵坐标均为整数。
2.三角形的面积为
3.三角形至少有一条边和
honoka想知道,在平面中选取一个大小为
分两种情况讨论:
第一种情况:
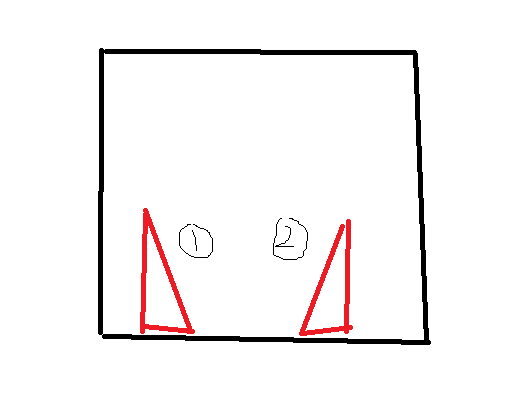
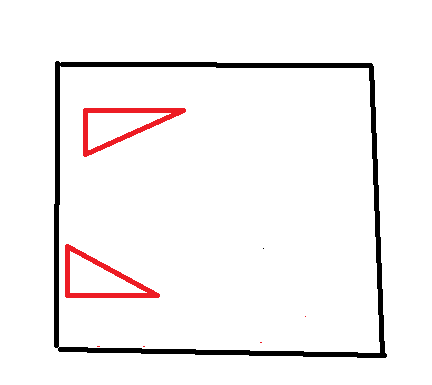
第二种情况:
①对于底边为2,高为1
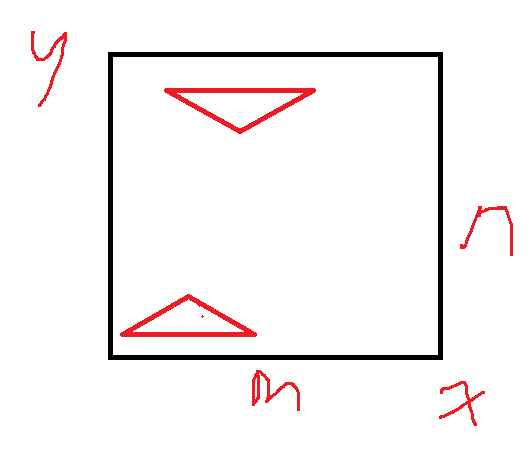
若底边和x轴平行,那么底边在x方向上有 m−2 种可能,顶点在x方向上也有 m−2(顶点的位置一共有m个,减去第一种情况中的两种)种可能,在y方向上有 n-1 种可能;
故共有2*(m-2)*(m-2)*(n-1)
若底边和y轴平行,同理可推出2*(n-2)*(n-2)*(m-1)
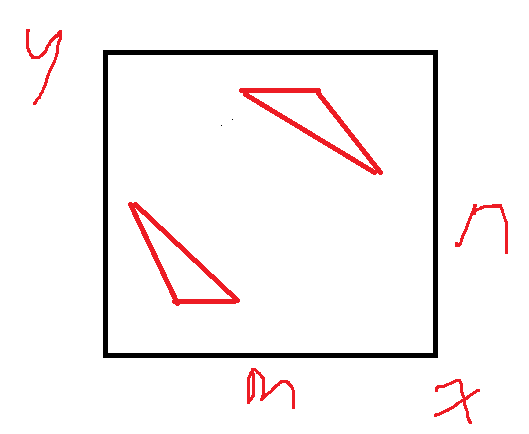
代码:
1 #include <map>
2 #include <set>
3 #include <list>
4 #include <stack>
5 #include <queue>
6 #include <deque>
7 #include <cmath>
8 #include <ctime>
9 #include <string>
10 #include <limits>
11 #include <cstdio>
12 #include <vector>
13 #include <iomanip>
14 #include <cstdlib>
15 #include <cstring>
16 #include <istream>
17 #include <iostream>
18 #include <algorithm>
19 #define ci cin
20 #define co cout
21 #define el endl
22 #define Scc(c) scanf("%c",&c)
23 #define Scs(s) scanf("%s",s)
24 #define Sci(x) scanf("%d",&x)
25 #define Sci2(x, y) scanf("%d%d",&x,&y)
26 #define Sci3(x, y, z) scanf("%d%d%d",&x,&y,&z)
27 #define Scl(x) scanf("%I64d",&x)
28 #define Scl2(x, y) scanf("%I64d%I64d",&x,&y)
29 #define Scl3(x, y, z) scanf("%I64d%I64d%I64d",&x,&y,&z)
30 #define Pri(x) printf("%d\n",x)
31 #define Prl(x) printf("%I64d\n",x)
32 #define Prc(c) printf("%c\n",c)
33 #define Prs(s) printf("%s\n",s)
34 #define For(i,x,y) for(int i=x;i<y;i++)
35 #define For_(i,x,y) for(int i=x;i<=y;i++)
36 #define FFor(i,x,y) for(int i=x;i>y;i--)
37 #define FFor_(i,x,y) for(int i=x;i>=y;i--)
38 #define Mem(f, x) memset(f,x,sizeof(f))
39 #define LL long long
40 #define ULL unsigned long long
41 #define MAXSIZE 100005
42 #define INF 0x3f3f3f3f
43
44 const int mod=1e9+7;
45 const double PI = acos(-1.0);
46
47 using namespace std;
48
49 int main(){
50 LL n,m;
51 //Sci2(n,m);
52 ci>>n>>m;
53 LL sum=(n-2)*(m-1)*4%mod+(n-1)*(m-2)*4%mod;
54 sum=(sum+2*(n-1)*(m-2)%mod*(m-2)%mod+2*(m-1)*(n-2)%mod*(n-2)%mod)%mod;
55 sum=(sum+2*(n-2)*(m-1)%mod*(m-2)%mod+2*(m-2)*(n-1)%mod*(n-2)%mod)%mod;
56 co<<sum;
57 return 0;
58 }
honoka和格点三角形的更多相关文章
- honoka和格点三角形(牛客寒假训练营day1)
可以把面积为1的好三角形分成两类分开统计:两条边和两个坐标轴平行:只有一条边和某个坐标轴平行. 对于第一种情况,一定是1*2或者2*1的形式,一个1*2的矩形中含有4个不同的三角形.总数是4*((n- ...
- 2020牛客寒假算法基础集训营1 J题可以回顾回顾
2020牛客寒假算法基础集训营1 这套题整体来说还是很简单的. A.honoka和格点三角形 这个题目不是很难,不过要考虑周全,面积是1,那么底边的长度可以是1也可以是2, 注意底边1和2会有重复的, ...
- 【BZOJ2731】三角形覆盖问题
想象一条平行于\(y\)轴的扫描线,从低往高扫描.如何确定关键高度才能使每两个关键高度之间分割出的图形易于计算呢? 关键高度有:三角形底边高度.三角形上顶点高度.三角形交点的高度. 如此分割,我们 ...
- hihocoder #1456 : Rikka with Lattice(杜教筛)
hihocoder #1456 : Rikka with Lattice(杜教筛) 题意 : 给你一个\(n*m\)方格图,统计上面有多少个格点三角形,除了三个顶点,不覆盖其他的格点(包括边和内部). ...
- HZNU ACM一日游 2019.3.17 【2,4,6-三硝基甲苯(TNT)】
Travel Diary 早上8:00到HG,听说hjc20032003在等我. 然后他竟然鸽我...最后还是勉强在8:30坐上去偏僻的HZNU的地铁. 到文新,然后带上fjl,打滴滴,一行人来到了H ...
- Pick定理、欧拉公式和圆的反演
Pick定理.欧拉公式和圆的反演 Tags:高级算法 Pick定理 内容 定点都是整点的多边形,内部整点数为\(innod\),边界整点数\(ednod\),\(S=innod+\frac{ednod ...
- 2016级算法第三次上机-E.ModricWang's Polygons
930 ModricWang's Polygons 思路 首先要想明白,哪些多边形可能是格点正多边形? 分情况考虑: 三角形不可能,因为边长为有理数的正三角形的面积为无理数,而格点三角形的面积为有理数 ...
- luogu 2735 电网 皮克公式
题目链接 题意 给定一个格点三角形,三个顶点分别为(0,0),(n,m),(p,0),求三角形内部的格点个数. 思路 皮克公式: \[S = \frac{i}{2}+b-1\] \(S\)为三角形面积 ...
- 基于GPU的优化处理
http://www.cnblogs.com/wuhanhoutao/archive/2007/11/10/955293.html 早期的三维场景绘制,显卡只是为屏幕上显示像素提供一个缓存,所有的图形 ...
- 牛客小白月赛5 E 面积 计算三角形面积模板 波尔约-格维也纳定理 匹克公式
链接:https://www.nowcoder.com/acm/contest/135/E来源:牛客网 题目描述 定义“最大生成图”:在M*N的点阵中,连接一些点形成一条经过所有点恰好一次的回路,且连 ...
随机推荐
- MetaTown:一个可以自己构建数字资产的平台
摘要:华为云Solution as Code重磅推出<基于MetaTown构建数字资产平台>解决方案. 本文分享自华为云社区<基于MetaTown构建数字资产平台>,作者: 阿 ...
- flutter系列之:flutter中的变形金刚Transform
目录 简介 Transform简介 Transform的使用 总结 简介 虽然我们在开发APP的过程中是以功能为主,但是有时候为了美观或者其他的特殊的需求,需要对组件进行一些变换.在Flutter中这 ...
- EPSS 解读:与 CVSS 相比,孰美?
通用漏洞评分系统(CVSS)是当前应用最频繁的评分系统以评估安全漏洞的严重性.但是,由于该系统在评估漏洞和优先级排序方面存在不足而遭受批评.因此,有部分专业人士呼吁使用漏洞利用预测评分系统(EPSS) ...
- 甜点cc的2022年回顾总结
每每到年底,总会感概时间飞逝,总会莫名的心慌几天. 高中时代我就明白了一个道理:自己决定做的事,就算结果再烂以后也不要后悔,因为那无异于否定过去的自己.人不能总是否定自己的过去,因为我觉得这样会打击自 ...
- 6、发送验证码功能(Redis)
一.业务需求: 1.后端随机生成短信验证码,并在服务器端保存一定时间(redis): 2.将短信验证码发给用户: 3.用户输入短信验证码提交后,在后端与之前生成的短信验证码作比较,如果相同说明验证成功 ...
- CH334、CH335USB2.0Hub芯片(更新ing)
USB HUB又称USB集线器,主要用于USB主机端口扩展,广泛应用于计算机,笔记本,及周边应用.CH334.CH335是符合 USB2.0 协议规范的高性能MTT 4 端口 USB2.0 HUB ...
- (4)go-micro微服务proto开发
目录 一 Protobuf介绍 二 安装Protobuf 三 Protobuf语法 1.1 基本规范 1.2 字段规则 1.3 service如何定义 1.4 Message如何定义 四 proto代 ...
- elasticsearch之exists查询
一.exists查询简介 elastic search提供了exists查询,用以返回字段存在值的记录,默认情况下只有字段的值为null或者[]的时候,elasticsearch才会认为字段不存在: ...
- 2.PyQt5【窗口组件】对话框-Dialog
一.前言 QDialog 类是对话框窗口的基类.对话框窗口是主要用于短期任务以及和用户进行简要 通讯的顶级窗口.QDialog 可以是模态对话框也可以是非模态对话框.QDialog 支持扩展性并 且可 ...
- C Primer Plus (6.16) 編程練習
/*C Primer Plus (6.15) 6*/ 1 #include<stdio.h> 2 int main() 3 { 4 int i,j; 5 for(int i=0;i< ...
