JZOJ 3528. 【NOIP2013模拟11.7A组】图书馆(library)

题目

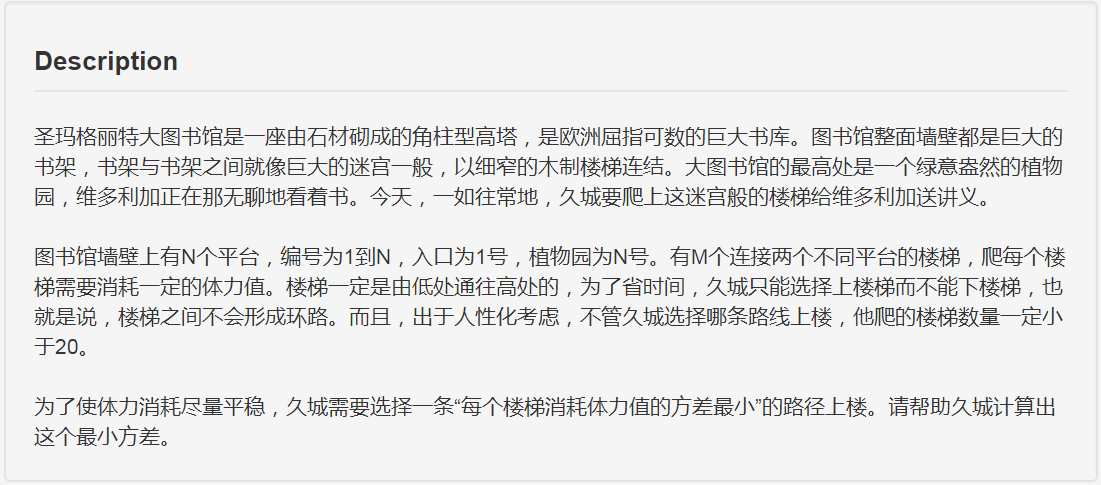
解析

看到这题，没想到 \(dp\)

果断打了暴力

暴力理应只有 \(30\) 左右的样子

然而我加上了些奇技淫巧竟然有 \(80\) 分！

惊到我了！

我 \(80\) 分的暴力：

很容易想到找到所有可找的路计算方差取最小值

然后发现计算方差的所有数中，最大最小差值越小越好

于是果断二分差值，然后枚举最大最小值

再 \(dfs\) 判断并计算答案

于是拿了 \(80\)

\(Code\)

#include<iostream>
#include<cstdio>
using namespace std;

const int N = 55 , M = 305;
int n , m , tot , h[N] , Mx , up , down , pre[N] , edge[N] , flag;
double ans = 1e10;
struct Edge{
	int to , nxt , z;
}e[M];

void dfs(int x , int up , int down)
{
	if (x == n)
	{
		int t = x; double sum = 0 , an = 0 , s = 0;
		while (pre[t]) sum += e[edge[t]].z , t = pre[t] , s++;
		flag = 1 , sum /= s;
		t = x , s = 0;
		while (pre[t]) an += (sum - e[edge[t]].z) * (sum - e[edge[t]].z) , t = pre[t] , s++;
		an /= s;
		if (an < ans) ans = an;
		return;
	}
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		if (e[i].z >= down && e[i].z <= up)
		{
			pre[e[i].to] = x , edge[e[i].to] = i;
			dfs(e[i].to , up , down);
			pre[e[i].to] = edge[e[i].to] = 0;
		}
	}
}

int main()
{
	freopen("library.in" , "r" , stdin);
	freopen("library.out" , "w" , stdout);
	scanf("%d%d" , &n , &m);
	int x , y , z;
	for(register int i = 1; i <= m; i++)
	{
		scanf("%d%d%d" , &x , &y , &z);
		e[++tot] = Edge{y , h[x] , z} , h[x] = tot;
		Mx = max(Mx , z);
	}
	int l = 0 , r = Mx , mid;
	while (l <= r)
	{
		mid = (l + r) >> 1;
		flag = 0;
		for(register int i = 0; i <= Mx - mid; i++)
		{
			down = i , up = i + mid;
			for(register int j = 1; j <= n; j++) pre[j] = edge[j] = 0;
			dfs(1 , up , down);
		}
		if (flag) r = mid - 1;
		else l = mid + 1;
	}
	printf("%.4lf" , ans);
}

正解：其实我们可以先化解求方差的式子

方差就成了 \(\frac{\sum_{i=1}^s {x_i}^2}{n} - ave^2\)

其中 \(ave\) 为平均数，\(s\) 为经过边的个数，\(x_i\) 为边的权值

那么就是说我们最小化方差就只用最小化经过边的权值的平方的和

根据题中走的边数不超过 \(20\)，也就是说 \(s \leq 20\)

我们可以 \(dp\) 了

设 \(f_{i,j,k}\) 表示经过 \(i\) 条边，到了 \(j\) 这个点，走过的路总距离为 \(k\) 时最小的平方和

那么 \(f_{i+1,to,k + l} = min(f_{i,j,k} + l^2)\)

最后答案就是最小的 \(f_{i,n,k}\)

\(Code\)

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;

const int N = 55 , M = 305;
int n , m , tot , h[N] , f[25][55][1005];
double ans = 1e10;
struct Edge{
	int to , nxt , z;
}e[M];

int main()
{
	freopen("library.in" , "r" , stdin);
	freopen("library.out" , "w" , stdout);
	scanf("%d%d" , &n , &m);
	int x , y , z;
	for(register int i = 1; i <= m; i++)
	{
		scanf("%d%d%d" , &x , &y , &z);
		e[++tot] = Edge{y , h[x] , z} , h[x] = tot;
	}
	memset(f , 0x3f3f3f , sizeof f);
	f[0][1][0] = 0;
	for(register int i = 0; i <= 20; i++)
		for(register int j = 1; j <= n; j++)
			for(register int l = 0; l <= 1000; l++)
			for(register int k = h[j]; k; k = e[k].nxt)
			if (l + e[k].z <= 1000) f[i + 1][e[k].to][l + e[k].z] = min(f[i + 1][e[k].to][l + e[k].z] , f[i][j][l] + e[k].z * e[k].z);
	for(register int i = 1; i <= 20; i++)
		for(register int j = 0; j <= 1000; j++)
			ans = min(ans , (double)f[i][n][j] / (1.0 * i) - (1.0 * j / i) * (1.0 * j / i));
	printf("%.4lf" , abs(ans));
}