2020-09-13：判断一个正整数是a的b次方，a和b是整数，并且大于等于2，如何求解？

福哥答案2020-09-13：

首先确定b的范围，b的范围一定在[2,logN]里。然后遍历b，求a的范围，如果范围长度等于0，说明这个正整数是a的b次方。
1.遍历b范围。二分法求a，a初始范围是[2,logN]。2的400次方耗时5秒。【有代码】
2.遍历b范围。优化二分法求a，a初始范围是[2,上一次a的结果]。2的10000次方耗时5秒。【有代码】
3.应该有更优化的方案，暂时没想到。【无代码】

因为用到了大整数，所以用python语言编写。代码如下：

#!/usr/bin/python3
import time
from functools import wraps
def _get_sqrt_range(num, right, exp=2):
    """
        求num的exp开方,exp是指数，num是结果。求底数。
        Args:
            num: 大于等于0并且是整数。
            right: 大于等于0并且是整数。右边界。
            exp: 大于等于0并且是整数。
        Returns:
            返回元组，表示一个开方范围。
        Raises:
            IOError: 无错误。
    """
    left = 1
    if num == 0:
        return 0, 0
    if num == 1:
        return 1, 1
    if num == 2 or num == 3:
        return 1, 2
    while True:
        mid = (left + right) // 2
        if mid ** exp > num:
            right = mid
            if left ** exp == num:
                return left, left
            if left + 1 == right:
                return left, right
        elif mid ** exp < num:
            left = mid
            if right ** exp == num:
                return right, right
            if left + 1 == right:
                return left, right
            if mid == 1:
                return 1, 2
        else:
            return mid, mid

def get_log_range(num, basenum):
    """
        求对数范围。
        Args:
            num: 数，大于等于1并且是整数。
            basenum: 底数，大于等于2并且是整数。
        Returns:
            返回结果。对数范围。
        Raises:
            IOError: 无错误。
    """
    if num == 1:
        return 0, 0
    else:
        n = 0
        ism = 0
        while num >= basenum:
            if ism == 0 and num % basenum != 0:
                ism = 1
            n += 1
            num //= basenum
        return n, n + ism

def timefn(fn):
    """计算性能的修饰器"""
    @wraps(fn)
    def measure_time(*args, **kwargs):
        t1 = time.time()
        result = fn(*args, **kwargs)
        t2 = time.time()
        print(f"@timefn: {fn.__name__} took {t2 - t1: .5f} s")
        return result
    return measure_time

@timefn
def is_power1(num):
    """
        判断n是否是一个数的幂次方形式。
        Args:
            num: 大于等于0并且是整数。
        Returns:
            返回结果。true是幂数
        Raises:
            IOError: 无错误。
    """
    if num <= 3:
        return False
    else:
        log_range = get_log_range(num, 2)
        if log_range[0] == log_range[1]:
            return True
        expmax = log_range[0]
        expmin = 2
        exp = expmin
        sqrt = 0
        right = 2 ** (1 + log_range[0] // 2)
        while exp <= expmax:
            sqrt = _get_sqrt_range(num, right, exp)
            # right = sqrt[0]#缩小右边界范围
            if sqrt[0] == sqrt[1]:
                return True
            if sqrt == (1, 2):
                return False
            exp += 1
        return False

@timefn
def is_power2(num):
    """
        判断n是否是一个数的幂次方形式。
        Args:
            num: 大于等于0并且是整数。
        Returns:
            返回结果。true是幂数
        Raises:
            IOError: 无错误。
    """
    if num <= 3:
        return False
    else:
        log_range = get_log_range(num, 2)
        if log_range[0] == log_range[1]:
            return True
        expmax = log_range[0]
        expmin = 2
        exp = expmin
        sqrt = 0
        right = 2 ** (1 + log_range[0] // 2)
        while exp <= expmax:
            sqrt = _get_sqrt_range(num, right, exp)
            right = sqrt[0]  # 缩小右边界范围
            if sqrt[0] == sqrt[1]:
                return True
            if sqrt == (1, 2):
                return False
            exp += 1
        return False

if __name__ == "__main__":
    print("----2的400次方")
    num = 2 ** 400 + 1
    print(is_power1(num))
    print(is_power2(num))
    print("\r\n----2的10000次方")
    num = 2 ** 10000 + 1
    print(is_power2(num))

　　

执行代码结果如下：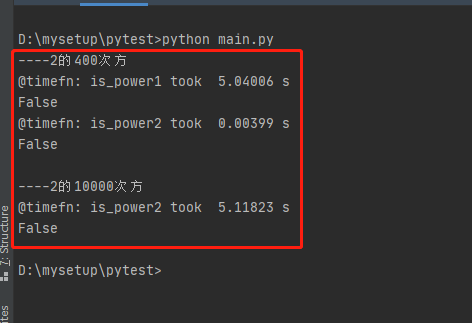

***
[评论](https://user.qzone.qq.com/3182319461/blog/1599951713)