2023-01-02：某天，小美在玩一款游戏，游戏开始时，有n台机器， 每台机器都有一个能量水平，分别为a1、a2、…、an， 小美每次操作可以选其中的一台机器，假设选的是第i台， 那小美可以将其变成

2023-01-02：某天，小美在玩一款游戏，游戏开始时，有n台机器，
每台机器都有一个能量水平，分别为a1、a2、…、an，
小美每次操作可以选其中的一台机器，假设选的是第i台，
那小美可以将其变成 ai+10^k（k为正整数且0<=k<=9），
由于能量过高会有安全隐患，所以机器会在小美每次操作后会自动释放过高的能量
即变成 (ai+10^k)%m
其中%m表示对m取模，由于小美还有工作没有完成，所以她想请你帮她计算一下，
对于每台机器，将其调节至能量水平为0至少需要多少次操作
（机器自动释放能量不计入小美的操作次数）。
第一行两个正整数n和m，表示数字个数和取模数值。
第二行为n个正整数a1, a2,… an，其中ai表示第i台机器初始的能量水平。
1 <= n <= 30000，2 <= m <= 30000, 0 <= ai <= 10^12。
来自美团。

答案2023-01-02：

打表法。
用rust和solidity写代码。

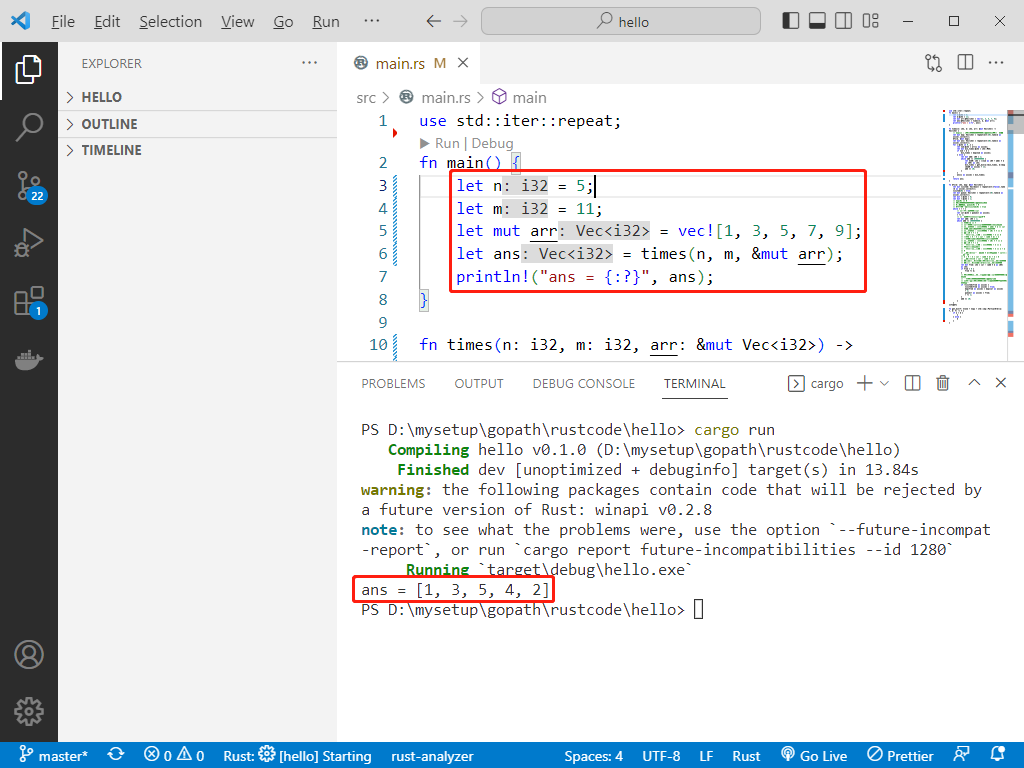
代码用rust编写。代码如下：

use std::iter::repeat;
fn main() {
    let n = 5;
    let m = 11;
    let mut arr = vec![1, 3, 5, 7, 9];
    let ans = times(n, m, &mut arr);
    println!("ans = {:?}", ans);
}

fn times(n: i32, m: i32, arr: &mut Vec<i32>) -> Vec<i32> {
    // map[i] : i这个余数变成余数0，需要至少操作几次？
    let mut map: Vec<i32> = repeat(0).take(m as usize).collect();
    bfs(m, &mut map);
    let mut ans: Vec<i32> = repeat(0).take(n as usize).collect();
    for i in 0..n {
        let num = arr[i as usize];
        let mut min_times = i32::MAX;
        if num < m {
            min_times = map[num as usize];
        } else {
            let mut add: i64 = 1;
            while add <= 1000000000 {
                let mod0: i32 = ((num as i64 + add) % m as i64) as i32;
                min_times = get_min(min_times, map[mod0 as usize] + 1);
                add *= 10;
            }
        }
        ans[i as usize] = min_times;
    }
    return ans;
}

fn bfs(m: i32, map: &mut Vec<i32>) {
    let mut visited: Vec<bool> = repeat(false).take(m as usize).collect();
    visited[0] = true;
    let mut queue: Vec<i32> = repeat(0).take(m as usize).collect();
    let mut l = 0;
    let mut r = 1;
    // map[0] == 0
    // 表示余数0变成余数0，需要至少0次
    // 0进队列了, queue[0] = 0
    // 0算访问过了，visited[0] = true
    while l < r {
        // 当前弹出的余数是cur
        let cur = queue[l as usize];
        l += 1;
        // 能加的数字，从1枚举到10^9
        let mut add: i64 = 1;
        while add <= 1000000000 {
            // 比如，m == 7
            // 当前余数是cur，cur变成余数0，至少要a次
            // 我们想知道 : (哪个余数b + add) % m == cur
            // 比如,add=10的时候，cur==5的时候
            // 我们想知道 : (哪个余数b + 10) % 7 == 5
            // 因为10 % 7 = 3
            // 所以其实我们在求 : 哪个余数b + 3 == 5
            // 显然b = 5 - 3 = cur - (add % m) = 2
            // 再比如，add=10的时候，cur==2的时候
            // 我们想知道 : (哪个余数b + 10) % 7 == 2
            // 因为10 % 7 = 3
            // 所以其实我们在求 : 哪个余数b + 3 == 2
            // 这明显是不对的，
            // 所以其实我们在求 : 哪个余数b + 3 == 2 + m == 9
            // 也就是b，通过加了add % m，来到了m + cur，多转了一圈
            // b = 9 - 3 = cur - (add % m) + m = 6
            // 也就是说，b = cur - (add % m)，
            // 如果不小于0，那就是这个b，是我们要找的余数
            // 如果小于0，那就是b+m，是我们要找的余数
            let mut from: i32 = cur - (add % m as i64) as i32;
            if from < 0 {
                from += m;
            }
            // 这个余数我们终于找到了，因为cur变成余数0，需要a次
            // 所以这个余数变成余数0，需要a+1次
            // 当然前提是这个余数，之前宽度优先遍历的时候，没遇到过
            if !visited[from as usize] {
                visited[from as usize] = true;
                map[from as usize] = map[cur as usize] + 1;
                queue[r as usize] = from;
                r += 1;
            }
            add *= 10;
        }
    }
}

fn get_min<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
    if a < b {
        a
    } else {
        b
    }
}

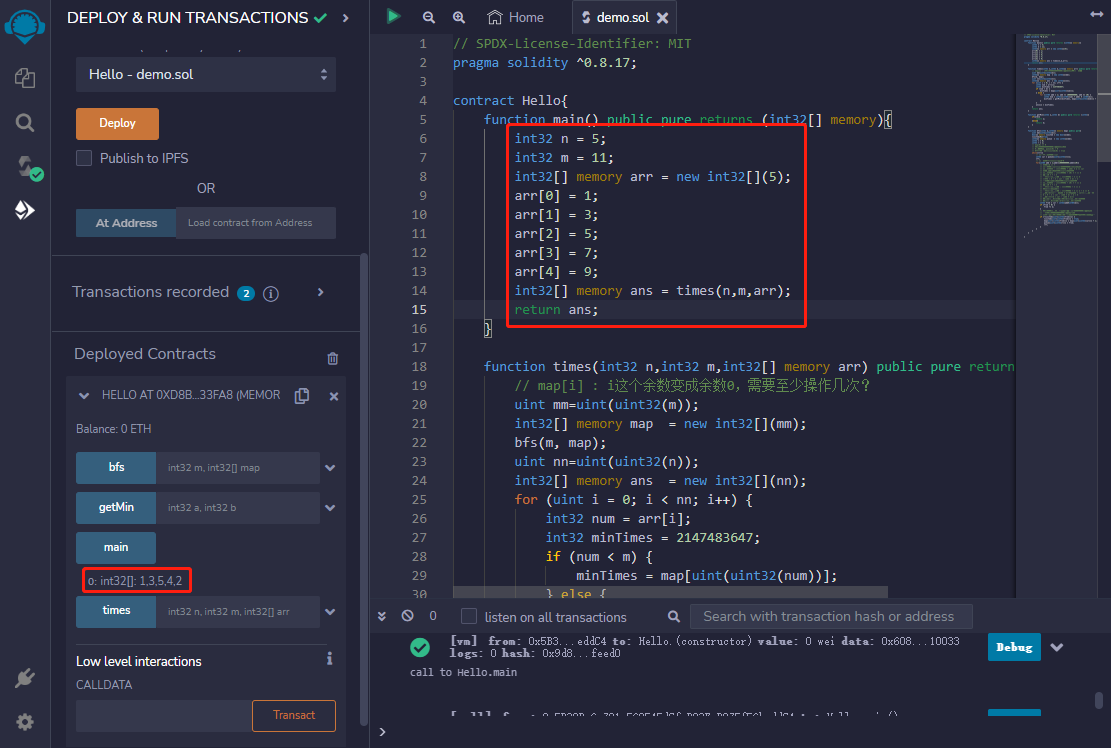
代码用solidity编写。代码如下：

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.17;

contract Hello{
    function main() public pure returns (int32[] memory){
        int32 n = 5;
        int32 m = 11;
        int32[] memory arr = new int32[](5);
        arr[0] = 1;
        arr[1] = 3;
        arr[2] = 5;
        arr[3] = 7;
        arr[4] = 9;
        int32[] memory ans = times(n,m,arr);
        return ans;
    }

    function times(int32 n,int32 m,int32[] memory arr) public pure returns (int32[] memory){
		// map[i] : i这个余数变成余数0，需要至少操作几次？
        uint mm=uint(uint32(m));
        int32[] memory map  = new int32[](mm);
		bfs(m, map);
        uint nn=uint(uint32(n));
        int32[] memory ans  = new int32[](nn);
		for (uint i = 0; i < nn; i++) {
			int32 num = arr[i];
			int32 minTimes = 2147483647;
			if (num < m) {
				minTimes = map[uint(uint32(num))];
			} else {
				for (int64 add = 1; add <= 1000000000; add *= 10) {
					int32 mod = int32((int64(num) + add) % int64(m));
					minTimes = getMin(minTimes, map[uint(uint32(mod))] + 1);
				}
			}
			ans[i] = minTimes;
		}
		return ans;
    }

    function getMin(int32 a,int32 b) public pure returns (int32){
        if(a<b){
            return a;
        }else{
            return b;
        }
    }

    function bfs(int32 m,int32[] memory map) public pure{
        uint mm=uint(uint32(m));
        bool[] memory visited = new bool[](mm);
        visited[0]=true;
        int32[] memory queue  = new int32[](mm);
        int32 l = 0;
        int32 r = 1;
        // map[0] == 0
		// 表示余数0变成余数0，需要至少0次
		// 0进队列了, queue[0] = 0
		// 0算访问过了，visited[0] = true
        while(l<r){
			// 当前弹出的余数是cur
            int32 cur = queue[uint(uint32(l))];
            l++;
			// 能加的数字，从1枚举到10^9
            for(int64 add = 1;add<=1000000000;add*=10){
				// 比如，m == 7
				// 当前余数是cur，cur变成余数0，至少要a次
				// 我们想知道 : (哪个余数b + add) % m == cur
				// 比如,add=10的时候，cur==5的时候
				// 我们想知道 : (哪个余数b + 10) % 7 == 5
				// 因为10 % 7 = 3
				// 所以其实我们在求 : 哪个余数b + 3 == 5
				// 显然b = 5 - 3 = cur - (add % m) = 2
				// 再比如，add=10的时候，cur==2的时候
				// 我们想知道 : (哪个余数b + 10) % 7 == 2
				// 因为10 % 7 = 3
				// 所以其实我们在求 : 哪个余数b + 3 == 2
				// 这明显是不对的，
				// 所以其实我们在求 : 哪个余数b + 3 == 2 + m == 9
				// 也就是b，通过加了add % m，来到了m + cur，多转了一圈
				// b = 9 - 3 = cur - (add % m) + m = 6
				// 也就是说，b = cur - (add % m)，
				// 如果不小于0，那就是这个b，是我们要找的余数
				// 如果小于0，那就是b+m，是我们要找的余数
                int32 from = cur - int32(add%int64(m));
				if (from < 0) {
					from += m;
				}
				// 这个余数我们终于找到了，因为cur变成余数0，需要a次
				// 所以这个余数变成余数0，需要a+1次
				// 当然前提是这个余数，之前宽度优先遍历的时候，没遇到过
				if (!visited[uint(uint32(from))]) {
					visited[uint(uint32(from))] = true;
					map[uint(uint32(from))] = map[uint(uint32(cur))] + 1;
					queue[uint(uint32(r))] = from;
                    r++;
				}
            }
        }
    }

}