Weights Assignment For Tree Edges

题目：

（我的题目很长，你忍一下……）

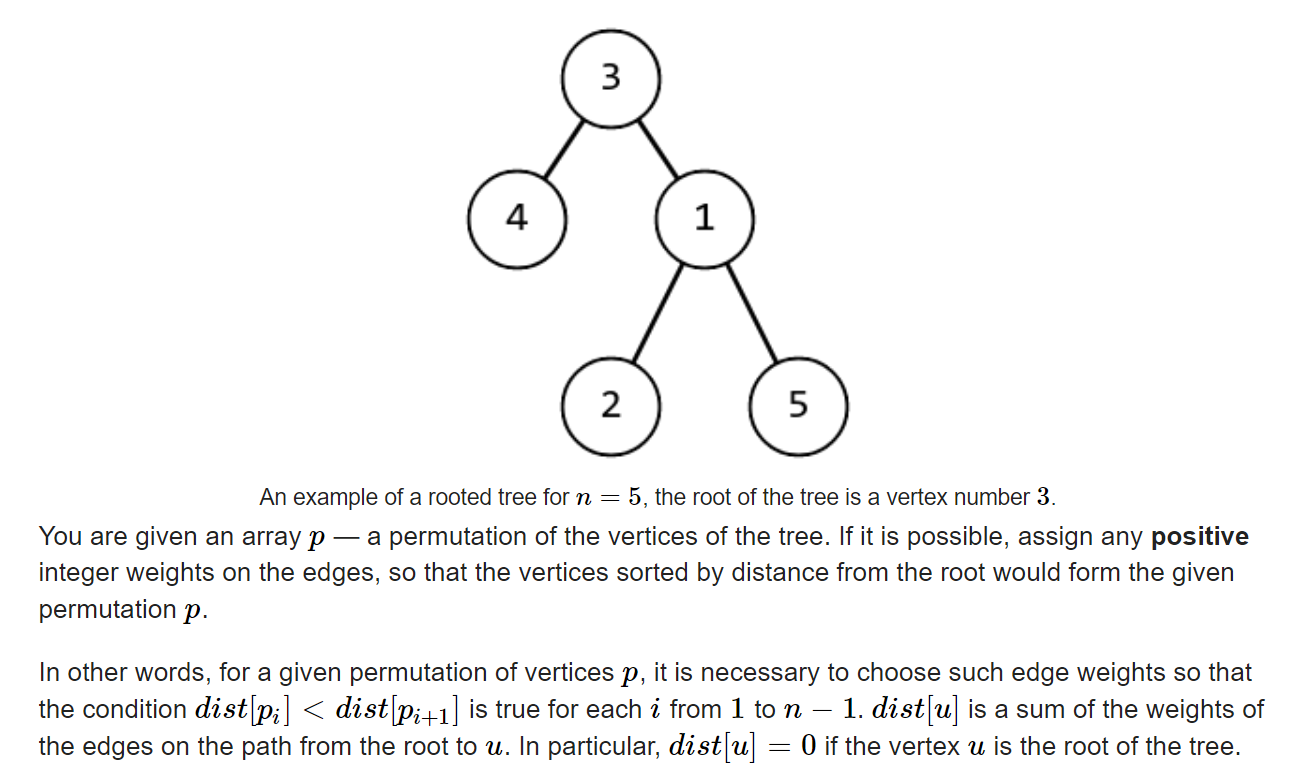
题目分析：

这道题目的体面比较复杂，先是讲了一下树是怎样的一个结构，并且告诉我们在这里，他是以什么样的一种方式描述一棵树的，就是通过描述每个节点的父节点是哪个（b数组），然后告诉我们要安排边权，使得树中的每个节点到根的距离都能如同p数组那样进行排序，然后叫我们输出对应每个点和他的父结点之间的边权即可。

题解：

首先这道题是一道非常经典的让我们判断能否构造一个数组，使得题干条件成立，如果不能输出-1；

既然这样的话，我们肯定要先分析什么情况下会输出-1，那么就是一个节点到根的距离反而比它父节点到根的距离更近，我们知道这是不可能的，因为在这里所有的边权都只可能是正数，所以我们就要去看是否存在这种情况，但是根据b数组我们只能知道这个节点的父结点是什么，并不能很快的查找到这个点的所有子节点，所以我们这里就要运用我们在Acwing上学到的邻接表来存储，这样就可以很快遍历当前节点的所有子节点，这一步是在输入b数组的时候同步进行的。但是光找到子节点没有用，我们不能用O（1）的时间复杂度直接找到这个子节点的位置，所以我们要对p数组进行修改，使得P[i]代表的是i是离根最近的第P[i]个点，这样就能根据P数组直接得到每个点的位置；

只要能经过上一步的检查，那么到这里的就一定能构造出一个对应的距离，我们这样考虑，每个到根的距离的差只差1，比如0，1，2，3……n。 所以我们定义一个maxd表示当前到根的最大的距离，然后下一个点到根的距离就是maxd，那么这个点到父结点的边权就是maxd + 1 - dist[father]，所以我们还要定义一个dist数组存储当前节点到根的距离，但是这样的话，我们遍历的顺序就应该是从近到远，所以那个P数组我们要换个形式使之保留。 这里整个的思路就是设定每个点到根节点的距离，然后进行赋值。

从题目中，我们可以看出，这是一道非常经典的用空间换时间的思路，我开了很多的数组，就是为了在为了找到它时能用O（1）的效率找到；

代码：Submission #153732004 - Codeforces