「SOL」序列计数sequence (模拟赛)

看了题解过后觉得好像有点熟悉……但是总之是想不起来怎么做的了，自己的做法也和题解不一样。

是一道很好的题啦，把两种做法都写一下作个总结。

题面

给定一个长度为 \(n\) （\(n\le 10^5\)）的字符串 \(S\)，字符集 \(\Sigma\) 仅包含前 \(10\) 种英文小写字母。再给定 \(Q\) 次（\(Q\le 10^6\)）询问，每次给出区间 \([L, R]\)，输出 \(S\) 的子段 \(S[L, R]\) 中有多少个本质不同的子序列，不含空串。

答案对 \(10^9+7\) 取模。

解析

解法1：序列自动机+猫树分治

最近对猫树分治比较上瘾，看啥区间询问都像猫树分治……

如果你觉得这是个自己没有见过的算法，说不定只是你没见过它的名字……就是把区间从中间划开，每次处理跨过区间中点的询问的算法。

首先考虑暴力怎么做。看到“本质不同的子序列”，就想到了序列自动机；就像看到“本质不同的子串”就想到后缀自动机一样。于是我们可以暴力建出子串的序列自动机，再拓扑做一遍 DP 即可。本质上是在求序列自动机这个 DAG 上的非空路径条数。

序列自动机是非常特殊的 DAG，拓扑序就是从左到右。记位置 \(i\) 之前的第一个 \(S_i\) 的位置在 \(las_i\)，那么拓扑 DP 的式子就可以写为：

\[dp_i=\sum_{j=las_i}^{i-1}dp_j+1
\]

然后考虑优化，注意到字符集大小只有 \(10\)，说不定维护两个区间的某些信息后可以快速合并计算答案。于是可以想到猫树分治，那么需要解决的问题就是：询问 \([l,r]\) 跨过了分治中点 \(m\)，维护 \([l,m]\) 的信息和 \([m+1,r]\) 的信息，支持快速合并计算答案。

先分析区间合并需要哪些信息：

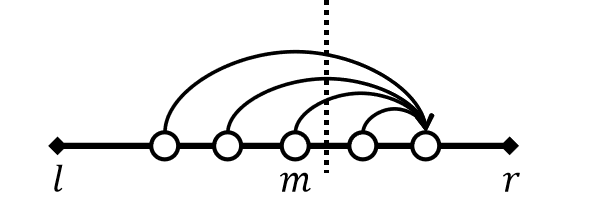
左区间的 DP 值是确定的（不需要用到左区间之外的信息），但是右区间转移时可能会用到左区间的一些 DP 值，更确切地说，是左区间的一些后缀的 DP 值之和。记 \(p_c\) 为字符 \(c\) 在左区间最后一次出现的位置，若未出现则默认为左区间开头。记 \(Sdp_c\)：

\[Sdp_c=\sum_{i=p_c}^m
\]

不难发现右区间的 DP 值可以完全用 \(Sdp_{c}\)（\(0\le c\le 9\)）的一次多项式来表示，于是我们可以预处理右区间的DP 前缀和用 \(Sdp\) 表示的结果。

\[\sum_{i=m+1}^{r}dp_i=\sum_{c\in \Sigma}Sdp_{l,c}\times a_{r,c}
\]

于是左区间需要预处理的就是：

后缀的 DP 值之和；
后缀的 \(Sdp_c\) 的确切值。

之前提到这个 DP 本质上是在求 DAG 上的路径条数，那么求 \(Sdp_c\) 其实就是在求以 \([p_c,m]\) 结尾的路径的条数。

注意到 DP 不一定要顺着拓扑序，也可以倒着做——求从一个点出发的路径。由于左区间的预处理是每次向左扩展一个点，这样定义 DP 会更容易。具体地，定义

\(f_i\)：左区间内从 \(i\) 出发的路径条数；
\(g_{i,c}\)：左区间内从 \(i\) 出发，在 \([p_c,m]\) 结束的路径条数。

序列自动机还有一个特点：一个点的入度可以很大，但是出度是字符集大小 \(|\Sigma|\)。所以我们可以 \(\mathcal O(|\Sigma|)\) 计算出单个 \(f_i,g_{i,c}\)。这意味着预处理左区间要 \(\mathcal O(n|\Sigma|^2)\)？好像不够快的样子……再观察，注意到相邻两个点能够转移到的点集只有一个点不同，于是可以 \(\mathcal O(|\Sigma|)\) 在上一个点的 DP 值上修改。

最后预处理左右区间的复杂度都是 \(\mathcal {O(n|\Sigma|)}\)，询问可以 \(\mathcal O(|\Sigma|)\) 合并左右区间，最终复杂度 \(\mathcal O\Big((Q + n\log n)|\Sigma|\Big)\)，足以通过本题。

解法2：矩阵求逆

换一种 DP 的定义，不从序列自动机考虑：\(dp_{i,c}\) 表示已经决策到第 \(i\) 个字符，当前子序列以 \(c\) 结尾的方案数。这种定义天然保证了本质不同。

以下用 \(R\) 代称 \(|\Sigma|\)。

转移只需要决策当前字符选不选，如果选，则上一个字符是什么。由于 \(|\Sigma|\) 很小，可以直接写出矩阵的形式。显然转移矩阵只与 \(i\) 处的字符 \(c\) 有关（第 \(R\) 行用来表示空串）。

\[D_i=\begin{bmatrix}dp_{i,0}\\dp_{i,1}\\\vdots\\dp_{i,R}\end{bmatrix},V_{c,i,j}=\begin{cases}1&(i=j)\\1&(i=c)\\0&otherwise\end{cases}
\]

转移即为

\[D_i=V_{S_i}D_{i-1}
\]

所以答案就是一个区间的矩阵之积。套路地，我们发现我们并不需要整个矩阵，而是一个位置的值。具体地，我们需要的是：

\[\begin{pmatrix}1&1&\cdots&1\end{pmatrix}\times V_{S_l}\times V_{S_{l+1}}\times\cdots\times V_{S_r}\times\begin{pmatrix}0\\0\\\vdots\\1\end{pmatrix}
\]

由于矩阵长得特殊，我们可以手推矩阵的逆（虽然看题解之前我也忘了该怎么手推）。于是可以转换成矩阵的前缀积以及矩阵的逆的前缀积的形式：

\[\begin{aligned}
&M_i=V_{S_1}\times V_{S_2}\times\cdots\times V_{S_i}\\
&N_i=V_{S_i}^{-1}\times V_{S_{i-1}}^{-1}\times\cdots\times V_{S_1}^{-1}\\
&A=\begin{pmatrix}1&1&\cdots&1\end{pmatrix},B=\begin{pmatrix}0\\0\\\vdots\\1\end{pmatrix}\\
&ans=A\times N_{l-1}\times M_r\times B
\end{aligned}
\]

于是可以预处理行列向量：

\[\begin{aligned}
&I_i=A\times N_{i},J_i=M_i\times B
\end{aligned}
\]

具体预处理的方法以 \(J_i\) 为例，\(I_i\) 类似。

首先会发现 \(J_i=M_{i-1}\times V_{S_i}\times B\)，这导致我们没法直接用 \(J_{i-1}\) 乘上一个矩阵得到 \(J_i\)。于是不可避免地要矩阵乘法。但是一定要用 \(\mathcal O(R^3)\) 的矩阵乘法吗？注意到 \(V_{S_i}\) 非常特殊——

\[M_{i,p,q}=\begin{cases}M_{i-1,p,q}&q=S_i\\M_{i-1,p,q}+M_{i-1,p,S_i}&q\neq S_i\end{cases}
\]

除了第 \(S_i\) 列，其他位置都加上了相同行的第 \(S_i\) 列的值。我们可以打一个“全局加 \(S_i\) 列”的 tag，但是 \(S_i\) 列本身并没有加，那我们就反过来，打上全局加 tag 后把这一列减去第 \(S_i\) 列，即清零。

这样就可以快速维护矩阵。对于 \(J_i\)，实际上 \(J_{i,p}=M_{i,p,R}\)，只需要矩阵最后一列的确切值；对于 \(I_i\)，\(I_{i,p}=\sum_q N_{i,q,p}\)，还需要同时维护矩形每一列的和。

最后复杂度可以做到 \(\mathcal O(n|\Sigma|^2+Q|\Sigma|)\)

源代码

点击展开/折叠源代码(猫树分治)

/* Lucky_Glass */

#include <queue>

#include <cstdio>

#include <cstring>

#include <algorithm>

const int N = 5e5 + 10, MOD = 1e9 + 7;

inline int add(int a, const int &b) { return (a += b) >= MOD ? a - MOD : a; }

inline int sub(int a, const int &b) { return (a -= b) < 0 ? a + MOD : a; }

inline int mul(const int &a, const int &b) { return int(1ll * a * b % MOD); }

#define ITERON(a, b, fun) a = fun(a, b)

char str[N];

int las_pos[N], qry[N][2], ans[N];

int n;

int doBF(const int &le, const int &ri) {

  static int bf_sumf[N];

  bf_sumf[le - 1] = 0;

  for (int i = le; i <= ri; ++i) {

    int fi;

    if (las_pos[i] < le) fi = add(1, bf_sumf[i - 1]);

    else fi = sub(bf_sumf[i - 1], bf_sumf[las_pos[i] - 1]);

    bf_sumf[i] = add(bf_sumf[i - 1], fi);

  }

  return bf_sumf[ri];

}

const int BOND = 200;

int qry_id[N], tmp_qry_id[N];

int f[N][11], sum_f[N][11];

void solveDac(const int &le, const int &ri, const int &ql, const int &qr) {

  if (ql > qr) return;

  if (le + BOND >= ri) return;

  int las_ind[13] = {}, tmp_sum[13] = {};

  int mi = (le + ri) >> 1;

  for (int i = mi; i >= le; --i) {

    for (int c = 0; c <= 10; ++c)

      f[i][c] = add(tmp_sum[c], !las_ind[c]);

    if (las_ind[str[i] - 'a'])

      for (int c = 0; c <= 10; ++c)

        ITERON(tmp_sum[c], f[las_ind[str[i] - 'a']][c], sub);

    las_ind[str[i] - 'a'] = i;

    for (int c = 0; c <= 10; ++c)

      ITERON(tmp_sum[c], f[i][c], add);

    for (int c = 0; c <= 10; ++c)

      sum_f[i][c] = add(tmp_sum[c], !las_ind[c] && c < 10);

  }

  for (int i = mi + 1; i <= ri; ++i)

    for (int c = 0; c < 10; ++c) {

      if (las_pos[i] - 1 <= mi) {

        if (i == mi + 1) f[i][c] = 0;

        else f[i][c] = sum_f[i - 1][c];

      } else {

        f[i][c] = sub(sum_f[i - 1][c], sum_f[las_pos[i] - 1][c]);

      }

      if (las_pos[i] <= mi && str[i] - 'a' == c) ITERON(f[i][c], 1, add);

      if (i == mi + 1) sum_f[i][c] = f[i][c];

      else sum_f[i][c] = add(sum_f[i - 1][c], f[i][c]);

    }

  int nql = ql - 1, nqr = qr + 1;

  for (int i = ql; i <= qr; ++i)

    if (qry[qry_id[i]][1] < mi) {

      tmp_qry_id[++nql] = qry_id[i];

    } else if (qry[qry_id[i]][0] > mi) {

      tmp_qry_id[--nqr] = qry_id[i];

    } else {

      int qle = qry[qry_id[i]][0], qri = qry[qry_id[i]][1];

      int &res = ans[qry_id[i]] = sum_f[qle][10];

      if (qri == mi) continue;

      for (int c = 0; c < 10; ++c)

        ITERON(res, mul(sum_f[qle][c], sum_f[qri][c]), add);

    }

  for (int i = ql; i <= nql; ++i) qry_id[i] = tmp_qry_id[i];

  for (int i = nqr; i <= qr; ++i) qry_id[i] = tmp_qry_id[i];

  solveDac(le, mi, ql, nql);

  solveDac(mi + 1, ri, nqr, qr);

}

int rin(int &r) {

  int c = getchar(); r = 0;

  while (c < '0' || '9' < c) c = getchar();

  while ('0' <= c && c <= '9') r = r * 10 + (c ^ '0'), c = getchar();

  return r;

}

int main() {

  scanf("%s", str + 1);

  n = (int)strlen(str + 1);

  int tmp_las_pos[20] = {};

  for (int i = 1; i <= n; ++i) {

    las_pos[i] = tmp_las_pos[str[i] - 'a'];

    tmp_las_pos[str[i] - 'a'] = i;

  }

  int qry_cnt = 0, ncas = rin(ncas);

  for (int i = 1; i <= ncas; ++i) {

    rin(qry[i][0]), rin(qry[i][1]);

    if (qry[i][0] + BOND >= qry[i][1]) ans[i] = doBF(qry[i][0], qry[i][1]);

    else qry_id[++qry_cnt] = i;

  }

  solveDac(1, n, 1, qry_cnt);

  for (int i = 1; i <= ncas; ++i)

    printf("%d\n", ans[i]);

  return 0;

}

点击展开/折叠源代码(矩阵求逆)

/*Lucky_Glass*/

#include <cstdio>

#include <cstring>

#include <algorithm>

const int N = 5e5 + 10, MOD = 1e9 + 7;

#define con(typ) const typ &

inline int add(int a, con(int) b) {return (a += b) >= MOD ? a - MOD : a;}

inline int sub(int a, con(int) b) {return (a -= b) < 0 ? a + MOD : a;}

inline int mul(con(int) a, con(int) b) {return int(1ll * a * b % MOD);}

inline int rin(int &r) {

  int c = getchar(); r = 0;

  while ( c < '0' || '9' < c ) c = getchar();

  while ( '0' <= c && c <= '9' ) r = (r * 10) + (c ^ '0'), c = getchar();

  return r;

}

int n, totad, m;

char str[N];

int ad[11], neg[N][11], psi[N][11], cur2[11][11], cur[11][11], totcur[11];

int main() {

  scanf("%s", str + 1);

  n = int(strlen(str + 1));

  for (int i = 0; i <   11; ++i) {

    for (int j = 0; j < 11; ++j)

      cur2[i][j] = cur[i][j] = i == j;

    totcur[i] = 1;

  }

  for (int i = 1; i <= n; ++i) {

    int c = str[i] - 'a';

    for (int j = 0; j < 11; ++j) {

      int tmp2 = ad[j];

      ad[j] = add(ad[j], add(cur[c][j], ad[j]));

      cur[c][j] = sub(0, tmp2);

      totcur[j] = sub(totcur[j], cur2[j][c]);

      cur2[j][c] = sub(cur2[j][c], totcur[j]);

      totcur[j] = add(totcur[j], cur2[j][c]);

    }

    for (int j = 0; j < 11; ++j) {

      psi[i][j] = add(cur[10][j], ad[j]);

      neg[i][j] = sub(totcur[j], cur2[j][10]);

    }

  }

  for (int j = 0; j < 10; ++j)

    neg[0][j] = 1;

  rin(m);

  while ( m-- ) {

    int le, ri; rin(le), rin(ri);

    --le;

    int ans = 0;

    for (int i = 0; i < 11; ++i)

      ans = add(ans, mul(psi[ri][i], neg[le][i]));

    printf("%d\n", ans);

  }

  return 0;

}

THE END

Thanks for reading!

告别土壤，白桦再难生长。
植根星海，又能否重获青苍？
每夜放逐信仰，四光年之外去流浪——
纵躯壳埋葬，灵魂自由释放。

——《岁月成碑》By 乐正绫 / Days

> Link 岁月成碑 - 网易云