迁移学习（MEnsA）《MEnsA: Mix-up Ensemble Average for Unsupervised Multi Target Domain Adaptation on 3D Point Clouds》

论文信息

论文标题：MEnsA: Mix-up Ensemble Average for Unsupervised Multi Target Domain Adaptation on 3D Point Clouds
论文作者：Ashish Sinha, Jonghyun Choi
论文来源：2023 CVPR
论文地址：download 
论文代码：download
视屏讲解：click

1 前言

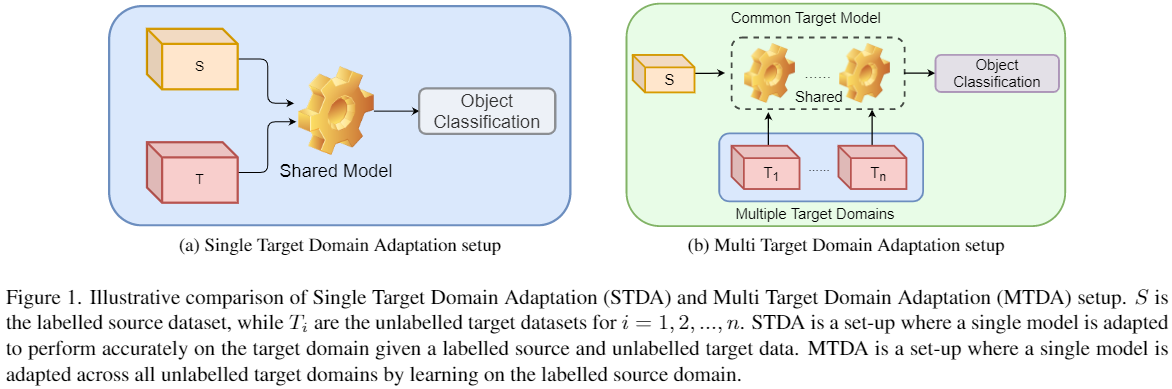
　　单目标域和多目标域

2 介绍

　　单目标域和多目标域的差异：

　　

3 方法

3.1 整体框架

　　

3.2 域 mixup 模块

　　Mixup 模块：

　　　　$F_{i}^{m}=\lambda F_{s}+(1-\lambda) F_{T_{i}}  \quad\quad(1)$

　　　　$L_{i}^{m}=\lambda L_{s}+(1-\lambda) L_{T_{i}}   \quad\quad(2)$

　　线性差值的好处：

• • 有助于创建一个连续域不变的潜在空间，使混合特征能够映射到源域和目标域的潜在空间之间的位置，这种连续的潜在空间对于跨多个域的域不变推理至关重要；
  • 作为一个有效的正则化器，帮助领域分类器 $D$ 在预测混合特征嵌入 $F_{mi}$ 的领域(源或目标) 的软分数方面有所提高；

3.3 对比

　　

　　基线：【多目标域场景下】

• • 形式：单源域和单目标域线性差值；
  • 问题：存在灾难性遗忘问题，只专注于学习源域和一个目标域之间的域不变特征，忽略了跨多个域的共享特征；

　　本文：单源域 和 多目标域集成线性差值；

• • 形式：$F_{m}^{M}=\frac{1}{n} \sum_{i=1}^{n} F_{i}^{m}  \quad\quad(3)$；
  • 目的：旨在捕获跨多个域共享的域不变特征，减轻域间的冲突信息，提高泛化性；

3.4 训练目标

　　总损失：

　　　　$\mathcal{L}=\log \left(\sum\left(e^{\gamma\left(\mathcal{L}_{c l s}+\eta \mathcal{L}_{d c}+\zeta \mathcal{L}_{a d v}\right)}\right)\right) / \gamma  \quad\quad(4)$

　　其中：

　　　　源域分类损失： $\mathcal{L}_{c l s}  =\mathcal{L}_{C E}\left(C\left(F_{s}\right), y_{s}\right)  \quad\quad(4)$

　　　　单源域单目标域鉴别损失：$\mathcal{L}_{d c}  =\mathcal{L}_{C E}\left(D\left(F_{s}\right), L_{s}\right)+\mathcal{L}_{C E}\left(D\left(F_{T_{i}}, L_{T_{i}}\right)\right)    \quad\quad(5)$

　　　　对抗损失：$\mathcal{L}_{a d v} =\lambda_{1} \mathcal{L}_{m m d}+\lambda_{2} \mathcal{L}_{d c}+\lambda_{3} \mathcal{L}_{\text {mixup }}  \quad\quad(6)$

　　关于对抗损失：

　　　　MMD 损失：$\mathcal{L}_{m m d}=\mathcal{L}_{r b f}\left(C\left(F_{s}\right), F_{T_{i}}, \sigma\right)    \quad\quad(7)$

　　　　线性差值域鉴别损失：$\mathcal{L}_{\text {mixup }}=\mathcal{L}_{C E}\left(D\left(F_{m}^{M}\right), L_{i}^{m}\right)  \quad\quad(8)$

　Note：

　　线性差值：

　　　　$F_{m}^{\text {factor }}=\lambda F_{s}+\sum_{i=1}^{n} \frac{1-\lambda}{n} F_{T_{i}}$

　　　　$F_{m}^{\text {concat }}=\left[\lambda F_{s}, \frac{1-\lambda}{n} F_{T_{1}}, \ldots, \frac{1-\lambda}{n} F_{T_{n}}\right]$

　　　　$.L_{m}^{\text {concat }}=[\lambda, 2 \frac{1-\lambda}{n}, \ldots, N \frac{1-\lambda}{n}]$

　　　　$F_{m}^{T}=\lambda F_{T_{1}}+(1-\lambda) F_{T_{2}}$

　　　　$L_{m}^{T}=\lambda L_{T_{1}}+(1-\lambda) L_{T_{2}} $