【Ural】1519. Formula 1

http://acm.timus.ru/problem.aspx?space=1&num=1519

题意：给一个n×m的棋盘，其中'.'是空白，'*'是障碍，求经过所有点的哈密顿回路的数目。（n,m<=12）

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
#define BIT(a,b) ((a)<<((b)<<1))
#define CLR(a,b) (a^=((a)&BIT(3,b)))
#define GET(a,b) (((a)>>((b)<<1))&3)
int n, m, lastx, lasty;
ll ans;
bool mp[12][12];

void print(int s) {
	for(int i=0; i<=m; ++i) { int k=GET(s, i); if(k==0) putchar('#'); if(k==1) putchar('('); if(k==2) putchar(')'); }
	puts("");
}
int find(int col, int flag, int s) {
	int ret, sum=0;
	if(flag==0) {
		for(int i=col; i>=0; --i) {
			int k=GET(s, i);
			if(k==1) --sum;
			if(k==2) ++sum;
			if(!sum) { ret=i; break; }
		}
	}
	else {
		for(int i=col; i<=m; ++i) {
			int k=GET(s, i);
			if(k==1) ++sum;
			if(k==2) --sum;
			if(!sum) { ret=i; break; }
		}
	}
	return ret;
}
bool getnext(int s, int row, int col, bool U, bool D, bool L, bool R, int &T, ll &sum) {
	if((col==0 && L) || (col==m-1 && R)) return 0;
	if((row==0 && U) || (row==n-1 && D)) return 0;
	if((D && mp[row+1][col]) || (R && mp[row][col+1])) return 0;
	if(row==lastx && col==lasty && (D || R)) return 0;
	int l=GET(s, col), u=GET(s, col+1), d=0, r=0;
	if((!l && L) || (!u && U) || (l && !L) || (u && !U)) return 0;
	T=s;
	// printf("s:"); print(s); printf("row:%d, col:%d, U:%d, D:%d, L:%d, R:%d", row, col, U, D, L, R);
	// printf(" \t 左插头:"); if(l==0) putchar('#'); if(l==1) putchar('('); if(l==2) putchar(')');
	// printf(" , 上插头:"); if(u==0) putchar('#'); if(u==1) putchar('('); if(u==2) putchar(')'); puts("");
	CLR(T, col);
	CLR(T, col+1);
	if(!l && !u) {
		if(D && R) d=1, r=2;
	}
	else if(l && u) {
		if(l==1 && u==1) {
			int pos=find(col+1, 1, s);
			CLR(T, pos);
			T|=BIT(1, pos);
		}
		else if(l==2 && u==2) {
			int pos=find(col, 0, s);
			CLR(T, pos);
			T|=BIT(2, pos);
		}
		else if(l==1 && u==2) {
			if(row!=lastx || col!=lasty) return 0;
			ans+=sum;
		}
	}
	else if(l && !u) {
		if(D) d=l, r=0;
		if(R) d=0, r=l;
	}
	else if(!l && u) {
		if(D) d=u, r=0;
		if(R) d=0, r=u;
	}
	T|=BIT(d, col);
	T|=BIT(r, col+1); if(col==m-1) T<<=2; //printf("t:"); print(T); puts("");
	return 1;
}

struct H {
	static const int M=1000007;
	struct E { int next, to; }e[M];
	int head, cnt;
	int hash[M];
	ll sum[M];
	H() { memset(hash, -1, sizeof hash); memset(sum, 0, sizeof sum); cnt=head=0; }
	bool find(int x, int &pos) {
		pos=x%M;
		while(1) { if(hash[pos]==x) return false; else if(hash[pos]==-1) break; ++pos; if(pos==M) pos=0; }
		hash[pos]=x;
		return true;
	}
	void ins(int t, ll d) { int pos; bool flag=find(t, pos); if(!flag) { sum[pos]+=d; return; } e[++cnt].next=head; head=cnt; e[cnt].to=pos; sum[pos]=d; }
	void clr() { for(int i=head; i; i=e[i].next) hash[e[i].to]=-1, sum[e[i].to]=0; head=0; cnt=0; }
}T1, T2;

#define dbg(x) cout << #x << " = " << x << endl
void bfs() {
	H *q[2]; q[0]=&T1, q[1]=&T2;
	q[0]->ins(0, 1);
	for(int row=0; row<n; ++row) for(int col=0; col<m; ++col) {
		q[1]->clr();
		for(int i=q[0]->head; i; i=q[0]->e[i].next) {
			ll sum=q[0]->sum[q[0]->e[i].to];
			int s=q[0]->hash[q[0]->e[i].to], t;
			if(mp[row][col]) {
				if(getnext(s, row, col, 0, 0, 0, 0, t, sum)) q[1]->ins(t, sum);
			}
			else {
				if(getnext(s, row, col, 1, 1, 0, 0, t, sum)) q[1]->ins(t, sum);
				if(getnext(s, row, col, 1, 0, 1, 0, t, sum)) q[1]->ins(t, sum);
				if(getnext(s, row, col, 1, 0, 0, 1, t, sum)) q[1]->ins(t, sum);
				if(getnext(s, row, col, 0, 1, 1, 0, t, sum)) q[1]->ins(t, sum);
				if(getnext(s, row, col, 0, 1, 0, 1, t, sum)) q[1]->ins(t, sum);
				if(getnext(s, row, col, 0, 0, 1, 1, t, sum)) q[1]->ins(t, sum);
			}
		}
		//printf("%d %d\n", row, col);
		//for(int i=q[1]->head; i; i=q[1]->e[i].next) printf("%d ", q[1]->e[i].to); puts("");
		swap(q[0], q[1]);
		if(row==lastx && col==lasty) return;
	}
}

int main() {
	scanf("%d%d", &n, &m);
	for(int i=0; i<n; ++i) for(int j=0; j<m; ++j) {
		char c=getchar(); while(c!='*'&&c!='.') c=getchar();
		if(c=='*') mp[i][j]=1;
		else lastx=i, lasty=j;
	}
	bfs();
	printf("%lld\n", ans);
	return 0;
}

　　

---

我的插头dp入门题...................

关于插头dp...我简单介绍一下....（具体看cdq论文《基于连通性状态压缩的动态规划问题》ppt和word最好都看）

首先我们逐格设状态，且记录轮廓线上插头的连通情况。

在本题中，我们按照从左往右，从上到下的顺序递推，而且每一个格子有且只有两个插头，可以发现，这样我们只需要考虑轮廓线上每个格子的m个下插头和1个右插头的连通情况即可（因为这就能表示当前格子的左插头和上插头）

而插头之间的连通性我们用状压解决，原理是括号序列（当然有很多种方法，还有一种是最小表示法，听说速度很慢就没看QAQ）：

首先本题要求的是回路，即路径不相交，这就提供了一个很好的性质，即性质1：

性质1：轮廓线上从左到右 4 个插头 a, b, c, d,如果 a, c 连通,并且与 b 不连通,那么 b, d 一定不连通，如图：

证明请看上边说的论文。

性质2：轮廓线上每一个连通分量恰好有 2 个插头

证明也是看论文....

然后这就能和括号序列一一对应，即每一个插头可以表示为：

0：表示没有插头，我们用'#'表示

1：表示插头是左括号，即'('

2：表示插头是有括号，即')'

因此我们对于每一个的状态，我们只需要记录：

1、轮廓线上的m个下插头和1个右插头

2、轮廓线上各个插头的连通情况（即括号序列）

而发现，状态1是可以包含在状态2内的，即当状态2中的插头对于的值是>=1的，说明就有插头。因此我们只需要记录下插头和右插头的连通情况（注意，上插头和左插头是不需要再表示了的，因为我们逐格转移的时候可以根据轮廓线上1个右插头得知左插头，一个下插头得知上插头）

而插头的连通情况我们只需要状压m+1个3进制位即可，为了效率，我们用4进制编码。（其中假如处理当前格的列是col，那么右插头的位置就是col+1）

然后我们现在来考虑状态转移（好麻烦啊...部分图片转自http://blog.sina.com.cn/s/blog_51cea4040100gmky.html）：

考虑当前格子(row, col)（考虑上下左右均不是障碍且自己也不是障碍），而且在(row, col-1)（或者(row-1, m)）这个轮廓线上的连通状态，我们用L表示右插头（即当前格点的左插头，位置就是col），U表示下插头（即当前格点的上插头，位置是col+1）

（在这里有个显然的技巧，我们每一次修改会修改col和col+1的状态，因此我们可以在转移时先将所有轮廓线上的连通情况直接赋值到下一个格点的轮廓线上

（在下边的讨论中，默认已经考虑了边界情况，即不费笔墨说需要边界处理的情况

1、L=0 && U=0：

此时新增了1个连通分类，如图：

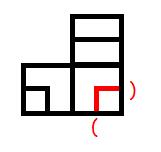
此时我们只能在当前格点放下插头和右插头，即将col的状态改为1，col+1的状态改为2，也就是

## -> ()

2、L!=0 && U!=0

此时col的状态改为0, col+1的状态改为0（因为并没有下插头和右插头，也就是

## -> ##

这个需要考虑四种情况.........即L和U分别取1和2

a、L=1 && U=1

这个图大概是这样的

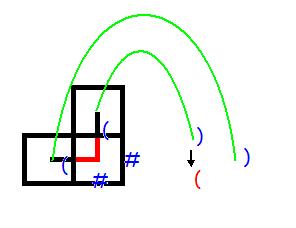
发现我们需要更改上插头所对应的插头的括号为2，即')'，我们O(n)处理一下就能得到

b、L=2 && U=2

如图：

发现我们只需要把左插头对应的插头改为2，即')'即可..

c、L=2 && U=1

此时如图：

不需要修改....

d、L=1 && U=2

如图：

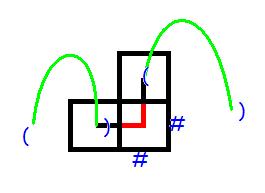
这种情况很特殊，因为如果一连上，就是一整条环了，因此只能是棋盘中最后一个可以放的格子

3、L=0 && U!=0 || L!=0 && U=0

这种情况直接判断当前要转移到的插头是下插头还是右插头即可

最后答案就是转移到2.d的方案数

怎么写呢....如果直接推....$O(nm2^{(m+1)*2})$直接跪....原因是太多无用状态....

那么我们考虑bfs拓展状态....然后hash判判重即可

这种做法复杂度还是一个迷...如何分析合法括号序列的数目.....

upd：听说和卡特兰数有关...的确...我们可以很容易得到sum{h(a)*h(n-a)}的方程....

upd：听说加了空格后和卡特兰数就没什么关系了................