C语言之走迷宫深度和广度优先（利用堆栈和队列）

完成以下迷宫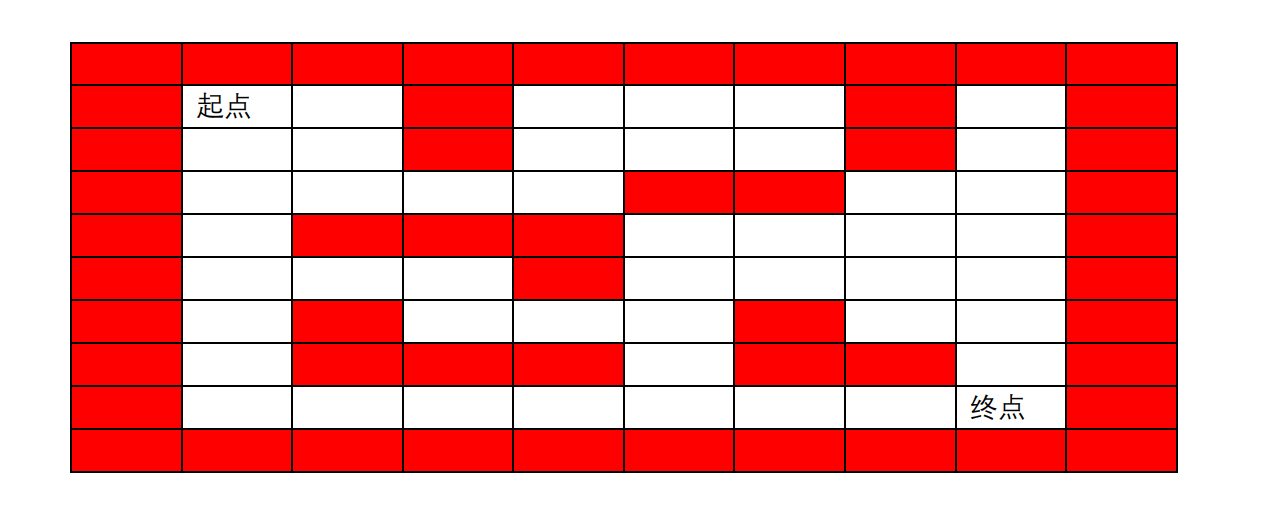

利用二维数组储存每一个数组里的值，若是不能走则为1，若是可行就是0，走过了就设为2。

一般是再复制一个数组，用来记录。

堆栈的思想就是将一个点的上下左右都遍历一遍，若可行进栈，跳出遍历，再寻找下一个可走的。若遇到无路可走的就退回上一步，就是出栈。所以就是说堆栈里记录的是可以走到终点的路。

队列的思想就是一直找，把所有可以走的路都走一遍，直到遇到终点。

这里的每一个可以走的点都为链表中的一个节点，在队列中要记录这个点的上一点是什么，就是哪一个点衍生出的这个点。

若是堆栈，最后在出栈便是所走的路径，但是堆栈是后进先出的原理，可能为了好看最后要做些处理。

若是队列，最后是利用找到的终点的那个节点，一直找这个节点的上一个节点，上个节点的上个节点，一直找到起点，可能为了好看最后还是要做些处理。

这里就是按照上述方法做的，但是太懒了，做出来就没有处理了。

堆栈是比较简单的，主要是队列中的头部和尾部的节点设置，和进队列的时候是怎么循环，这个循环是怎么在遍历之前的节点的也同时在加入新的节点进队。后来我是没有用出队这个原理去做。

以下是用堆栈实现的

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

#include<time.h>

typedef struct stack{

int x;//记录下标

int y;

int direction;//记录方向

struct stack *next;

}stack;

int main(){

int maze[10][10];

int i,j;

for(i=0;i<10;i++){

for(j=0;j<10;j++){

if(i==0 || j==0 || i==9|| j==9){

maze[i][j]=1;

} else{

maze[i][j]=0;

}

}

}

maze[1][3]=1;

maze[1][7]=1;

maze[2][3]=1;

maze[2][7]=1;

maze[3][5]=1;

maze[3][6]=1;

maze[4][2]=1;

maze[4][3]=1;

maze[4][4]=1;

maze[5][4]=1;

maze[6][2]=1;

maze[6][6]=1;

maze[7][2]=1;

maze[7][3]=1;

maze[7][4]=1;

maze[7][6]=1;

maze[7][7]=1;

maze[8][1]=1;

//这里是输进去的迷宫，也可以随机实现，但是这里偷下懒

int cmaze[10][10];

for(i=0;i<10;i++){

for(j=0;j<10;j++){

cmaze[i][j]=maze[i][j];

}

}

//用一个新的二维数组记录走过的点

printf("\n\n");

stack *top,*p,*q,*t,*s;

top=(stack *)malloc(sizeof(stack));

top->next=NULL;

//人为设置的，(1,1)是起点，（8，8）是终点

int flag=0,x=0,y=0;

if(flag==0){

p=(stack *)malloc(sizeof(stack));

p->x=1;

p->y=1;

p->direction=-1;

q=top->next;

top->next=p;

p->next=q;

flag=1;

}

q=top->next;

x=q->x;

y=q->y;

while(q->x!=8 || q->y!=8){

　　//0:向左 y+1 1:向下 x+1 2:向右 y-1 3:向上 x+1

if(cmaze[x][y+1]==0){

p=(stack *)malloc(sizeof(stack));

p->x=x;

p->y=y+1;

p->direction=0;

q=top->next;

top->next=p;

p->next=q;

cmaze[x][y+1]=2;

}else if(cmaze[x+1][y]==0){

p=(stack *)malloc(sizeof(stack));

p->x=x+1;

p->y=y;

p->direction=1;

q=top->next;

top->next=p;

p->next=q;

cmaze[x+1][y]=2;

}else if(cmaze[x][y-1]==0){

p=(stack *)malloc(sizeof(stack));

p->x=x;

p->y=y-1;

p->direction=2;

q=top->next;

top->next=p;

p->next=q;

cmaze[x][y-1]=2;

}else if(cmaze[x+1][y]==0){

p=(stack *)malloc(sizeof(stack));

p->x=x;

p->y=y-1;

p->direction=3;

q=top->next;

top->next=p;

p->next=q;

cmaze[x+1][y]=2;

}else{

t=top->next;

s=t->next;

top->next=s;

free(t);

}

q=top->next;

x=q->x;

y=q->y;

//每次都是栈顶的元素找方向，找不到就是free掉，出栈，就是后退一步

}

for(i=0;i<10;i++){

for(j=0;j<10;j++){

printf(" %d",cmaze[i][j]);

}

printf("\n");

}

printf("溯源：\n");

while(top->next!=NULL){

p=top->next;

x=p->x;

y=p->y;

printf("x=%d,y=%d\n",x,y);

top=top->next;

}

return 0;

}

//队列

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

#define maxsize 10

#define null 0

typedef struct node{

int x;

int y;

struct node*last;

struct node*next;

} lqnode;

typedef struct{

node *front,*rear;

}Queue;

//定义一个队列的结构体，记录头和尾

int main(){

int maze[10][10];

int i,j;

for(i=0;i<10;i++){

for(j=0;j<10;j++){

if(i==0 || j==0 || i==9|| j==9){

maze[i][j]=1;

} else{

maze[i][j]=0;

}

}

}

maze[1][3]=1;

maze[1][7]=1;

maze[2][3]=1;

maze[2][7]=1;

maze[3][5]=1;

maze[3][6]=1;

maze[4][2]=1;

maze[4][3]=1;

maze[4][4]=1;

maze[5][4]=1;

maze[6][2]=1;

maze[6][6]=1;

maze[7][2]=1;

maze[7][3]=1;

maze[7][4]=1;

maze[7][6]=1;

maze[7][7]=1;

maze[8][1]=1;

for(i=0;i<10;i++){

for(j=0;j<10;j++){

printf(" %d",maze[i][j]);

}

printf("\n");

}

Queue *q;

lqnode *p;

q=(Queue *)malloc(sizeof(Queue));

p=(lqnode *)malloc(sizeof(lqnode));

p->next=null;

q->rear=p;

q->front=p;

int x,y;

lqnode *r,*t;

r=(lqnode *)malloc(sizeof(lqnode));

r->x=1;

r->y=1;

r->last=null;

q->rear->next=r;

r->next=null;

q->rear=r;

t=q->front->next;

x=t->x;

y=t->y;

printf("可以走的点\n");

while(x!=8 || y!=8){

if(maze[x][y+1]==0){

r=(lqnode *)malloc(sizeof(lqnode));

r->x=x;

r->y=y+1;

r->last=t;

q->rear->next=r;

r->next=null;

q->rear=r;

maze[x][y+1]=2;

}

if(maze[x+1][y]==0){

r=(lqnode *)malloc(sizeof(lqnode));

r->x=x+1;

r->y=y;

r->last=t;

q->rear->next=r;

r->next=null;

q->rear=r;

maze[x+1][y]=2;

}

if(maze[x][y-1]==0){

r=(lqnode *)malloc(sizeof(lqnode));

r->x=x;

r->y=y-1;

r->last=t;

q->rear->next=r;

r->next=null;

q->rear=r;

maze[x][y-1]=2;

}

if(maze[x+1][y]==0){

r=(lqnode *)malloc(sizeof(lqnode));

r->x=x+1;

r->y=y;

r->last=t;

q->rear->next=r;

r->next=null;

q->rear=r;

maze[x+1][y]=2;

}

//可以走的就加入队列，然后队列是从头开始循环的，一边循环一边加入了新元素

t=t->next;

x=t->x;

y=t->y;

printf("%d,%d\n",x,y);

}

printf("溯源：\n");

while(t->last!=NULL){

printf("x=%d,y=%d\n",t->x,t->y);

t=t->last;

}

//用last记录每一个节点是由哪个节点走过来的

return 0;

}

1 1 1 1 是上面的迷宫，截图没有截好