二十一、B树的定义、查找、插入和删除

一、B树的定义

一棵m阶的B树，或为空树，或为满足下列特性的m叉树：

（1）树中每个结点至多有m棵子树；
（2）B树是所有结点的平衡因子均等于0的多路平衡查找树；
（3）若根结点不是叶子结点，则至少有两棵子树；
（4）除根之外的所有非终端结点至少有⌈m/2⌉棵子树；
（5）所有的叶子结点都出现在同一层次上，并且不带信息，通常称为失败结点（失败结点并不存在，指向这些结点的指针为空。引入失败结点是为了便于分析B树的查找性能）；
（6）所有的非终端结点最多有m-1个关键字，结点的结构如图所示。

其中：

• ${K_i}(i = 1,...,n)$ 为关键字，且 ${K_i} < {K_{i + 1}}(i = 1,...,n - 1)$。
• ${P_i}(i = 0,...,n)$ 为指向子树根结点的指针，且指针 ${P_{i - 1}}$ 所指子树中所有结点的关键字均小于 ${K_i}(i = 1,...,n)$ ， ${P_{n}}$ 所指子树中所有结点的关键字均大于 ${K_{n}}$。
• $n(\left\lceil {m/2} \right\rceil  - 1 \le n \le m - 1)$ 为关键字的个数(或 $n+1$ 为子树个数）。

从上述定义可以看出，对任一关键字 ${K_i}$ 而言， ${P_{i - 1}}$ 相当于指向其“左子树”， ${P_{i}}$ 相当于指向其“右子树”。
B树具有平衡、有序、多路的特点。

二、B树的查找

  B树的查找从根结点开始，重复以下过程：若给定关键字等于结点中某个关键字K_i，则查找成功；若给定关键字比结点中的K₁小，则进入指针A₀。指向的下一层结点继续查找；若在两个关键字K_i-1和K_i之间，则进入它们之间的指针A_i-1从一指向的下一层结点继续查找；若比该结点所有关键字大，则在其最后一个指针A_n指向的下一层结点继续查找；若查找到叶子结点，则说明给定值对应的数据记录不存在，查找失败。

查看代码

#define m 3                     //B树的阶
typedef struct BTNode
{
    int keynum;                //结点当前关键字个数
    KeyType key[m+1];          //关键字数组,key[0]未用
    struct BTNode *parent;     //双亲结点指针
    struct BTNode *ptr[m+1];   //孩子结点指针数组
    Record *recptr[m+1];       //记录指针向量,0号单元未用
}BTNode, *BTree;

typedef struct
{
    BTree pt;                   //指向找到的结点
    int i;                      //1<=i<=m,在结点中的关键字位序
    int tag;                    //1:查找成功;0:查找失败
}Result;

int Search(BTree p,int key)
{   //在p->key[1...p->keynum]找k
    int i=1;
    while(i<=p->keynum && k>p->key[i]) i++;
    return i;
}

Result SearchBTree(BTree T,KeyType key)
{   //在m阶B树T上查找关键字key,返回结果(pt,i,tag)
    //若查找成功,则特征值tag=1,指针pt所指结点中第i个关键字等于key
    //否则特征值tag=0,等于key的关键字应插在指针pt所指结点中第i和第i+1个关键字之间
    int i=0;
    int found=FALSE;
    BTree p=T;
    BTree q=NULL;               //初始化,p指向待查结点,q指向p的双亲
    while(p && !found)
    {
        i=Search(p,key);        //在p->key[1...keynum]中查找i,使得:p->key[i]<=key<p->key[i+1]
        if(i>0 && p->key[i]==k)
            found=TRUE;         //找到待查关键字
        else
        {
            q=p;
            p=p->ptr[i];
        }
    }
    if(found)
        return (p,i,1);         //查找成功
    else
        return (q,i,0);         //查找不成功，返回K的插入位置信息
}

三、B树的插入

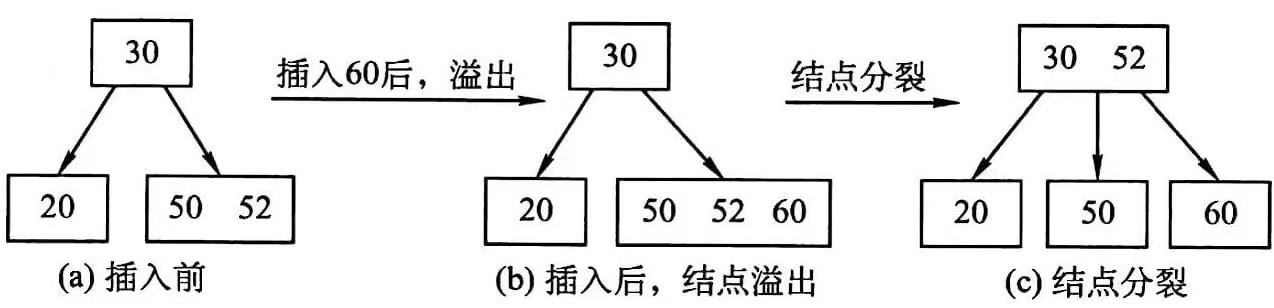
  B树的插入过程可描述为，利用B树的查找操作查找关键字k的插入位置。若找到，则说明该关键字已经存在，直接返回；否则查找操作必失败于某个最底层的非终端结点上，在该结点插入后，若其关键字总数n未达到m，算法结束，否则需分裂结点。

  分裂的方法是，生成一新结点，从中间位置把结点（不包括中间位置的关键字）分成两部分。前半部分留在旧结点中，后半部分复制到新结点中，中间位置的关键字连同新结点的存储位置插入到父结点中。如果插入后父结点的关键字个数也超过m-1，则继续分裂。这个向上分裂过程如果持续到根结点，则会产生新的根结点。

结点分裂示例

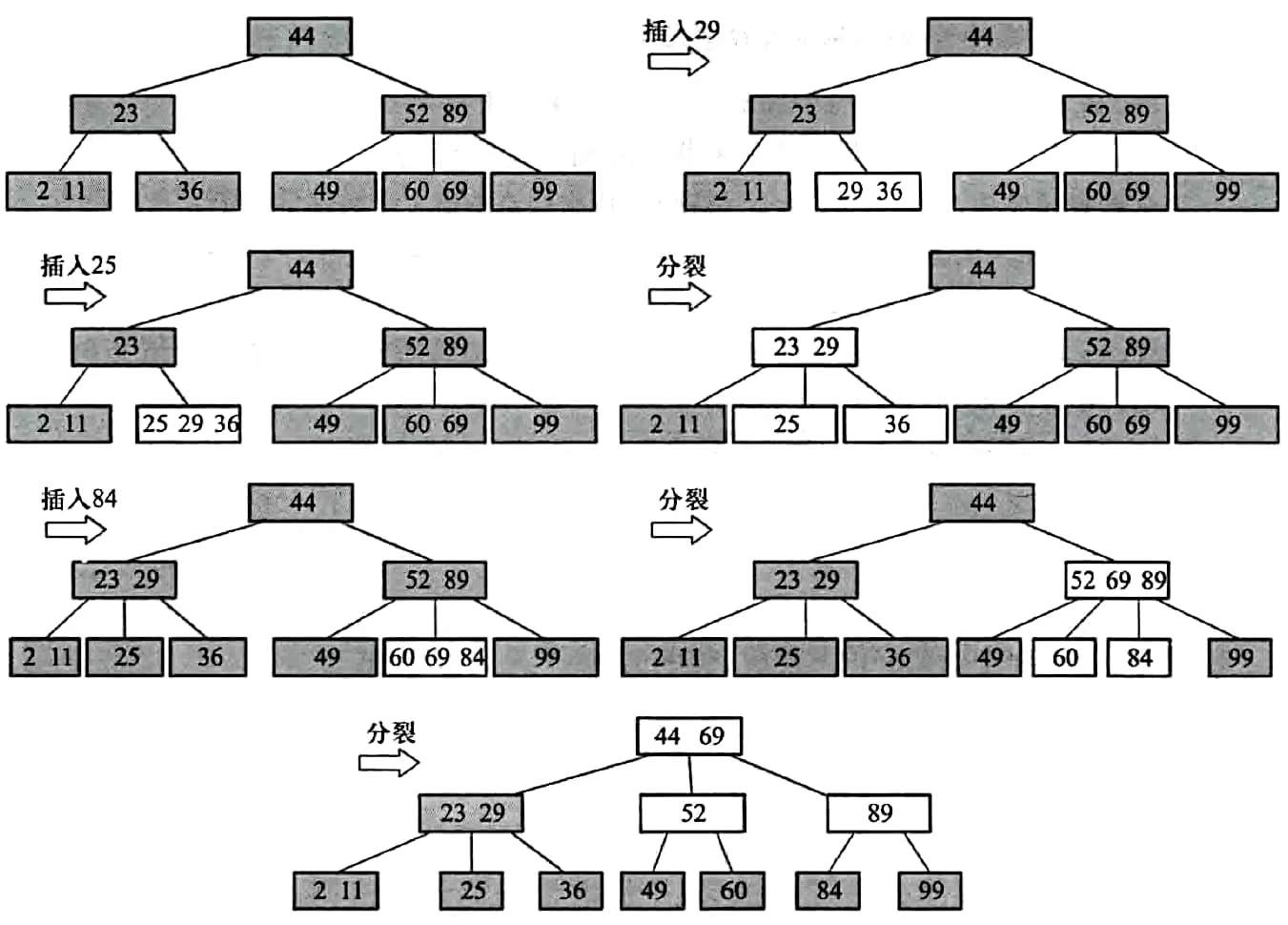
B树的插入动图示例

三阶B树插入示例

 void split(BTree& q, int s, BTree& ap)
{   //将q结点分裂成两个结点,前一半保留在原节点,后一半移入ap所指新结点
    int i = 0;
    int j = 0;
    int n = q->keynum;
    ap = (BTNode*)malloc(sizeof(BTNode));     //生成新结点
    ap->ptr[0] = q->ptr[s];
    for (i = s + 1, j = 1; j <= n; i++, j++)
    {   //后一半移入ap结点
        ap->key[j] = q->key[i];
        ap->ptr[j] = q->ptr[i];
    }
    ap->keynum = n - s;
    ap->parent = q->parent;
    for (i = 0; i <= n - s; i++)                        //修改新结点的子节点的parent域
    {
        if (ap->ptr[i] != NULL)
        {
            ap->ptr[i]->parent = ap;
        }
        q->keynum = s - 1;                              //q结点的前一半保留,修改keynum
    }
}

void newRoot(BTree& t, BTree p, int x, BTree ap)
{   //生成新的根节点
    t = (BTNode*)malloc(sizeof(BTNode));
    t->keynum = 1;
    t->ptr[0] = p;
    t->ptr[1] = ap;
    t->key[1] = x;
    if (p != NULL)
        p->parent = t;
    if (ap != NULL)
        ap->parent = t;
    t->parent = NULL;           //新根的双亲是空指针
}

void Insert(BTree& q, int i, int x, BTree ap)
{   //关键字x和新结点指针ap分别插入到q->key[i]和q->ptr[i]
    int j = 0;
    int n = q->keynum;
    for (j = n; j >= i; j--)
    {
        q->key[j + 1] = q->key[j];
        q->ptr[j + 1] = q->ptr[j];
    }
    q->key[i] = x;
    q->ptr[i] = ap;
    if (ap != NULL)
        ap->parent = q;
    q->keynum++;
}

void InsertBTree(BTree& t, int k, BTree q, int i)
{   //在B树t中q结点的key[i-1]和key[i]之间插入关键字k
    //若插入后结点关键字个数等于B树的阶,则沿双亲指针链进行结点分裂,使t仍是m阶B树
    int x = 0;
    int s = 0;
    int finished = 0;
    int needNewRoot = 0;
    BTree ap;
    if (!q)
        newRoot(t, NULL, k, NULL);          //生成新的根节点
    else
    {
        x = k;
        ap = NULL;
        while (needNewRoot == 0 && finished == 0)
        {
            Insert(q, i, x, ap);            //x和ap分别插入到q->key[i]和q->ptr[i]
            if (q->keynum < m)
                finished = 1;               //插入完成
            else
            {   //分裂q结点
                s = (m + 1) / 2;
                split(q, s, ap);
                x = q->key[s];
                if (q->parent != NULL)
                {
                    q = q->parent;
                    i = Search(q, x);      //在双亲结点中查找x的插入位置
                }
                else
                    needNewRoot = 1;
            }
        }
        if (needNewRoot == 1)                //t是空树或者根结点已分裂为q和ap结点
            newRoot(t, q, x, ap);              //生成含信息(q,x,ap)的新的根节点t
    }
}

四、B树的删除