torch.optim.SGD参数详解

随机梯度下降法

　　　　$\theta_{t} \leftarrow \theta_{t-1}-\alpha g_{t}$

Code：

optimzer = torch.optim.SGD(model.parameters(),lr = 0.001)

权重衰减

　　　　$\theta_{t} \leftarrow(1-\beta) \theta_{t-1}-\alpha \mathbf{g}_{t}$
　　其中 $\mathrm{g}_{t}$ 为第 $t$ 步更新时的梯度, $\alpha$ 为学习率, $\beta$ 为权重衰减系数，一般取值比较 小，比如 0.0005。

　　

Code：

optimzer = torch.optim.SGD(model.parameters(),lr = 0.001,weight_decay=0.0005)

动量法

　　动量（Momentum）是模拟物理中的概念．一个物体的动量指的是该物体 在它运动方向上保持运动的趋势，是该物体的质量和速度的乘积．动量法（Momentum Method）是用之前积累动量来替代真正的梯度．每次迭代的梯度可以 看作加速度． 在第 $t$ 次迭代时，计算负梯度的“加权移动平均”作为参数的更新方向，

　　　　$\Delta \theta_{t}=\rho \Delta \theta_{t-1}-\alpha g_{t}=-\alpha \sum\limits_{\tau=1}^{t} \rho^{t-\tau} g_{\tau}$

　　

Code：

optimzer = torch.optim.SGD(model.parameters(),lr = 0.001,momentum =0.001,dampening=0.001)

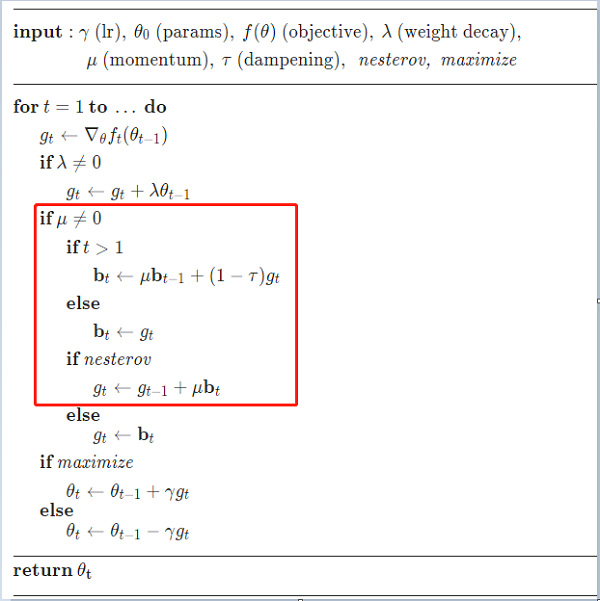
Nesterov加速梯度

　　 Nesterov 加速梯度（Nesterov Accelerated Gradient，NAG）是一种对动量 法的改进[Nesterov, 2013; Sutskever et al., 2013]，也称为Nesterov动量法（Nesterov Momentum）

　　在动量法中, 实际的参数更新方向  $\Delta \theta_{t}$  为上一步的参数更新方向  $\Delta \theta_{t-1}$  和当 前梯度的反方向 $ -g_{t}$  的叠加. 这样,  $\Delta \theta_{t}$  可以被拆分为两步进行, 先根据  $\Delta \theta_{t-1}$  更 新一次得到参数 $ \hat{\theta}$ , 再用 $ -g_{t}$  进行更新.

　　这样，合并后的更新方向为

　　　　$\Delta \theta_{t}=\rho \Delta \theta_{t-1}-\alpha \mathfrak{g}_{t}\left(\theta_{t-1}+\rho \Delta \theta_{t-1}\right)$

　　其中 $\mathfrak{g}_{t}\left(\theta_{t-1}+\rho \Delta \theta_{t-1}\right)$  表示损失函数在点 $\hat{\theta}=\theta_{t-1}+\rho \Delta \theta_{t-1}$ 上的偏导数.

　　

　　

Code：

optimzer = torch.optim.SGD(model.parameters(),lr = 0.001,momentum =0.001,nesterov=0.01)