论文解读（GCC）《Efficient Graph Convolution for Joint Node RepresentationLearning and Clustering》

论文信息

论文标题：Efficient Graph Convolution for Joint Node RepresentationLearning and Clustering
论文作者：Chakib Fettal, Lazhar Labiod,Mohamed Nadif
论文来源：2021, WSDM
论文地址：download
论文代码：download

1 Introduction

　　一个统一的框架中解决了节点嵌入和聚类问题。

2 Method

　　整体框架：

　　

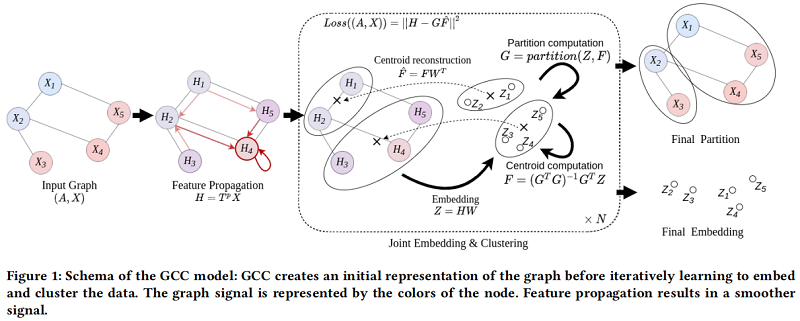
2.1 Joint Graph Representation Learning and Clustering

　　将同时进行的节点嵌入和聚类问题表述如下

　　　　$\begin{array}{l}&\underset{\theta_{1}, \theta_{2}, \mathbf{G}, \mathbf{F}}{\text{ min }} &\;\;\underbrace{\left\|\operatorname{dec}_{\theta_{2}}\left(\operatorname{enc}_{\theta_{1}}(\operatorname{agg}(\mathbf{A}, \mathbf{X}))\right)-\operatorname{agg}(\mathbf{A}, \mathbf{X})\right\|^{2}}_{\text {reconstruction term }}+\alpha \underbrace{\left\|\operatorname{enc}_{\theta_{1}}(\operatorname{agg}(\mathrm{A}, \mathrm{X}))-\mathrm{GF}\right\|^{2}}_{\text {clustering regularization term }}\\&\text { s.t. }& \mathrm{G} \in\{0,1\}^{n \times k}, \mathbf{G 1}_{k}=\mathbf{1}_{n}\end{array}\quad\quad(1)$

　　其中：

• • $\mathrm{G} \in\{0,1\}^{n \times k}$ 是二值分类矩阵；
  • $\mathbf{F} \in \mathbb{R}^{k \times d}$ 在嵌入空间中发挥质心的作用；
  • $\alpha$ 是调节寻求重构和聚类之间权衡的系数；

　　注意，聚类正则化器是编码观测值上的均值聚类损失[25]。它惩罚不导致聚类友好表示的变换。

2.2 Linear Graph Embedding

　　Encoder 类似 Linear graph autoencoders (LGAE) [33] ，本文提出：

　　　　$Z=\operatorname{enc}\left(\operatorname{agg}(\mathbf{A}, \mathbf{X}) ; \mathbf{W}_{1}\right)=\operatorname{agg}(\mathbf{A}, \mathbf{X}) \mathbf{W}_{1}$

　　Decoder 即一个简单的线性变换：

　　　　$\operatorname{dec}\left(\mathbf{Z} ; \mathbf{W}_{2}\right)=\mathbf{Z} \mathbf{W}_{2}$

2.3 Normalized Simple Graph Convolution

　　本文的聚合函数受到 SGC [42] 中提出的简单图卷积的启发。设为：

　　　　$\operatorname{agg}(\mathbf{A}, \mathbf{X})=\mathbf{T}^{p} \mathbf{X}$

　　其中，$T$ 不是添加了自环的对称标准化邻接矩阵，本文 $T$  定义为 ：

　　　　$\mathrm{T}=\mathrm{D}_{\mathrm{T}}^{-1}(\mathrm{I}+\tilde{\mathrm{S}})$

　　其中：

• • $\tilde{\mathrm{S}}=\tilde{\mathbf{D}}^{-1 / 2} \tilde{\mathrm{A}} \tilde{\mathrm{D}}^{-1 / 2}$；
  • $\tilde{\mathrm{A}}=\mathrm{A}+\mathrm{I}$；
  • $\tilde{\mathbf{D}}$ 是从 $\tilde{\mathrm{A}}$ 得出的度矩阵；
  • $\mathrm{D}_{\mathrm{T}}$ 是从 $I + \tilde{\mathrm{S}}$ 得出的度矩阵；

　　GCN 的频率响应函数 $p(\lambda)=1-\tilde{\lambda}_{i} \in[-1,1)$。

　　SGC 的传播矩阵为 $\mathbf{I}-\tilde{\mathbf{S}}=\mathbf{I}-\tilde{\mathbf{D}}^{-1 / 2}(\mathbf{I}-\tilde{\mathbf{L}}) \tilde{\mathbf{D}}^{-1 / 2}$，其频率响应函数为 $h\left(\tilde{\lambda}_{l}\right)=1-\tilde{\lambda}_{l} $，该滤波器在 $[0,1]$ 上是低通的，而不是 $[0,1.5]$。然后，本文建议进一步添加自循环和行规范化矩阵 $\tilde{\mathrm{S}}$。这将产生以下影响

• • 从谱域的角度来看：所提出的归一化进一步缩小了矩阵的谱域到 $[0,1]$ 中，如图2所示，这使得滤波器真正的低通；
  • 从空间域的角度来看：每个转换后的顶点成为邻居的加权平均值，这更直观，但它也考虑了列度信息，不像直接随机游走邻接归一化；

　　本文的问题变成：

　　　　$\begin{array}{l}&\underset{\mathrm{G}, \mathbf{F}, \mathbf{W}_{1}, \mathbf{W}_{2}}{\text{min }}  &\left\|\mathbf{T}^{p} \mathbf{X}-\mathbf{T}^{p} \mathbf{X} \mathbf{W}_{1} \mathbf{W}_{2}\right\|^{2}+\alpha\left\|\mathbf{T}^{p} \mathbf{X} \mathbf{W}_{1}-\mathrm{GF}\right\|^{2} \\&\text { s.t. } &\mathrm{G} \in\{0,1\}^{n \times k}, \mathbf{G 1}_{k}=\mathbf{1}_{n}\end{array}$

　　前项代表自编码器重构作用，后项代表嵌入空间聚类的作用。本文对于权重系数取相等（$\alpha =1$）。

2.5 Graph Convolutional Clustering

　　为使得嵌入空间信息和聚类信息相互补充，本文设置 $\mathrm{W}=\mathrm{W}_{1}=\mathrm{W}_{2}^{\top}$，并添加一个正交性约束，所以 $Eq.4$ 变为：

　　　　$\begin{array}{l}\underset{\mathrm{G}, \mathrm{F}, \mathbf{W}}{\text{min }}&\left\|\mathrm{T}^{p} \mathbf{X}-\mathbf{T}^{p} \mathbf{X W W}{ }^{\top}\right\|^{2}+\left\|\mathrm{T}^{p} \mathbf{X W}-\mathrm{GF}\right\|^{2} \\\text { s.t. } & \mathrm{G} \in\{0,1\}^{n \times k}, \mathbf{G} \mathbf{1}_{k}=\mathbf{1}_{n}, \mathbf{W}^{\top} \mathbf{W}=\mathbf{I}_{k}\end{array}\quad\quad\quad(5)$

　　与 [43] 类似，该问题等价于

　　　　$\begin{array}{l}\underset{\mathrm{G}, \mathrm{F}, \mathbf{W}}{\text{min }}&\left\|\mathrm{T}^{p} \mathbf{X}-\mathrm{GFW}^{\top}\right\|^{2} \\\text { s.t. } & \mathrm{G} \in\{0,1\}^{n \times k}, \mathbf{G} \mathbf{1}_{k}=\mathbf{1}_{n}, \mathbf{W}^{\top} \mathbf{W}=\mathbf{I}_{k}\end{array}\quad\quad\quad(6)$

证明：

　　首先分解重构项：

　　　　$\begin{aligned}\left\|\mathbf{T}^{p} \mathbf{X}-\mathbf{T}^{p} \mathbf{X W} \mathbf{W}^{\top}\right\|^{2} &=\left\|\mathbf{T}^{p} \mathbf{X}\right\|^{2}+\left\|\mathbf{T}^{p} \mathbf{X W} \mathbf{W}^{\top}\right\|^{2}-2\left\|\mathbf{T}^{p} \mathbf{X W}\right\|^{2} \\&=\left\|\mathbf{T}^{p} \mathbf{X}\right\|^{2}-\left\|\mathbf{T}^{p} \mathbf{X W}\right\|^{2} \quad \text { due to } \mathbf{W}^{\top} \mathbf{W}=\mathbf{I}_{k}\end{aligned}$

　　其次，聚类正则化项分解为：

　　　　$\left\|\mathrm{T}^{p} \mathrm{XW}-\mathrm{GF}\right\|^{2}=\left\|\mathrm{T}^{p} \mathrm{XW}\right\|^{2}+\|\mathrm{GF}\|^{2}-2 \operatorname{Tr}\left(\left(\mathrm{T}^{p} \mathrm{XW}\right)^{\top} \mathrm{GF}\right)$

　　上述两个结果表达式求和：

　　　　$\begin{array}{r}\left\|\mathbf{T}^{p} \mathbf{X}\right\|^{2}+\|\mathrm{GF}\|^{2}-2 \operatorname{Tr}\left(\left(\mathrm{T}^{p} \mathrm{XW}\right)^{\top} \mathrm{GF}\right)=\left\|\mathrm{T}^{p} \mathrm{X}-\mathrm{GFW}^{\top}\right\|^{2} \\\text { due to }\left\|\mathrm{GFW}{ }^{\top}\right\|=\|\mathrm{GF}\|\end{array}$

　　因此，优化 $\text{Eq.5}$ 等价于优化 $\text{Eq.6}$。

3 Optimization and algorithm

　　该算法交替固定 $F$、$G$ 和 $W$ 中两个矩阵 ，并求解第三个矩阵。

3.1 Optimization Procedure

Initialization

　　对 $\mathbf{T}^{p} \mathbf{X}$ 应用主成分分析(PCA) 得到的前 $f$ 个分量来初始化 $\mathbf{W}$。然后在 $\mathbf{T}^{p} \mathbf{X}$ 上应用 k-means 得到 $\mathbf{F}$ 和 $\mathrm{G}$。

Update Rule for $\mathbf{F}$

　　通过固定 $\mathrm{G}$ 和 $\mathrm{W}$ 并求解 $\mathbf{F}$，我们得到了一个线性最小二乘问题。通过将导数设为零，得到了对给定问题的最优解的正态方程。然后是更新规则

　　　　$\mathbf{F}=\left(\mathrm{G}^{\top} \mathrm{G}\right)^{-1} \mathrm{G}^{\top} \mathrm{T}^{p} \mathbf{X W}\quad\quad\quad(7)$

　　直观地说，每个行向量 $\mathrm{f}_{i}$ 被设置为分配给集群 $i$ 的嵌入 $\mathrm{XW}$ 的平均值。并通过 K-means 更新质心矩阵。

Update Rule for $\mathbf{W}$

　　固定 $Eq.6$ 中的 $\mathrm{F}$ 和 $\mathrm{G}$，所以更新规则如下：

　　　　$\mathbf{W}=\mathbf{U V}^{\top} \quad \text { s.t. } \quad[\mathrm{U}, \Sigma, \mathrm{V}]=\operatorname{SVD}\left(\left(\mathrm{T}^{p} \mathbf{X}\right)^{\top} \mathrm{GF}\right)$

　　其中，

• • $\Sigma=\left(\sigma_{i i}\right)$　　
  • $U$ 和 $V$ 分别代表 $\left(\mathrm{T}^{p} \mathbf{X}\right)^{\top} \mathrm{GF}$ 的特征值和左、右特征向量；

　　固定 $F$ 和 $G$ 产生如下问题：

　　　　$\underset{\mathrm{W}}{\text{min }}\left\|\mathrm{T}^{p} \mathrm{X}-\mathrm{GFW}^{\top}\right\|^{2} \quad \text { s.t. } \quad \mathbf{W}^{\top} \mathbf{W}=\mathbf{I}_{k} .$

　　因为：$\left\|\mathbf{T}^{p} \mathbf{X}-\mathbf{G F W}^{\top}\right\|^{2}=\left\|\mathbf{T}^{p} \mathbf{X}\right\|^{2}+\left\|\mathbf{G F W}^{\top}\right\|^{2}-2 \operatorname{Tr}\left(\mathbf{W F}^{\top} \mathbf{G}^{\top} \mathbf{T}^{p} \mathbf{X}\right)$ 和 $\left\|\mathrm{GFW}^{\top}\right\|^{2}=\|\mathrm{GF}\|^{2}$，所以 $\text{Eq.9}$ 等价于

　　　　$\underset{\mathbf{W}}{\text{max}}\operatorname{Tr}\left(\mathbf{W F}^{\top} \mathbf{G}^{\top} \mathbf{T}^{p} \mathbf{X}\right) \quad \text { s.t. } \quad \mathbf{W}^{\top} \mathbf{W}=\mathbf{I}_{k} .$

　　由于 $[\mathrm{U}, \Sigma, \mathrm{V}]=\operatorname{SVD}\left(\mathbf{F}^{\top} \mathbf{G}^{\top} \mathrm{T}^{p} \mathrm{X}\right)$，所以有

　　　　$\begin{aligned}\operatorname{Tr}\left(\mathbf{W F}^{\top} \mathbf{G}^{\top} \mathbf{T}^{p} \mathbf{X}\right) &=\operatorname{Tr}\left(\mathbf{W} \mathbf{U} \Sigma \mathbf{V}^{\top}\right) \\&=\sum\limits_{i=1}^{f} \sigma_{i i}<\mathbf{w}_{i}^{\prime} \mathbf{U}, \mathbf{v}_{i}^{\prime}>\\& \leq \sum\limits_{i=1}^{f} \sigma_{i i}\left\|\mathbf{w}_{i}^{\prime} \mathbf{U}\right\| \times\left\|\mathbf{v}_{i}^{\prime}\right\|=\sum\limits_{i=1}^{f} \sigma_{i i}=\operatorname{Tr}(\Sigma)\end{aligned}$

　　这意味着当 $\operatorname{Tr}\left(\mathbf{W U \Sigma V ^ { \top }}\right)=\operatorname{Tr}(\Sigma)$ 或当 $\mathbf{V}^{\top} \mathbf{W U}=  I$ 时达到了 $Eq.9$ 的上界，即在 $\mathbf{W}=\mathbf{V U}^{\top} $ 时达到了最大值。

Update Rule for G

　　通过固定 $F$ 和 $W$ 并求解 $F$，我们得到了一个可以通过 k-means 算法的分配步骤进行优化的问题。那么，更新规则定为

　　　　$g_{i j^{*}} \leftarrow\left\{\begin{array}{ll}1 & \text { if } j^{*}=\arg \min _{j}\left\|\left(\mathbf{T}^{p} \mathbf{X W}\right)_{i}-\mathbf{f}_{j}\right\|^{2} \\0 & \text { otherwise. }\end{array}\right.\quad\quad\quad(10)$

3.2 The GCC Algorithm

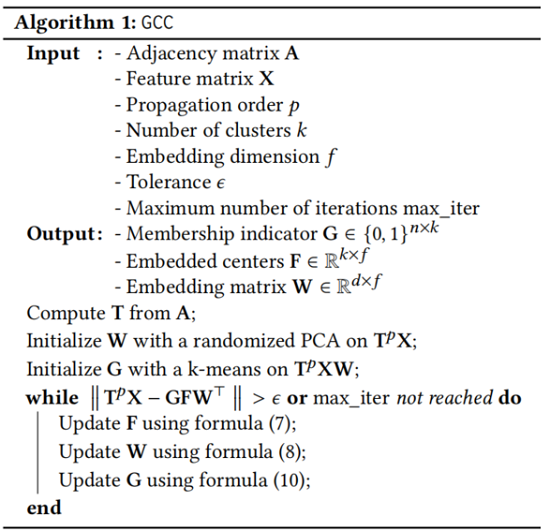
　　算法步骤如 Algorithm 1 所示：

　　

　　传播阶 $p$ 的选择对算法的整体性能非常重要。较小的 $p$ 可能意味着传播的邻域信息不足，而较大的 $p$  可能导致图信号的过度平滑。Figure 3 显示了使用 t-SNE 算法[39]对不同 $p$ 值的 Cora 数据集的投影。

　　

　　对于 $p$ 的选择如 Algorithm 2 所示：

　　

4 Experiments

数据集

　　

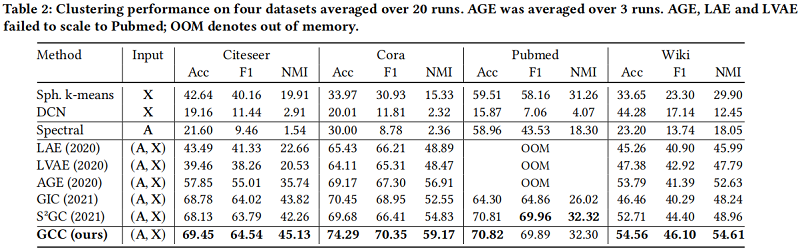
聚类结果

　　

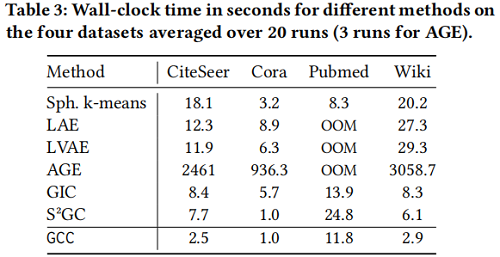
运行时间

　　

5 Conclusion

　　在本文中，我们利用图卷积网络的简单公式，得到了一个有效的模型，在一个统一的框架中解决了节点嵌入和聚类问题。首先，我们提供了一个归一化，使GCN编码器在严格意义上充当低通滤波器。其次，我们提出了一种新的方法，其中需要优化的目标函数利用了来自GCN嵌入重建损失和这些嵌入的簇结构的信息。第三，我们推导了复杂性被严格研究的GCC。在此过程中，我们展示了GCC如何以更有效的方式比其他图聚类算法获得更好的性能。请注意，所有比较的方法在本质上都是无监督的，以便与我们的模型进行公平的比较。我们的实验证明了我们的方法的兴趣。我们还展示了GCC是如何与其他方法相关的，包括一些GCN变体。

　　该模型是一种灵活的模型，可以从多个方向进行扩展，为今后的研究提供了机会。例如，在我们的方法中，我们假设调节寻求重建和聚类之间的权衡的 $\alpha$ 系数等于1，研究这个值的选择将是很有趣的。另一方面，虽然我们这项工作的重点是聚类，但值得将问题扩展到这样的，例如，协同聚类，这在文档聚类等许多现实场景中是有用的。

修改历史

2022-06-27 创建文章

论文解读目录