Python线性时间排序——桶排序、基数排序与计数排序

1. 桶排序

1.1 范围为1-M的桶排序

如果有一个数组A，包含N个整数，值从1到M，我们可以得到一种非常快速的排序，桶排序（bucket sort）。留置一个数组S，里面含有M个桶，初始化为0。然后遍历数组A，读入A_i时，S[A_i]增一。所有输入被读进后，扫描数组S得出排好序的表。该算法时间花费O(M+N)，空间上不能原地排序。

初始化序列S

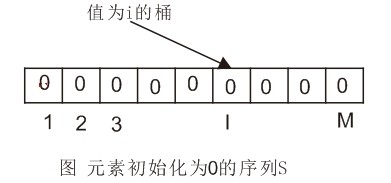
遍历A修改序列S的项

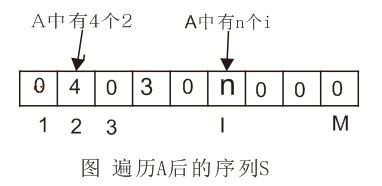
举个例子，排序一个数组[5,3,6,1,2,7,5,10]

值都在1-10之间，建立10个桶：

[0 0 0 0 0 0 0 0 0 0] 桶

[1 2 3 4 5 6 7 8 9 10] 桶代表的值

遍历数组，第一个数字5，第五个桶加1

[0 0 0 0 1 0 0 0 0 0]

第二个数字3，第三个桶加1

[0 0 1 0 1 0 0 0 0 0]

遍历后

[1 1 1 0 2 1 1 0 0 1]

输出

[1 2 3 5 5 6 7 10]

代码

import random

class bucketSort(object):

    def _max(self,oldlist):

        _max=oldlist[0]

        for i in oldlist:

            if i>_max:

                _max=i

        return _max

    def _min(self,oldlist):

        _min=oldlist[0]

        for i in oldlist:

            if i<_min:

                _min=i

        return _min

    def sort(self,oldlist):

        _max=self._max(oldlist)

        _min=self._min(oldlist)

        s=[0 for i in xrange(_min,_max+1)]

        for i in oldlist:

            s[i-_min]+=1

        current=_min

        n=0

        for i in s:

            while i>0:

                oldlist[n]=current

                i-=1

                n+=1

            current+=1

    def __call__(self,oldlist):

        self.sort(oldlist)

        return oldlist

if __name__=='__main__':

    a=[random.randint(0,100) for i in xrange(10)]

    bucketSort()(a)

    print a

1.2 区间[0,1)均匀分布的桶排序

当输入符合均匀分布时，例如，元素均匀的分布在区间[0,1)上，可以将桶排序与其它排序方法结合使用。

如果序列的大小为n，就将[0,1)划分成n个相同大小的子区间(桶),然后将n个输入数分布到各个桶中。先对各个桶中的数进行排序，然后按照次序把各桶中的元素列出来即可。

《算法导论》的描述图：

代码：

class bucketSort(object):

    def insertSort(self,a):

        n=len(a)

        if n<=1:

            pass

        for i in range(1,n):

            key=a[i]

            j=i-1

            while key<a[j] and j>=0:

                a[j+1]=a[j]

                j-=1

            a[j+1]=key

    def sort(self,a):

        n=len(a)

        s=[[] for i in xrange(n)]

        for i in a:

            s[int(i*n)].append(i)

        for i in s:

            self.insertSort(i)

        return [i for j in s for i in j]

    def __call__(self,a):

        return self.sort(a)

if __name__=='__main__':

    from random import random

    from timeit import Timer

    a=[random() for i in xrange(10000)]

    def test_bucket_sort():

        bucketSort()(a)

    def test_builtin_sort():

        sorted(a)

    tests=[test_bucket_sort,test_builtin_sort]

    for test in tests:

        name=test.__name__

        t=Timer(name+'()','from __main__ import '+name)

        print t.timeit(1)

2. 基数排序

基数排序一般用于长度相同的元素组成的数组。首先按照最低有效数字进行排序，然后由低位向高位进行。

329 720 720 329

457 355 329 355

657 436 436 436

839＝＝＝＝≯ 457＝＝＝＝≯ 839＝＝＝＝≯ 457

436 657 355 657

720 329 457 720

355 839 657 839

基数排序可以看做是进行多趟桶排序。每个有效数字都在0-9之间，很适合桶排序，建10个桶很方便。

排序数组 64,8,216，512,27,729,0,1,343,125

第一趟排序：

0 1 512 343 64 125 216 27 8 729

0 1 2 3 4 5 6 7 8 9

第二趟排序：

8 729

1 216 27

0 512 125 343 64

0 1 2 3 4 5 6 7 8 9

第三趟排序：

0 125 216 343 512 729

0 1 2 3 4 5 6 7 8 9

输出：1 8 27 64 125 216 343 512 729

代码：

import random

def radixSort():

    A=[random.randint(1,9999) for i in xrange(10000)]

    for k in xrange(4):  #4轮排序

        s=[[] for i in xrange(10)]

        for i in A:

            s[i/(10**k)%10].append(i)

        A=[a for b in s for a in b]

    return A

　1.3 计数排序

假设n个输入元素中每一个都是介于0到k之间的整数，此处k为某个整数。当k=O(n)时，计数排序的运行时间为Θ(n)。

对每一个数的元素x，确定出小于x的元素个数。有了这一信息就可以把x直接放到最终输出数组中的位置上。

def countingSort(alist,k):

    n=len(alist)

    b=[0 for i in xrange(n)]

    c=[0 for i in xrange(k+1)]

    for i in alist:

        c[i]+=1

    for i in xrange(1,len(c)):

        c[i]=c[i-1]+c[i]

    for i in alist:

        b[c[i]-1]=i

        c[i]-=1

    return b

if __name__=='__main__':

    a=[random.randint(0,100) for i in xrange(100)]

    print countingSort(a,100)