2012 Asia Hangzhou Regional Contest

Friend Chains http://acm.hdu.edu.cn/showproblem.php?pid=4460

图的最远两点距离，任意选个点bfs，如果有不能到的点直接-1.然后对于所有距离最远的点都bfs一次。最坏n^2

邻接表

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<queue>
 #include<map>
 #define mt(a,b) memset(a,b,sizeof(a))
 using namespace std;
 const int M=;
 char a[],b[];
 map<string,int> name;
 struct G{
     struct E{
         int v,next;
     }e[M*];
     int le,head[M];
     void init(){
         le=;
         mt(head,-);
     }
     void add(int u,int v){
         e[le].v=v;
         e[le].next=head[u];
         head[u]=le++;
     }
 }g;
 int dist[M],id[M];
 bool vis[M];
 queue<int> q;
 void bfs(int s){
     mt(vis,);
     mt(dist,-);
     vis[s]=true;
     dist[s]=;
     while(!q.empty()) q.pop();
     q.push(s);
     while(!q.empty()){
         int u=q.front();
         q.pop();
         for(int i=g.head[u];~i;i=g.e[i].next){
             int v=g.e[i].v;
             if(!vis[v]){
                 vis[v]=true;
                 dist[v]=dist[u]+;
                 q.push(v);
             }
         }
     }
 }
 int main(){
     int n,m;
     while(~scanf("%d",&n),n){
         name.clear();
         for(int i=;i<n;i++){
             scanf("%s",a);
             name[(string)a]=i;
         }
         scanf("%d",&m);
         g.init();
         while(m--){
             scanf("%s%s",a,b);
             int u=name[(string)a];
             int v=name[(string)b];
             g.add(u,v);
             g.add(v,u);
         }
         bfs();
         bool flag=false;
         for(int i=;i<n;i++){
             if(dist[i]==-){
                 flag=true;
                 break;
             }
         }
         if(flag){
             puts("-1");
             continue;
         }
         int big=;
         for(int i=;i<n;i++){
             big=max(big,dist[i]);
         }
         int ld=;
         for(int i=;i<n;i++){
             if(dist[i]==big){
                 id[ld++]=i;
             }
         }
         int ans=;
         for(int i=;i<ld;i++){
             bfs(id[i]);
             for(int j=;j<n;j++){
                 ans=max(ans,dist[j]);
             }
         }
         printf("%d\n",ans);
     }
     return ;
 }

vector竟然还快些

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<queue>
 #include<map>
 #define mt(a,b) memset(a,b,sizeof(a))
 using namespace std;
 const int M=;
 char a[],b[];
 map<string,int> name;
 vector<int> g[M];
 int dist[M],id[M];
 bool vis[M];
 queue<int> q;
 void bfs(int s){
     mt(vis,);
     mt(dist,-);
     vis[s]=true;
     dist[s]=;
     while(!q.empty()) q.pop();
     q.push(s);
     while(!q.empty()){
         int u=q.front();
         q.pop();
         int len=g[u].size();
         for(int i=;i<len;i++){
             int v=g[u][i];
             if(!vis[v]){
                 vis[v]=true;
                 dist[v]=dist[u]+;
                 q.push(v);
             }
         }
     }
 }
 int main(){
     int n,m;
     while(~scanf("%d",&n),n){
         name.clear();
         for(int i=;i<n;i++){
             scanf("%s",a);
             name[(string)a]=i;
             g[i].clear();
         }
         scanf("%d",&m);
         while(m--){
             scanf("%s%s",a,b);
             int u=name[(string)a];
             int v=name[(string)b];
             g[u].push_back(v);
             g[v].push_back(u);
         }
         bfs();
         bool flag=false;
         for(int i=;i<n;i++){
             if(dist[i]==-){
                 flag=true;
                 break;
             }
         }
         if(flag){
             puts("-1");
             continue;
         }
         int big=;
         for(int i=;i<n;i++){
             big=max(big,dist[i]);
         }
         int ld=;
         for(int i=;i<n;i++){
             if(dist[i]==big){
                 id[ld++]=i;
             }
         }
         int ans=;
         for(int i=;i<ld;i++){
             bfs(id[i]);
             for(int j=;j<n;j++){
                 ans=max(ans,dist[j]);
             }
         }
         printf("%d\n",ans);
     }
     return ;
 }

The Power of Xiangqi http://acm.hdu.edu.cn/showproblem.php?pid=4461

o（n）水题。每个旗子有权值，算一算权值比一比。注意至少1分。如果b和c有一个没有就扣一分。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define mt(a,b) memset(a,b,sizeof(a))
 using namespace std;
 const int M=;
 int sa[M],sb[M];
 int val[]={,,,,,,};
 int main(){
     int t,n;
     char op[];
     while(~scanf("%d",&t)){
         while(t--){
             mt(sa,);
             mt(sb,);
             scanf("%d",&n);
             while(n--){
                 scanf("%s",op);
                 sa[op[]-'A']++;
             }
             scanf("%d",&n);
             while(n--){
                 scanf("%s",op);
                 sb[op[]-'A']++;
             }
             int suma=,sumb=;
             for(int i=;i<;i++){
                 suma+=val[i]*sa[i];
                 sumb+=val[i]*sb[i];
             }
             if(!sa[]||!sa[]) suma--;
             if(!sb[]||!sb[]) sumb--;
             suma=max(,suma);
             sumb=max(,sumb);
             if(suma>sumb){
                 puts("red");
             }
             else if(suma<sumb){
                 puts("black");
             }
             else{
                 puts("tie");
             }
         }
     }
     return ;
 }

Scaring the Birds http://acm.hdu.edu.cn/showproblem.php?pid=4462

二进制枚举放的情况，判断能否覆盖所有的玉米，注意能放的地方已经没有玉米了，不用判这个点。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define mt(a,b) memset(a,b,sizeof(a))
 using namespace std;
 const int inf=0x3f3f3f3f;
 const int M=;
 bool mat[M][M];
 struct G{
     int x,y,r;
 }p[];
 int one(int x){
     int res=;
     while(x){
         if(x&) res++;
         x>>=;
     }
     return res;
 }
 int used[];
 int main(){
     int n,m;
     while(~scanf("%d",&n),n){
         scanf("%d",&m);
         mt(mat,);
         for(int i=;i<m;i++){
             scanf("%d%d",&p[i].x,&p[i].y);
             mat[p[i].x][p[i].y]=true;
         }
         for(int i=;i<m;i++){
             scanf("%d",&p[i].r);
         }
         int all=<<m;
         int ans=inf;
         for(int i=;i<all;i++){
             int now=one(i);
             if(now>=ans) continue;
             int lu=;
             for(int j=;j<m;j++){
                 if((i>>j)&){
                     used[lu++]=j;
                 }
             }
             bool flag=true;
             for(int x=;x<=n;x++){
                 for(int y=;y<=n;y++){
                     if(mat[x][y]) continue;
                     bool ok=false;
                     for(int j=;j<lu;j++){
                         int id=used[j];
                         if(abs(x-p[id].x)+abs(y-p[id].y)<=p[id].r){
                             ok=true;
                             break;
                         }
                     }
                     if(!ok){
                         flag=false;
                         break;
                     }
                 }
                 if(!flag) break;
             }
             if(flag){
                 ans=min(ans,now);
             }
         }
         if(ans==inf) ans=-;
         printf("%d\n",ans);
     }
     return ;
 }

Outlets http://acm.hdu.edu.cn/showproblem.php?pid=4463

最小生成树，必须有一条边先加进去，那就加个权值为零的，然后ans直接加上边权，这样就保证一定有这个边了。

 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #define mt(a,b) memset(a,b,sizeof(a))
 using namespace std;
 const int M=;
 class Kruskal { ///最小生成树(无向图)o(ME*logME)
     typedef double typec;///边权的类型
     static const int ME=M*M;///边的个数
     static const int MV=M;///点的个数
     class UnionFindSet { ///并查集
         int par[MV];
     public:
         void init() {
             mt(par,-);
         }
         int getroot(int x) {
             int i=x,j=x,temp;
             while(par[i]>=) i=par[i];
             while(j!=i) {
                 temp=par[j];
                 par[j]=i;
                 j=temp;
             }
             return i;
         }
         bool unite(int x,int y) {
             int p=getroot(x);
             int q=getroot(y);
             if(p==q)return false;
             if(par[p]>par[q]) {
                 par[q]+=par[p];
                 par[p]=q;
             } else {
                 par[p]+=par[q];
                 par[q]=p;
             }
             return true;
         }
     } f;
     struct E {
         int u,v;
         typec w;
         friend bool operator < (E a,E b) {
             return a.w<b.w;
         }
     } e[ME];
     int le,num,n;
     typec res;
 public:
     void init(int tn){///传入点的个数
         n=tn;
         le=res=;
         f.init();
         num=;
     }
     void add(int u,int v,typec w) {
         e[le].u=u;
         e[le].v=v;
         e[le].w=w;
         le++;
     }
     typec solve(){///返回-1不连通
         sort(e,e+le);
         for(int i=; i<le&&num<n; i++) {
             if(f.unite(e[i].u,e[i].v)) {
                 num++;
                 res+=e[i].w;
             }
         }
         if(num<n) res=-;
         return res;
     }
 }gx;
 struct point{
     double x,y;
 }p[M];
 double Distance(point p1,point p2) {
     return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
 }
 int main(){
     int n,x,y;
     while(~scanf("%d",&n),n){
         scanf("%d%d",&x,&y);
         for(int i=;i<n;i++){
             scanf("%lf%lf",&p[i].x,&p[i].y);
         }
         gx.init(n);
         x--;
         y--;
         if(x>y) swap(x,y);
         for(int i=;i<n;i++){
             for(int j=i+;j<n;j++){
                 if(i==x&&j==y){
                     gx.add(i,j,);
                 }
                 else{
                     gx.add(i,j,Distance(p[i],p[j]));
                 }
             }
         }
         double ans=Distance(p[x],p[y]);
         ans+=gx.solve();
         printf("%.2f\n",ans);
     }
     return ;
 }

Stealing a Cake http://acm.hdu.edu.cn/showproblem.php?pid=4454

从起点走到圆上任意一点，然后从那个点走到矩形上任意一点。求总的路程最小。

考虑起点到圆，只可能走两个切线之间，所以就有一个角度的限制，可以枚举这个角度，然后求出和圆的交点，然后再用这个交点求出到矩形最近距离，所有情况取个最小值。

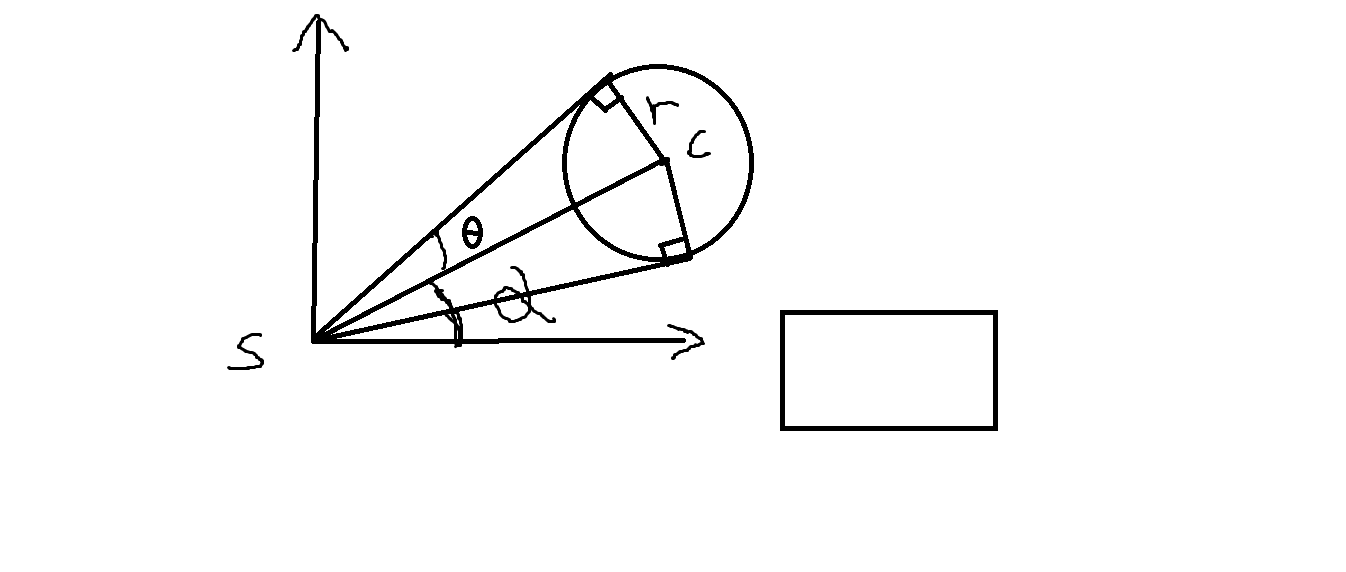
设起点到圆心的直线sc与坐标轴夹角α。设sc与切线夹角θ 。则我们只要枚举0到θ，就能算出一个交点，注意，要取靠近s的交点。然后通过交点可以算出关于se直线的对称点。这样便枚举了所有可能的点的走法。

当前枚举到的直线斜率是 tan（θ+α） 又知道s经过这个直线，所以就可以算出直线上任意一点。然后就算直线和圆的交点，然后取近的交点，分别和矩形四个边算距离，也是取最小。对称点也同理可得。

 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 const double eps=1e-;
 const double pi=acos(-1.0);
 const int inf=0x3f3f3f3f;
 struct point {
     double x,y;
 } s,c,p[]; ///起点，圆心，矩形
 double Distance(point p1,point p2) {
     return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
 }
 point intersection(point u1,point u2,point v1,point v2) {
     point ret=u1;
     double t=((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x)) /((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x));
     ret.x+=(u2.x-u1.x)*t;
     ret.y+=(u2.y-u1.y)*t;
     return ret;
 }
 void intersection_line_circle(point c,double r,point l1,point l2,point& p1,point& p2) {
     point p=c;
     double t;
     p.x+=l1.y-l2.y;
     p.y+=l2.x-l1.x;
     p=intersection(p,c,l1,l2);
     t=sqrt(r*r-Distance(p,c)*Distance(p,c))/Distance(l1,l2);
     p1.x=p.x+(l2.x-l1.x)*t;
     p1.y=p.y+(l2.y-l1.y)*t;
     p2.x=p.x-(l2.x-l1.x)*t;
     p2.y=p.y-(l2.y-l1.y)*t;
 }
 double xmult(point p1,point p2,point p0) {
     return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
 }
 double disptoseg(point p,point l1,point l2) {
     point t=p;
     t.x+=l1.y-l2.y,t.y+=l2.x-l1.x;
     if (xmult(l1,t,p)*xmult(l2,t,p)>eps) return Distance(p,l1)<Distance(p,l2)?Distance(p,l1):Distance(p,l2);
     return fabs(xmult(p,l1,l2))/Distance(l1,l2);
 }
 point ptoseg(point p,point l1,point l2) {
     point t=p;
     t.x+=l1.y-l2.y,t.y+=l2.x-l1.x;
     if (xmult(l1,t,p)*xmult(l2,t,p)>eps) return Distance(p,l1)<Distance(p,l2)?l1:l2;
     return intersection(p,t,l1,l2);
 }
 double jiaotoju(point pp) {
     double res=inf;
     for(int i=; i<; i++) {
         res=min(res,disptoseg(pp,p[i],p[i+]));
     }
     return res;
 }
 int main() {
     double r,x1,x2,y1,y2;
     while(~scanf("%lf%lf",&s.x,&s.y),s.x!=||s.y!=) {
         scanf("%lf%lf%lf",&c.x,&c.y,&r);
         scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
         if(x1>x2) swap(x1,x2);
         if(y1>y2) swap(y1,y2);
         p[].x=x1;
         p[].y=y1;
         p[].x=x2;
         p[].y=y1;
         p[].x=x2;
         p[].y=y2;
         p[].x=x1;
         p[].y=y2;
         p[]=p[];
         double afa,tanafa;///起点到圆心的直线与x轴夹角，就是直线斜率
         if(fabs(s.x-c.x)<eps) {
             afa=*pi/;
         } else {
             tanafa=(s.y-c.y)/(s.x-c.x);
             afa=atan(tanafa);
         }
         double xita,sinxita;///起点到圆心的直线与切线夹角
         sinxita=r/Distance(s,c);
         xita=asin(sinxita);
         double bigxita=xita;
         double add=bigxita/;
         double delx,dely,dist1,dist2;
         point L2,J1,J2,center;
         double ans=inf,sum;
         for(double x=; x<=bigxita; x+=add) {
             xita=x+afa;
             delx=;
             dely=tan(xita)*delx;
             L2.x=s.x+delx;
             L2.y=s.y+dely;
             intersection_line_circle(c,r,s,L2,J1,J2);
             dist1=Distance(s,J1);
             dist2=Distance(s,J2);
             if(dist1>dist2) {
                 swap(dist1,dist2);
                 swap(J1,J2);
             }
             ans=min(ans,dist1+jiaotoju(J1));
             center=ptoseg(J1,s,c);
             J2.x=*center.x-J1.x;
             J2.y=*center.y-J1.y;
             ans=min(ans,dist1+jiaotoju(J2));
         }
         printf("%.2f\n",ans);
     }
     return ;
 }

事实上从上面的枚举可以看出，正解只有一个，并且一定在α-θ到α+θ之间。并且偏离正解越远，肯定距离越长，那么就是一个开口向上的二次函数，就可以对这个区间三分查找。

 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 const double eps=1e-;
 const double pi=acos(-1.0);
 const int inf=0x3f3f3f3f;
 struct point {
     double x,y;
 } s,c,p[]; ///起点，圆心，矩形
 double Distance(point p1,point p2) {
     return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
 }
 point intersection(point u1,point u2,point v1,point v2) {
     point ret=u1;
     double t=((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x)) /((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x));
     ret.x+=(u2.x-u1.x)*t;
     ret.y+=(u2.y-u1.y)*t;
     return ret;
 }
 void intersection_line_circle(point c,double r,point l1,point l2,point& p1,point& p2) {
     point p=c;
     double t;
     p.x+=l1.y-l2.y;
     p.y+=l2.x-l1.x;
     p=intersection(p,c,l1,l2);
     t=sqrt(r*r-Distance(p,c)*Distance(p,c))/Distance(l1,l2);
     p1.x=p.x+(l2.x-l1.x)*t;
     p1.y=p.y+(l2.y-l1.y)*t;
     p2.x=p.x-(l2.x-l1.x)*t;
     p2.y=p.y-(l2.y-l1.y)*t;
 }
 double xmult(point p1,point p2,point p0) {
     return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
 }
 double disptoseg(point p,point l1,point l2) {
     point t=p;
     t.x+=l1.y-l2.y,t.y+=l2.x-l1.x;
     if (xmult(l1,t,p)*xmult(l2,t,p)>eps) return Distance(p,l1)<Distance(p,l2)?Distance(p,l1):Distance(p,l2);
     return fabs(xmult(p,l1,l2))/Distance(l1,l2);
 }
 point ptoseg(point p,point l1,point l2) {
     point t=p;
     t.x+=l1.y-l2.y,t.y+=l2.x-l1.x;
     if (xmult(l1,t,p)*xmult(l2,t,p)>eps) return Distance(p,l1)<Distance(p,l2)?l1:l2;
     return intersection(p,t,l1,l2);
 }
 double jiaotoju(point pp) {
     double res=inf;
     for(int i=; i<; i++) {
         res=min(res,disptoseg(pp,p[i],p[i+]));
     }
     return res;
 }
 double r;
 double f(double xita) {
     double delx,dely,dist1,dist2;
     point L2,J1,J2,center;
     delx=;
     dely=tan(xita)*delx;
     L2.x=s.x+delx;
     L2.y=s.y+dely;
     intersection_line_circle(c,r,s,L2,J1,J2);
     dist1=Distance(s,J1);
     dist2=Distance(s,J2);
     if(dist1>dist2) {
         swap(dist1,dist2);
         swap(J1,J2);
     }
     double res=dist1+jiaotoju(J1);
     center=ptoseg(J1,s,c);
     J2.x=*center.x-J1.x;
     J2.y=*center.y-J1.y;
     res=min(res,dist1+jiaotoju(J2));
     return res;
 }
 double TernarySearch(double L,double R) { /// 三分查找
     while(R-L>eps) {
         double LL=(L*+R)/;
         double RR=(L+R*)/;
         if(f(LL)<f(RR))  ///f为对应的值  这里求最小值
             R=RR;
         else
             L=LL;
     }
     return L;
 }
 int main() {
     double x1,x2,y1,y2;
     while(~scanf("%lf%lf",&s.x,&s.y),s.x!=||s.y!=) {
         scanf("%lf%lf%lf",&c.x,&c.y,&r);
         scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
         if(x1>x2) swap(x1,x2);
         if(y1>y2) swap(y1,y2);
         p[].x=x1;
         p[].y=y1;
         p[].x=x2;
         p[].y=y1;
         p[].x=x2;
         p[].y=y2;
         p[].x=x1;
         p[].y=y2;
         p[]=p[];
         double afa,tanafa;///起点到圆心的直线与x轴夹角，就是直线斜率
         if(fabs(s.x-c.x)<eps) {
             afa=*pi/;
         } else {
             tanafa=(s.y-c.y)/(s.x-c.x);
             afa=atan(tanafa);
         }
         double xita,sinxita;///起点到圆心的直线与切线夹角
         sinxita=r/Distance(s,c);
         xita=asin(sinxita);
         double ans=TernarySearch(afa-xita,afa+xita);
         printf("%.2f\n",f(ans));
     }
     return ;
 }

Shoot the Airplane http://acm.hdu.edu.cn/showproblem.php?pid=4458

题意：子弹竖直上抛运动，多边形水平匀速运动。问是否能有一个时间点使得子弹在多边形内。

暴力枚举时间，有了时间就知道子弹的位置和多边形的位置，然后判断点在多边形内就行。注意边上的不算。

 #include<cstdio>
 #include<cstdlib>
 const double eps=1e-;
 struct point{
     double x,y;
 }p[],now[],s;
 class PolygonJudge { //任意多边形判定
 #define zero(x) (((x)>0?(x):-(x))<eps)
     double xmult(point p1,point p2,point p0) {
         return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
     }
 public:
     int inside_polygon(point q,int n,point p[],int on_edge=) {//判点在任意多边形内,顶点按顺时针或逆时针给出
         point q2;
         const int offset=;//on_edge表示点在多边形边上时的返回值,offset为多边形坐标上限
         int i=,cnt;
         while (i<n)
             for (cnt=i=,q2.x=rand()+offset,q2.y=rand()+offset; i<n; i++)
                 if(zero(xmult(q,p[i],p[(i+)%n]))&&(p[i].x-q.x)*(p[(i+)%n].x-q.x)<eps&&(p[i].y-q.y)*(p[(i+)%n].y-q.y)<eps)
                     return on_edge;
                 else if (zero(xmult(q,q2,p[i])))
                     break;
                 else if (xmult(q,p[i],q2)*xmult(q,p[(i+)%n],q2)<-eps&&xmult(p[i],q,p[(i+)%n])*xmult(p[i],q2,p[(i+)%n])<-eps)
                     cnt++;
         return cnt&;
     }
 } gx;
 int main(){
     int v,b,g,n;
     while(~scanf("%d%d%d",&v,&b,&g),v|b|g){
         scanf("%d",&n);
         for(int i=;i<n;i++){
             scanf("%lf%lf",&p[i].x,&p[i].y);
         }
         double bigt;
         if(g){
             bigt=2.0*b/g;
         }
         else{
             bigt=120.0/b;
         }
         double add=bigt/;
         bool flag=false;
         double ans;
         for(double t=;t<=bigt;t+=add){
             s.x=;
             s.y=b*t-0.5*g*t*t;
             for(int i=;i<n;i++){
                 now[i]=p[i];
                 now[i].x+=v*t;
             }
             if(gx.inside_polygon(s,n,now,)){
                 flag=true;
                 ans=t;
                 break;
             }
         }
         if(!flag) puts("Miss!");
         else{
             printf("%.2f\n",ans);
         }
     }
     return ;
 }

还有一种解法，相对运动的思想，多边形向左运动，相当于多边形不动，子弹向右有一样的速度，那么子弹就是个抛物线，求抛物线是否进入多边形内。至今没敲出来，先放一放。

end