OpenCV码源笔记——RandomTrees (二)(Forest)

源码细节：

● 训练函数

bool CvRTrees::train( const CvMat* _train_data, int _tflag,
                        const CvMat* _responses, const CvMat* _var_idx,
                        const CvMat* _sample_idx, const CvMat* _var_type,
                        const CvMat* _missing_mask, CvRTParams params )

Step1：清理现场，调用clear()函数，删除和释放所有决策树，清除训练数据等；

Step2：构造适用于单棵决策树训练的参数包CvDTreeParams，主要就是对CvRTParams中一些参数的拷贝；

Step3：构建训练数据CvDTreeTrainData，主要涉及CvDTreeTrainData::set_data()函数。CvDTreeTrainData包含CvDTreeParams格式的参数包、被所有树共享的训练数据（优化结构使最优分裂更迅速）以及response类型和类数目等常用数据，还包括最终构造出来的树节点缓存等。

Step4：检查CvRTParams::nactive_vars使其不大于最大启用变量数；若nactive_vars传参为0，则默认赋值为最大启用变量数的平方根；若小于0，则报错退出；

Step5：创建并初始化一个变量活跃Mask（1×变量总数），初始化过程设置前nactive_vars个变量mask为1（活跃），其余为0（非活跃）；

Step6：调用CvRTrees::grow_forest()开始生成森林。

● 生成森林

bool CvRTrees::grow_forest( const CvTermCriteria term_crit )

Step1：如果需要以准确率为终止条件或者需要计算变量的重要值（is_oob_or_vimportance = true），则需要创建并初始化以下数据：
oob_sample_votes  用于分类问题，样本数量×类数量，存储每个样本的测试分类；
oob_responses  用于回归问题，2×样本数量，这是一个不直接使用的数据，旨在为以下两个数据开辟空间；
oob_predictions_sum  用于回归问题，1×样本数量，存储每个样本的预测值之和；
oob_num_of_predictions  用于回归问题，1×样本数量，存储每个样本被预测的次数；
oob_samples_perm_ptr  用于存储乱序样本，样本数量×类数量；
samples_ptr / missing_ptr / true_resp_ptr  从训练数据中拷贝的样本数组、缺失Mask和真实response数组；
maximal_response  response的最大绝对值。

Step2：初始化以下数据：
trees  CvForestTree格式的单棵树集合，共max_ntrees棵，max_ntrees由CvDTreeParams定义；
sample_idx_mask_for_tree  存储每个样本是否参与当前树的构建，1×样本数量；
sample_idx_for_tree  存储在构建当前树时参与的样本序号，1×样本数量；

Step3：随机生成参与当前树构建的样本集（sample_idx_for_tree定义），调用CvForestTree::train()函数生成当前树，加入树集合中。CvForestTree::train()先调用CvDTreeTrainData::subsample_data()函数整理样本集，再通过调用CvForestTree::try_split_node()完成树的生成，try_split_node是一个递归函数，在分割当前节点后，会调用分割左右节点的try_split_node函数，直到准确率达到标准或者节点样本数过少；

Step4：如果需要以准确率为终止条件或者需要计算变量的重要值（is_oob_or_vimportance = true），则：
使用未参与当前树构建的样本，测试当前树的预测准确率；
若需计算变量的重要值，对于每一种变量，对每一个非参与样本，替换其该位置的变量值为另一随机样本的该变量值，再进行预测，其正确率的统计值与上一步当前树的预测准确率的差，将会累计到该变量的重要值中；

Step5：重复Step3 – 4，直到终止条件；

Step6：若需计算变量的重要值，归一化变量重要性到[0, 1]。

●训练单棵树

void CvDTree::try_split_node( CvDTreeNode* node )

Step1：调用CvDtree::calc_node_value()函数：对于分类问题，计算当前节点样本中最大样本数量的类别，最为该节点的类别，同时计算更新交叉验证错误率（命名带有cv_的数据）；对于回归问题，也是类似的计算当前节点样本值的均值作为该节点的值，也计算更新交叉验证错误率；

Step2：作终止条件判断：样本数量是否过少；深度是否大于最大指定深度；对于分类问题，该节点是否只有一种类别；对于回归问题，交叉验证错误率是否已达到指定精度要求。若是，则停止分裂；

Step3：若可分裂，调用CvForestTree::find_best_split()函数寻找最优分裂，首先随机当前节点的活跃变量，再使用ForestTreeBestSplitFinder完成：ForestTreeBestSplitFinder对分类或回归问题、变量是否可数，分别处理。对于每个可用变量调用相应的find函数，获得针对某一变量的最佳分裂，再在这所有最佳分裂中依照quality值寻找最最优。find函数只关描述分类问题（回归其实差不多）：

CvForestTree::find_split_ord_class()：可数变量，在搜寻开始前，最主要的工作是建立一个按变量值升序的样本index序列，搜寻按照这个序列进行。最优分裂的依据是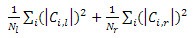

也就是左右分裂所有类别中样本数量的平方  / 左右分裂的样本总数，再相加（= =还是公式看的懂些吧。。）
比如说，排序后的 A A B A B B C B C C 这样的序列，比较这样两种分裂方法：
          A A B A B B | C B C C 和 A A B A B B C B | C C
          第一种的quality是 (3² + 3² + 0²) / 6 + (0² + 1² + 3²) / 4 = 5.5
          第二种的quality是 (3² + 4² + 1²) / 8 + (0² + 0² + 2²) / 2 = 5.25
第一种更优秀些。感性地看，第一种的左分裂只有AB，右分裂只有BC，那么可能再来一次分裂就能完全分辨；而第二种虽然右分裂只有C，但是左分裂一团糟，其实完全没做什么事情。
最优搜寻过程中会跳过一些相差很小的以及不活跃的变量值，主要是为了避免在连续变量取值段出现分裂，这在真实预测中会降低树的鲁棒性。

CvForestTree::find_split_cat_class()：不可数变量，分裂quality的计算与可数情况相似，不同的是分类的标准，不再是阈值对数值的左右划分，而是对变量取值的子集划分，比如将a b c d e五种可取变量值分为{a} + {b, c, d, e}、{a, b} + {c, d, e}等多种形式比较quality。统计的是左右分裂每个类别取该分裂子集中的变量值的样本数量的平方 / 左右分裂的样本总数，再相加。同样，搜寻会跳过样本数量很少的以及不活跃的分类取值。

Step4：若不存在最优分裂或者无法分裂，则释放相关数据后返回；否则，处理代理分裂、分割左右分裂数据、调用左右后续分裂。

---

References：
[1] OpenCV 2.3 Online Documentation: http://opencv.itseez.com/modules/ml/doc/random_trees.html
[2] Random Forests, Leo Breiman and Adele Cutler: http://www.stat.berkeley.edu/users/breiman/RandomForests/cc_home.htm
[3] T. Hastie, R. Tibshirani, J. H. Friedman. The Elements of Statistical Learning. ISBN-13 978-0387952840, 2003, Springer.

转自：http://lincccc.com/?p=46

from: http://blog.csdn.net/yangtrees/article/details/7488913