机器学习第三课（EM算法和高斯混合模型）

极大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。最大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

     我们先来假设这样一个问题：要求解人群（100人）中男女身高的分布，这里很明显有两种分布，男和女，但是事先我们并不知道他们服从哪种分布，而且我们也不知道男的有多少人，女的有多少人，那么怎么办呢？如果我们用混合高斯模型，我们假设男和女的分布都是符合高斯分布的，然后给定这个高斯分布一个初始值，这样这个高斯分布就是已知的了。接着，用这个已经的高斯分布来估计男的多少人，女的多少人，假设男和女的类别分布为Q(z)，这样我们就可以求Q(z)的期望了，用期望来表示下一次迭代类别的初始值，这样我们就知道男和女的所属类别了，我们就可以用最大似然函数来估新的高斯模型的参数了。重复上述步骤…直到收敛！

    ps：极大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。最大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

   EM算法，这是cv界比较有名的一种算法了，虽然很早就听说过，但真正深究还是最近几天看斯坦福公开课笔记的时候。之所以EM和MoG放在一起，是因为我们在求解MoG模型的时候需要用到EM算法，所以这里我们先来介绍下EM算法。

    在介绍EM算法的之前，我们先来普及下Jensen不等式的知识。首先我们来给出Jensen不等式的定义：

                                                 

    定理很简单，总结下来就是这么几点。如果f是一个凸函数并且二阶导数大于零（上文中有提出），则有。进一步， 若二阶导数恒大于 0，则不等式等号成立当且仅当 x=E[x]，即 x 是固定值。若二阶导数的不等号方向逆转，则不等式的不等号方向逆转。如下图：

                                                                    

    好了，知道了Jensen不等式，我们下面来探讨EM算法的一般形式。

    suppose we have a training set  consist of  m independent examples，假设样本的类别z服从某种未知的分布，那么对于这种隐含变量的模型我们可以求出它的似然函数为（求似然函数是为了求解我们假设模型中的各个参数，我们在求解一个分类或者回归问题时，通常需要选定一个模型，比如NB，GDA，logistic regression，然后利用最大似然求解模型的参数）：

                                                                          

    这里我们并不知道所服从的分布，只知道它们服从某种概率分布就足够了。接下来我们需要求解参数来使得以上的最大即可，由于中对数函数相加的情况使得求解非常困难。于是我们转化为下面这样处理：

                                                                     

    式中我们引入了z的一种未知分布(怎么选择下面会讲)， 即，继续推导我们有

                                                                     

    上式中我们用到了Jensen不等式，由于log函数式一个凹函数，所以不等式的不等号要逆转了。简而言之就是：

                                                                    

    也就是说有一个下界，而这个下界中的对数已经放在了求和里面，因而求偏导比较容易。那么我们可不可以把minimum 转化为minimum lowbound呢。有了这个思想之后我们只需要证明即可。假设当前的参数为，在下界上计算出极大似人函数的新的参数为，如果能够保证，我们就只需要在下界上进行极大似然估计就行了。证明如下：

                                                                    

    这个式子前面几项不难理解，关键是最后的一个等式，怎么才能保证呢？ 哈哈，还记得Jensen不等式里面等式成立的条件么，对的，就是这个x=E[x]，对应EM算法中就是要使

                                                                                    

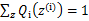    再加上条件，对此式子做进一步推导，我们知道，那么也就有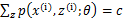,我们就可以这样选择Q(Z):

                                                                       

    这样我们就可以选出对Z的概率估计Q了。于是我们就得到了EM算法的一半不周，如下：

                                                                       

     为了便于理解，这里画一幅图来加深大家的印象

                                                                    

    到此为此我们就用一个下界lowbound，通过在lowbound上求解最大似然函数，从而不断更新参数，最终解决EM算法的参数求解问题。

 

    Mixtures of Gaussians（GDA）

    混合高斯分布(MoG)也是一种无监督学习算法，常用于聚类。当聚类问题中各个类别的尺寸不同、聚类间有相关关系的时候，往往使用 MoG 更合适。对一个样本来说， MoG 得到的是其属于各个类的概率(通过计算后验概率得到)，而不是完全的属于某个类，这种聚类方法被成为软聚类。一般说来， 任意形状的概率分布都可以用多个高斯分布函数去近似，因而，MoG 的应用也比较广泛。

    先来举一个例子帮助大家理解，如下图：

                                                                      

    这是一个二维的高斯混合分布，数据点由均值为(-1,-2)和(1,2)的两个高斯分布生成。 根据数据点属于两个高斯分布的后验概率大小对数据点进行分类，可得下图所示的聚类结果：

                                                                       

    在MoG中，由于事先我们不知道数据的分布情况，我们需要先提出两种假设：

    假设 1 ：z 服从多项式分布， 即：

                                                                              

    假设 2： 已知 z 时， x 服从正态分布，即条件概率 p(x|z)服从正态分布，即：

                                                                               

    则 x 与 z 的联合分布概率函数为：

 

                                                                          

    接下来求似然函数

                                                                          

    利用似然函数求解参数的值

                                                                   

    但是现在的问题是，我们的两个假设不一定是成立的，那么如果在事先不知道样本及其所属类别的分布情况是，我们又该怎么来求解各个参数的值呢。想到了没有，刚刚我们讲到的EM算法就是来解决这样一种问题的呀，所以我们想到了她-EM，就是水到渠成的事了。既然EM算法我们已经讲解了，那么现在就直接拿来解MoG就是了，步骤如下：

                                                                    

                                                               

    具体说来，在E-step中， Z的概率更新如下：

                                                                   

    如假设所言，是正态分布，是多项式分布。

    在 M-step中， 根据E-step得到的Z的分布情况，对参数进行重新估计：

                                                                                 

                                                                  

    这样通过不断的迭代，不断的更新参数，我们就可以求解出MoG模型的参数了。从分析过程来看，MoG对不确定分布的样本处理效果会比较好。