P3382 【模板】三分法

题目描述

如题，给出一个N次函数，保证在范围[l,r]内存在一点x，使得[l,x]上单调增，[x,r]上单调减。试求出x的值。

输入输出格式

输入格式：

第一行一次包含一个正整数N和两个实数l、r，含义如题目描述所示。

第二行包含N+1个实数，从高到低依次表示该N次函数各项的系数。

输出格式：

输出为一行，包含一个实数，即为x的值。四舍五入保留5位小数。

输入输出样例

输入样例#1：

3 -0.9981 0.5
1 -3 -3 1

输出样例#1：

-0.41421

说明

时空限制：50ms,128M

数据规模：

对于100%的数据：7<=N<=13

样例说明：

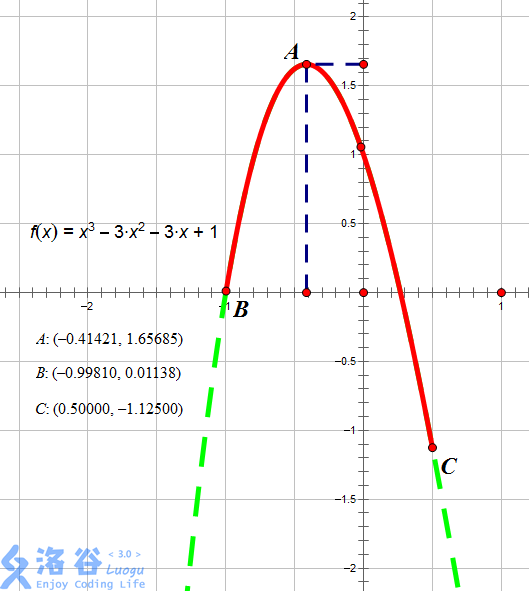
如图所示，红色段即为该函数f(x)=x^3-3x^2-3x+1在区间[-0.9981,0.5]上的图像。

当x=-0.41421时图像位于最高点，故此时函数在[l,x]上单调增，[x,r]上单调减，故x=-0.41421，输出-0.41421。

三分法：(按照题目来)

风格1

#include<cstdio>
#include<cmath>
using namespace std;
const int N=1e5+;
const double eps=1e-;
int n;double L,R,a[N];
double f(double x){
    double res=a[]+a[]*x;
    for(int i=n;i>;i--) res=res+a[i]*pow(x,i);
    return res;
}
double three_divide(){
    double l=L,r=R,lmid,rmid;
    while(r-l>eps){
        lmid=(l+r)/2.0;
        rmid=(r+lmid)/2.0;
        if(f(lmid)<f(rmid)) l=lmid;
        else r=rmid;
    }
    return l;
}
int main(){
    scanf("%d",&n);
    scanf("%lf%lf",&L,&R);
    for(int i=n;i>=;i--) scanf("%lf",&a[i]);
    printf("%.5lf",three_divide());
    return ;
}

风格2

#include<cstdio>
#include<cmath>
using namespace std;
const int N=1e5+;
const double eps=1e-;
int n;double L,R,a[N];
double f(double x){
    double res=a[]+a[]*x;
    for(int i=n;i>;i--) res=res+a[i]*pow(x,i);
    return res;
}
double three_divide(){
    double l=L,r=R,lmid,rmid;
    while(r-l>eps){
        lmid=(*l+r)/3.0;
        rmid=(l+*r)/3.0;
        if(f(lmid)<f(rmid)) l=lmid;
        else r=rmid;
    }
    return l;
}
int main(){
    scanf("%d",&n);
    scanf("%lf%lf",&L,&R);
    for(int i=n;i>=;i--) scanf("%lf",&a[i]);
    printf("%.5lf",three_divide());
    return ;
}

二分法：(用导函数求0点)

#include<cstdio>
#include<cmath>
using namespace std;
const int N=1e5+;
const double eps=1e-;
int n;double L,R,a[N];
double F(double x){
    double res=a[];
    for(int i=n;i>;i--) res=res+(double)i*a[i]*pow(x,i-);
    return res;
}
double two_divide(){
    double l=L,r=R,mid;
    while(r-l>eps){
        mid=(l+r)/2.0;
        if(F(mid)<=) r=mid;
        else l=mid;
    }
    return l;
}
int main(){
    scanf("%d",&n);
    scanf("%lf%lf",&L,&R);
    for(int i=n;i>=;i--) scanf("%lf",&a[i]);
    printf("%.5lf",two_divide());
    return ;
}