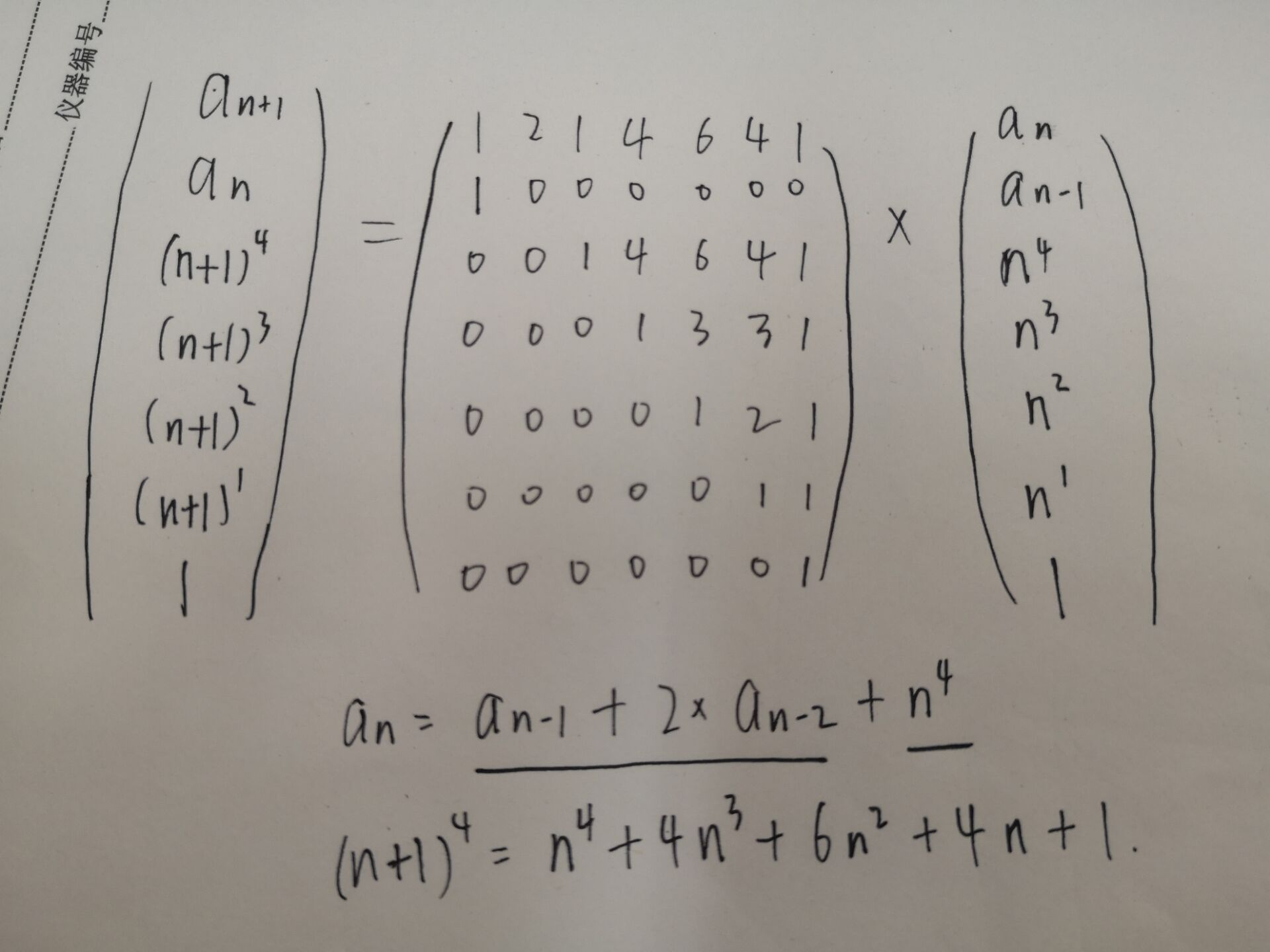HDU - 5950 Recursive sequence(二项式+矩阵合并+矩阵快速幂)
Recursive sequence
InputThe first line of input contains an integer t, the number of test cases. t test cases follow.
Each case contains only one line with three numbers N, a and b where N,a,b < 231231 as described above.
OutputFor each test case, output the number of the N-th cow. This number might be very large, so you need to output it modulo 2147493647.Sample Input
2
3 1 2
4 1 10
Sample Output
85
369
Hint
In the first case, the third number is 85 = 2*1十2十3^4.
In the second case, the third number is 93 = 2*1十1*10十3^4 and the fourth number is 369 = 2 * 10 十 93 十 4^4.
矩阵快速幂。利用了矩阵合并将两个递推关系合并到一个矩阵中。
之前做过了不少含有变量项的题,这道题是底数为变量,指数为常数的一种。
其中变量项的递推利用了二项式定理,系数满足杨辉三角规律。
#include <bits/stdc++.h>
#define MAX 10
#define MOD 2147493647
using namespace std;
typedef long long ll; struct mat{
ll a[MAX][MAX];
}; mat operator *(mat x,mat y)
{
mat ans;
memset(ans.a,,sizeof(ans.a));
for(int i=;i<=;i++){
for(int j=;j<=;j++){
for(int k=;k<=;k++){
ans.a[i][j]+=(x.a[i][k]*y.a[k][j]+MOD)%MOD;
ans.a[i][j]%=MOD;
}
}
}
return ans;
}
mat qMod(mat a,ll n)
{
ll tt[][]={,,,,,,,,
,,,,,,,,
,,,,,,,,
,,,,,,,,
,,,,,,,,
,,,,,,,,
,,,,,,,,
,,,,,,,};
mat t;
for(int i=;i<=;i++){
for(int j=;j<=;j++){
t.a[i][j]=tt[i][j];
}
}
while(n){
if(n&) a=t*a;
n>>=;
t=t*t;
}
return a;
}
int main()
{
int t,i,j;
ll n,a,b;
scanf("%d",&t);
while(t--){
scanf("%I64d%I64d%I64d",&n,&a,&b);
if(n<){
if(n==) printf("%I64d\n",a);
if(n==) printf("%I64d\n",b);
continue;
}
mat x;
memset(x.a,,sizeof(x.a));
x.a[][]=b;
x.a[][]=a;
x.a[][]=***;
x.a[][]=**;
x.a[][]=*;
x.a[][]=;
x.a[][]=;
x=qMod(x,n-);
printf("%I64d\n",x.a[][]);
}
return ;
}
HDU - 5950 Recursive sequence(二项式+矩阵合并+矩阵快速幂)的更多相关文章
- HDU 5950 Recursive sequence 【递推+矩阵快速幂】 (2016ACM/ICPC亚洲区沈阳站)
Recursive sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Other ...
- HDU 5950 Recursive sequence 递推转矩阵
Recursive sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Other ...
- hdu 5950 Recursive sequence 递推式 矩阵快速幂
题目链接 题意 给定\(c_0,c_1,求c_n(c_0,c_1,n\lt 2^{31})\),递推公式为 \[c_i=c_{i-1}+2c_{i-2}+i^4\] 思路 参考 将递推式改写\[\be ...
- HDU 5950 - Recursive sequence - [矩阵快速幂加速递推][2016ACM/ICPC亚洲区沈阳站 Problem C]
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5950 Farmer John likes to play mathematics games with ...
- HDU 5950 Recursive sequence(矩阵快速幂)
题目链接:Recursive sequence 题意:给出前两项和递推式,求第n项的值. 题解:递推式为:$F[i]=F[i-1]+2*f[i-2]+i^4$ 主要问题是$i^4$处理,容易想到用矩阵 ...
- hdu 5950 Recursive sequence 矩阵快速幂
Recursive sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Other ...
- HDU 5950 Recursive sequence(矩阵快速幂)题解
思路:一开始不会n^4的推导,原来是要找n和n-1的关系,这道题的MOD是long long 的,矩阵具体如下所示 最近自己总是很坑啊,代码都瞎吉坝写,一个long long的输入写成%d一直判我TL ...
- hdu 5950 Recursive sequence
题意:告诉你数列的递推公式为f(n+1)=f(n)+2*f(n-1)+(n+1)^4 以及前两项a,b:问第n项为多少,结果对2147493647取模. 题解:有递推公式,马上应该就能想到矩阵快速幂: ...
- Luogu 3390 【模板】矩阵快速幂 (矩阵乘法,快速幂)
Luogu 3390 [模板]矩阵快速幂 (矩阵乘法,快速幂) Description 给定n*n的矩阵A,求A^k Input 第一行,n,k 第2至n+1行,每行n个数,第i+1行第j个数表示矩阵 ...
随机推荐
- PPID=1 runs as a background process, rather than being under the direct control of an interactive user
https://en.wikipedia.org/wiki/Daemon_(computing) [后台进程,非互动] d 结尾 syslogd 系统日志记录 sshd 响应ssh连接请求 In mu ...
- pjax + tp5,实现局部无刷新返回数据
文件1:\application\admin\controller\Setting.php 最后一句代码:要fetch原页面 <?php namespace app\admin\controll ...
- 【题解】[Ghd]
[题解]Ghd 一道概率非酋题? 题目很有意思,要我们选出大于\(\frac{n}{2}\)个数字使得他们的最大公约数最大. 那么我们若随便选择一个数字,他在答案的集合里的概率就大于\(0.5\)了. ...
- 我的Android进阶之旅------>Android通过使用Matrix旋转图片来模拟碟片加载过程
今天实现了一个模拟碟片加载过程的小demo,在此展示一下.由于在公司,不好截取动态图片,因此就在这截取两张静态图片看看效果先. 下面简单的将代码列出来. setp1.准备两张用于旋转的图片,如下:lo ...
- javac 编译源文件出现"java:1: 需要为 class、interface 或 enum"、" [javac] 锘縫"错误
[javac] HelloWorld.java:1: 需要为 class.interface 或 enum [javac] 锘縫ackage com.csdn.demo; [javac] ^ [jav ...
- Flask中的模板语法jinjia2
Flask中默认的模板语言是Jinja2 I. Jinja2模板语言中的 for {% for foo in g %} {% endfor %} II. Jinja2模板语言中的 if {% if g ...
- 3D 图片播放焦点图插件Adaptor
在线演示 本地下载
- Python网络编程--Echo服务
Python网络编程--Echo服务 学习网络编程必须要练习的三个小项目就是Echo服务,Chat服务和Proxy服务.在接下来的几篇文章会详细介绍. 今天就来介绍Echo服务,Echo服务是最基本的 ...
- SQLSERVER2008 R2的端口设置
通过存储过程查看 我们首先打开sqlserver连接sqlserver2008的数据库实例,然后执行如下存储过程: --查询端口号 exec sys.sp_readerrorlog 0, 1, 'li ...
- LightOJ - 1248 Dice (III) —— 期望
题目链接:https://vjudge.net/problem/LightOJ-1248 1248 - Dice (III) PDF (English) Statistics Forum Tim ...