BZOJ 1041 [HAOI2008]圆上的整点：数学【费马平方和定理】

题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=1041

题意：

　　给定n(n <= 2*10^9)，问你在圆x^2 + y^2 = n^2的圆周上，有多少个坐标为整数的点。

题解：

　　科普视频：http://www.bilibili.com/video/av12131743/

　　推导的大致思路：

　　

　　推导：

　　　　一、17 = 4^2 + 1^2

　　　　　　求圆周上有多少个点，就是求有多少个整数对(a,b)满足a^2 + b^2 = R^2。

　　　　二、17 = (4+i)*(4-i)

　　　　　　变形：a^2 + b^2 = (a + b*i) * (a - b*i) = R^2。

　　　　　　其中，a + b*i 与 a - b*i 复共轭。

　　　　　　也就是将R^2分解成(a + b*i) * (a - b*i)。

　　　　　　有一个结论，对于整数a来说：

　　　　　　　　（1）如果a为4n + 1型的素数，则a可以被分解为两个不同的高斯素数。

　　　　　　　　（2）如果a为4n + 3型的素数，则不能被分解。因为它们不仅是普通素数，还是高斯素数。

　　　　　　（即费马平方和定理：只有4n+1型的素数，才能表示成两个数的平方和）

　　　　　　分解方法：

　　　　　　　　（1）首先将R^2分解质因数，R^2 = a1^p1 + a2^p2 +...

　　　　　　　　（2）然后将R^2继续分解成若干高斯素数之积。

　　　　　　　　（3）将这些高斯素数分成两组，如果这两组各自之积复共轭，则为一对合法的(a,b)。

　　　　　　其中，将高斯素数分组时，对于一个素因子ai，有pi+1中分组方法。

　　　　　　特别地，2^k对于最终答案没有影响。

　　　　　　根据乘法原理，在能够分组（分成复共轭数）的前提下，最终的分组方法数 = 4*∏(pi+1)。

　　　　　　（这就是本题的做法。分解质因数，复杂度O(sqrt(N))）

　　　　三、积性函数χ(n)，求π的表达式（这部分跟此题无关）

　　　　　　对于函数χ(n)，定义为：

　　　　　　　　（1）n = 4k + 1时，χ(n) = 1

　　　　　　　　（2）n = 4k + 3时，χ(n) = -1

　　　　　　　　（3）n为偶数时，χ(n) = 0

　　　　　　函数χ(n)对于任意整数满足性质：χ(ab) = χ(a)*χ(b)，所以χ(n)为积性函数。

　　　　　　将圆上点的数量写成如下形式：

　　　　　　

　　　　　　即：N = 4*∏(∑ χ(ki))，ki为R^2的因子。

　　　　　　将上式拆开，每一项χ(n)的n为R的因子：

　　　　　　

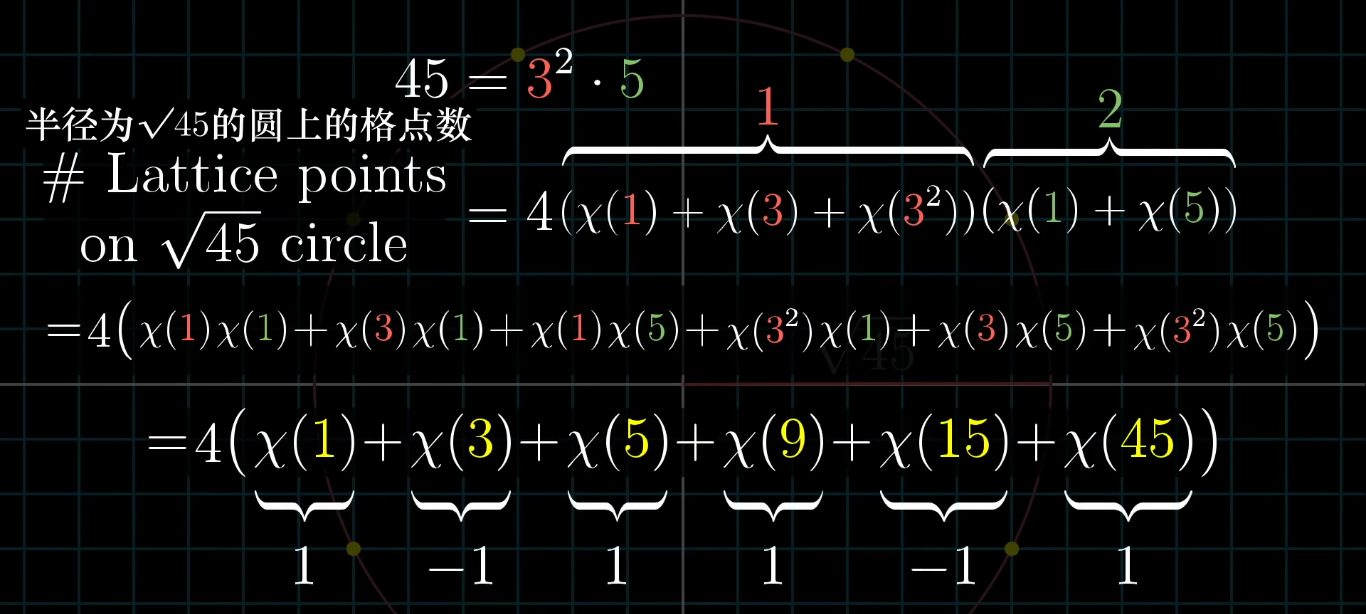
　　　　　　圆内所有点的个数：

　　　　　　

　　　　　　移动之后：

　　　　　　

　　　　　　所以得到了圆内点的个数，也就是圆面积的另一种表达形式。

　　　　　　最终得到了一个π的表达式。

　　　　　　

AC Code:

 #include <iostream>
 #include <stdio.h>
 #include <string.h>

 using namespace std;

 long long n;
 long long ans=;

 int main()
 {
     cin>>n;
     n=n*n;
     long long t=n;
     while(!(t&)) t>>=;
     for(int i=;i*i<=n && t>;i++)
     {
         int p=;
         while(t%i==)
         {
             p++;
             t/=i;
         }
         if(i%==) ans*=(p+);
         else if(i%== && (p&))
         {
             ans=;
             break;
         }
     }
     if(t%==) ans=;
     cout<<ans*<<endl;
 }