算法图解之大O表示法

什么是大O表示法

大O表示法可以告诉我们算法的快慢。

大O比较的是操作数，它指出了算法运行时间的增速。

O(n) 括号里的是操作数。

举例

画一个16个格子的网格，下面分别列举几种不同的画法，并用大O表示法表示

1.  一次画一个格子。O(n)

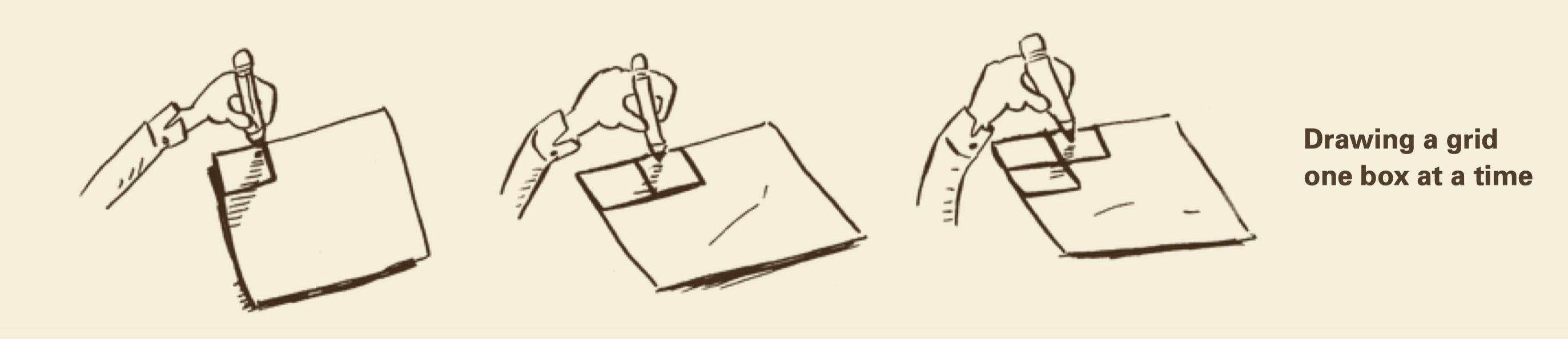
2. 折叠纸张，折叠四次就能出现16个格子。O(log n)

大O表示法所表示的是一个算法在最糟糕情况下的运行时间。

一些常见的大O运行时间

• O(log n)，也叫对数时间，二分查找。

• O(n)，也叫线性时间，简单查找。

• O(n * log n)，快速排序——一种速度较快的排序算法。

• O(n²)，选择排序——一种速度较慢的排序算法。

• O(n!)，旅行商问题的解决方案——一种非常慢的算法。

主要启示

• 算法的速度指的是操作数的增速，而非时间。

• 谈论算法速度说的是随着输入的增加，其运行时间将以什么样的速度增加。

• 用大O表示法表示算法的运行时间。

• 随着元素的增加，快算法比慢算法增加的速度是指数级的。比如，O(log n)和O(n)

旅行商问题

旅行商问题用大O表示法就是O(n!)，没错，就是有这么慢的算法。这个问题是说的一个销售员，要去5个城市，他想规划一下最短距离，然后选出最短的距离。5个城市一共有120种规划方案（5!）。n个城市就有n!种规划方案。旅行商问题在计算机科学领域是无解的。