Codeforces 509E(思维)

                                                                                                                        E. Pretty Song

                                                                                                          time limit per test:1 second

                                                                                                     memory limit per test:256 megabytes

                                                                                                                    input: standard input

                                                                                                                    output:standard output

When Sasha was studying in the seventh grade, he started listening to music a lot. In order to evaluate which songs he likes more, he introduced the notion of the song's
prettiness. The title of the song is a word consisting of uppercase Latin letters. The
prettiness of the song is the
prettiness of its title.

Let's define the simple prettiness of a word as the ratio of the number of vowels in the word to the number of all letters in the word.

Let's define the prettiness of a word as the sum of
simple prettiness of all the substrings of the word.

More formally, let's define the function vowel(c) which is equal to
1, if c is a vowel, and to
0 otherwise. Let s_i be the
i-th character of string
s, and s_i..j be the substring of word
s, staring at the i-th character and ending at the
j-th character (s_isi + 1...
s_j,
i ≤ j).

Then the simple prettiness of
s is defined by the formula:

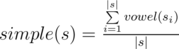
The prettiness of
s equals

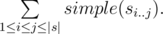
Find the prettiness of the given song title.

We assume that the vowels are I, E, A, O, U, Y.

Input

The input contains a single string s (1 ≤ |s| ≤ 5·10⁵) — the title of the song.

Output

Print the prettiness of the song with the absolute or relative error of at most
10^- 6.

Examples

Input

IEAIAIO

Output

28.0000000

Input

BYOB

Output

5.8333333

Input

YISVOWEL

Output

17.0500000

Note

In the first sample all letters are vowels. The
simple prettiness of each substring is 1. The word of length
7 has 28 substrings. So, the
prettiness of the song equals to
28.

一开始完全没有思路……但是后来想着想着就出来一个O(N)的。要用到预处理。(假设字符串长度为N) 首先把那些元音字母的位置筛出来。

我的代码中的ai表示(1/1+1/N) + (2/2+2/(N-1)) + ... + (i/i+i/(N-i+1)) bi表示1/1+1/2+1/3+...+1/i  (之后我会解释为什么要这样预处理)

每次对于一个元音字母的位置x,无论他在该字符串的前一半还是字符串的后一半，都把他调到前一半的对称位置。(比如说输入的字符串长度为6,我现在要处理的元音字母的位置为5，那么就可以等效成2)，然后利用等效之后的这个x生成一个序列，这个序列是分数，长度为N，其中分母为1,2,3,4,...,N,分子为1,2,3,....,x-1,x,x,x,x-1,...,3,2,1(对就是这样的一个序列现在我们要计算这个序列的和),就利用之前预处理出来的a数组和b数组，在O(1)内就可以实现，然后把每次得到的这个和累加起来，结果就是答案。

#include <bits/stdc++.h>

using namespace std;

#define REP(i,n)                for(int i(0); i <  (n); ++i)
#define rep(i,a,b)              for(int i(a); i <= (b); ++i)
#define dec(i,a,b)              for(int i(a); i >= (b); --i)
#define for_edge(i,x)           for(int i = H[x]; i; i = X[i])

const int N     =    600000      +       10;
const int M     =    10000       +       10;
const int Q     =    1000        +       10;
const int A     =    30          +       1;

char s[N];
int len, cnt;
int c[N];
double a[N], b[N];
int l, r;
double ans;
int x;

int main(){

	scanf("%s", s + 1);
	len = strlen(s + 1); cnt = 0;

	l = 0; r = len + 1;
	a[0] = b[0] = 0;
	rep(i, 1, len) b[i] = b[i - 1] + (double)1 / (double)i;

	if (len & 1){
		rep(i, 1, len >> 1){
			++l, --r;
			a[i] = a[i - 1] + i / (double)l + i / (double)r;
		}
		a[len / 2 + 1] = a[len / 2] + (++l) / (len / 2 + 1);
	}
	else{
		rep(i, 1, len >> 1){
			++l, --r;
			a[i] = a[i - 1] + i / (double)l + i / (double)r;
		}
	}

	rep(i, 1, len){
		if (s[i] == 'A' || s[i] == 'E' || s[i] == 'I' || s[i] == 'O' || s[i] == 'U' || s[i] == 'Y'){
			c[++cnt] = i;
		}
	}

	ans = 0;
	rep(i, 1, cnt){
		x = c[i];
		if (x > len / 2) x = len - x + 1;
		if (x <= len / 2) ans += a[x] + (b[len - x] - b[x]) * x;
		else ans += a[x];
	}

	printf("%.7f\n", ans);

	return 0;

}