Codeforces Round #266 (Div. 2) C. Number of Ways

You've got array a[1], a[2], ..., a[n], consisting of
n integers. Count the number of ways to split all the elements of the array into three contiguous parts so that the sum of elements in each part is the same.

More formally, you need to find the number of such pairs of indices
i, j (2 ≤ i ≤ j ≤ n - 1), that
.

Input

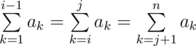The first line contains integer n
(1 ≤ n ≤ 5·10⁵), showing how many numbers are in the array. The second line contains
n integers a[1],
a[2], ..., a[n]
(|a[i]| ≤  10⁹) — the elements of array
a.

Output

Print a single integer — the number of ways to split the array into three parts with the same sum.

Sample test(s)

Input

5
1 2 3 0 3

Output

2

Input

4
0 1 -1 0

Output

1

Input

2
4 1

Output

0

思路：若平分分成若干种情况。应当总体（SUM）考虑，对SUM/3进行分析。它是区分3段的标准。

所以当部分和tmp==SUM/3,部分统计加一。

当tmp==sUM*2/3。则所有统计ans+=部分统计（s）;

#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<cmath>
#include<algorithm>
#define LL  __int64
#define inf 0x3f3f3f3f
using namespace std;
LL a[1000000];
int main()
{
    LL n,m,i,j,k;
    LL b,t;
    while(~scanf("%I64d",&n))
    {
        LL z=0;
        for(i=0;i<n;i++)
        {
            scanf("%I64d",&a[i]);
            z+=a[i];
        }
        if(z%3)
        {
            printf("0\n");
            continue;
        }
        z/=3;
        LL ans=0;LL s=0;LL tmp=0;
        for(i=0;i<n-1;i++)//注意舍去最后以为数<span id="transmark"></span>
        {
            tmp+=a[i];
            if(z*2==tmp)
            {
                ans+=s;
            }
            if(z==tmp)
            {
                s++;
            }
        }
        printf("%I64d\n",ans);
    }
    return 0;
}