UVA 221 城市化地图（离散化思想）

题意：

给出若干个栋楼俯视图的坐标和面积，求从俯视图的南面（可以视为正视图）看过去到底能看到多少栋楼。

输入第一个n说明有n栋楼，然后输入5个实数（注意是实数），分别是楼的左下角坐标（x，y）， 然后楼的x方向的宽度，y方向的深度，还有楼的高度。

按横坐标，横坐标同样按纵坐标排序输出所有能看到的楼。

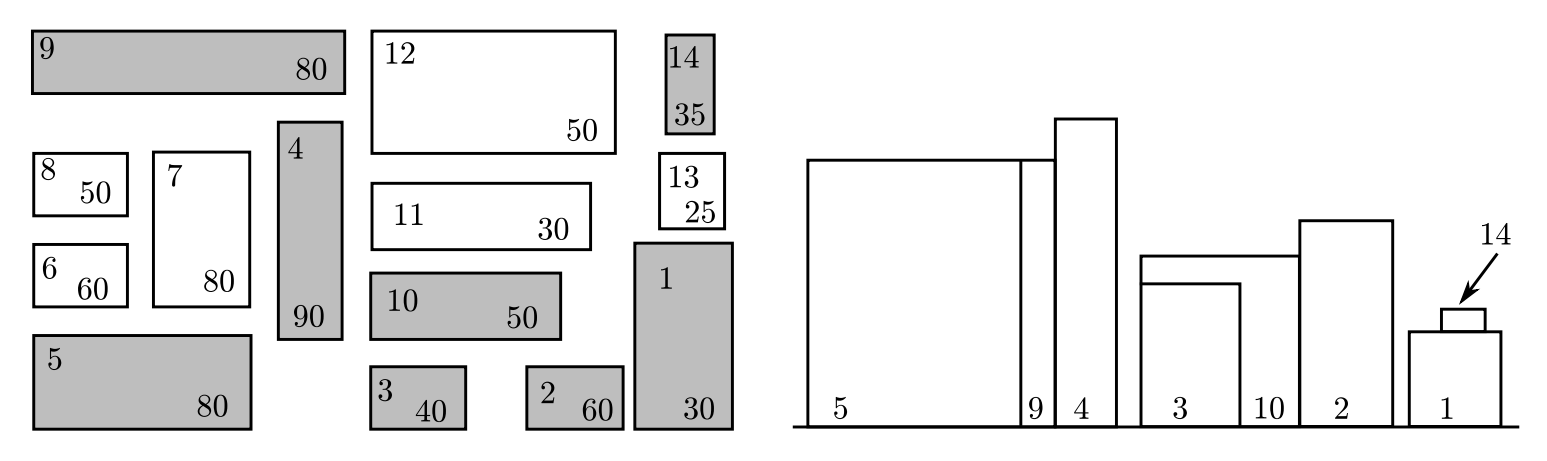
分析：

先记录一个一开始就想错的做法：

以为只要把x 和 width放大到到足够大（例如10000倍，倍数越高精度越高），然后排序填充一下数轴就可以，就可以解决x坐标是小数的问题。但这样打了一下，发现第一计算速度很慢(放大后n倍计算量也同时放大n^2倍）， 第二是无法处理覆盖与重叠的部分， 只会保留数轴中最大的部分， 无法保留在高楼南边的矮楼，第三这种做法也是错误的，只要他是连续的，就算放大也不能完全保证算法正确性。

正确的做法应该是将正视图x轴离散化：

首先这题楼的可见性可以简化成建筑物南面的墙的可见性（可在上图感受一下），所以输入的深度这个属性是没有用的，可以用%*lf（在键盘上读取但不保存）在输入时忽略掉。

接下来就是离散化的核心，提取正视图x轴有用的点，先无限个x的取值化为有限的关键点。

——按每栋楼的x的最左边和最右边看成区间的两个端点， 然后将整张图分为多个区间， 然后可以保证每个区间整片区间一定包含其中一栋楼， 只要判断这个区间包含的楼是否可见即可。

分割如下：

可以观察， 每个区间的任何一个点都拥有同样的性质，即无论从区间的哪一个点观察，都可得到同样的结果。

不妨取每个区间的中点作为关键点

可以先按输出要求遍历所有的楼，每栋楼再遍历所有的区间，然后再判断能否被看见。

如何判断是否能看见？

看见只要满足两个条件：

设这栋楼为A。

①A在其中一个区间内（或者说忽略高度条件，在这个区间的中点能看见A）， 即 楼的最左端 <=该区间中点 && 楼的最右端>=该区间中点 

②该区间内比A的y坐标小的楼都比A矮。（如果在A的南面有比他高的，那么自然看不见A）

　　这个点又可以判断为两个条件

　　1.是否有楼在这个区间内（判断方法同①，所以这种需要重复判断的条件最好写成一个函数）

　　2.该楼是否比A矮（判断一下高度即可）

此外这题还涉及一个STL函数，unique，它通常使用在sort后的数组， 将不同的元素保留在数组前面， 然后那些重复元素移到后面。原型可以为unique(v.begin(),v.end()); 

如果想更深入了解离散化思想可以看看matrix67的博客——http://www.matrix67.com/blog/archives/108

 #include<bits/stdc++.h>
 using namespace std;
 struct Bd
 {
     double x,y, width, high;
     int num;
     bool operator < (const Bd& rhs)const{
         return x<rhs.x ||(x==rhs.x && y < rhs.y);
     }
 }b[];
 int n;
 bool can_see(int i, int mx)//判断第i栋楼在不在中点上
 {
     return b[i].x <= mx && (b[i].x + b[i].width >= mx);
 }
 bool visible(int i, int mx)//包含高度条件，在中点能不能看到第i栋楼
 {
     if(!can_see(i, mx)) return false;
     for(int k = ; k < n;k++)
     {
         if(b[k].y < b[i].y && b[k].high >= b[i].high && can_see(k,mx)) return false;
     }
     return true;
 }
 int main()
 {
     #if LOCAL
     freopen("1.txt","r",stdin);
     #endif // LOCAL
     int kase = ;
     while(scanf("%d", &n) && n)
     {
         double w[];
         for(int i = ; i < n ; i++)
         {
             double tx, ty, tw, th;
             scanf("%lf %lf %lf %*lf %lf", &tx, &ty, &tw, &th);
             b[i].x = tx;
             b[i].y = ty;
             b[i].width = tw;
             b[i].high = th;
             b[i].num = i+;
             w[i*] = tx;
             w[i*+] = tx + tw;
         }
         sort(b,b+n);
         sort(w,w+*n);
         int m = unique(w,w+*n) - w;
         if(kase != ) printf("\n");
         printf("For map #%d, the visible buildings are numbered as follows:\n%d",kase++, b[].num);//第一栋楼在左下角，肯定能看到
         for(int i = ; i < n; i++)
         {
             int is = ;
             for(int j = ; j < m - ; j++)
             {
                 if(visible(i,(w[j]+w[j+])/))
                 {
                     is = ;
                     break;
                 }
             }
             if(is) printf(" %d", b[i].num);
         }
         printf("\n");
     }
 }