java数据结构和算法04（链表）

　　前面我们看了数组，栈和队列，大概就会这些数据结构有了一些基本的认识，首先回顾一下之前的东西；

　　在数组中，其实是分为有序数组和无序数组，我简单实现了无序数组，为什么呢？因为有序数组的实现就是将无序数组进行排序就可以了！后面我想把所有排序给弄在一起说说，而且有序数组这里的序我认为是排序的序，而不是顺序的序，在有序数组中，对插入的数据会进行一种排序，让数组中的元素以一种我们规定的顺序排列，所以插入数据一般效率比较差，然后查找的话就用二分查找等算法，速度很快；

　　在栈和队列中，我们都是用数组来实现的，无非就是怎么实现插入数据和删除数据的一些算法，很容易；

　　我们仔细想想，只要是基于数组实现的数据结构只要是删除和查找效率都很慢，为什么呢？因为删除了数组中的一个元素，就要把这个元素后面的所有数据都向前移动一个位置，当这个数组很大的时候，移动数据这个动作就极大的浪费时间，而查找数据的话速度很快，因为可以直接由下标取数据；假如还要实现各种有序数组，优先级队列，那么增加数据的算法又是一个比较大的问题，效率感人，但是查找的话效率会很快；

　　显而易见，数组只能突出一方面的性能而放弃另外一个点的性能，我们这篇说的链表也是差不多这样的一个东西，链表相对于数组来说，增加和删除数据很容易，但是查询数据就很慢；

　　这里我们只说单链表，有序链表，双向链表这三种简单的链表

1.链表的原理

　　我们对集合和链表应该有一定的了解，集合的本质就是基于数组实现的，我们在ArrayList这个类中就是对一个Object[]这样的一个数组进行操作；而链表LinkedList的本质就是类的组合，在LinkedList这个类中有一个属性是Node，这个节点类（Node）的话有两个指针分别指向前一个节点和后一个节点（当然这是对于双向链表来说的），这样的话我们就可以通过第一个节点的指针找到下一个节点，一直找到最后一个节点；

　　随意画一个图（基于双向链表）：

　　上图有是三个节点，但是节点用代码表示是什么呢？我们就随便看看JDK中LinkedList中的Node类：

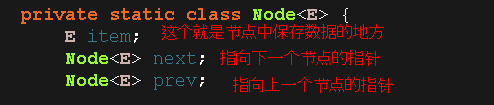
　　而在LinkedList这个了类有两个指针分别指向第一个节点和最后一个节点，功能的话其实就是为了将这一个一个零散的节点建立联系，具体的怎么建立联系呢？我们就慢慢往后看！

2.单链表

　　单链表可以说是结构最简单的链表了，我们先看看结构图，和双向链表不同，只能由一个节点指向下一个节点，是单向的，不能指向上一个节点

　　假如要删除某个节点如下图所示，而增加节点就是删除节点的逆过程；

　　

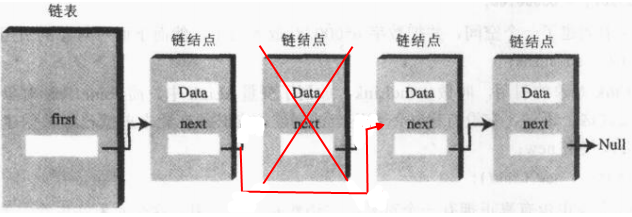
　　我们可以看看LinkedList的源码，可以看到Node类被定义为了一个静态内部类，我们这里也用静态内部类来试试；

　　我们自己的单链表MyLinkedList中简单实现增删改查功能；

package com.wyq.test;

public class MyLinkedList {
    //链表的大小
    private int size;
    //指向链表头节点的指针
    private Node head;

    //初始化的时候啥都没有
    public MyLinkedList(){
        head=null;
        size=0;
    }
    //一个节点的静态内部类，两个属性，一个存数据，一个指向下一个节点的指针
    private static class Node{
        Object obj;
        Node next;

        public Node(Object obj){
            this.obj = obj;
        }
        //展示节点数据
        public void displayNode(){
            System.out.println("{"+obj.toString()+"}");
        }

    }
    //在链表头添加节点
    public int addHead(Object obj){
        Node addNode = new Node(obj);
        if (size==0) {
            head = addNode;
        }else{
            addNode.next=head;
            head=addNode;
        }
        size++;
        return 1;
    }
    //删除链表头的节点
    public int deleteHead(){
        if (size>0) {
            head = head.next;
            return 1;
        }
        return 0;
    }
    //根据一个数据找到链表中存放该数据的节点
    public Node find(Object obj){
        Node cur = head;
        while(size>0){
            if (obj.equals(cur.obj)) {
                return cur;
            }else{
                cur = cur.next;
            }
        }
        return null;
    }
    //找到对应的节点并删除
    public int deleteNode(Object obj){
        Node before = null;
        Node current = head;
        //如果链表为空，返回0
        if (size==0) {
            return 0;
        }
        //如果当前节点的数据不是我们要找的，那就循环，使得指向当前节点的指针后移
        while(!current.obj.equals(obj)){
            if (current.next==null) {
                return 0;
            }else{
                before = current;
                current = current.next;
            }
        }
        //如果链表中只有一个节点，那就删除第一个节点，也就是将头指针指向null
        //如果有多个节点，首先前面while循环就已经找到该目的节点了，我们将该节点剔除，也就是将前一个节点和后一个节点连起来就ok了
        if (size==1) {
            head = head.next;
            size=0;
            return 1;
        }else{
            before.next = current.next;
            size--;
            return 1;
        }
    }
    //链表的大小
    public int size(){
        return size;
    }
    //循环展示链表中每一个节点中的数据
    public void display(){

        Node cur = head;
        while(cur!=null){
            cur.displayNode();
            cur = cur.next;
        }
    }
    public static void main(String[] args) {
        MyLinkedList linkedList = new MyLinkedList();
        linkedList.addHead("hello world");
        linkedList.addHead(123);
        linkedList.addHead('a');
        linkedList.addHead(false);

        linkedList.deleteNode(123);
        linkedList.display();
        System.out.println(linkedList.size());
    }
}

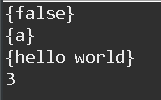
3. 有序链表

　　讨论至今，还没有要求链表中要实现有序，只是再某些特殊情况需要保持有序，个人认为有序链表了解即可，一般情况下把一个链表弄成有序的性价比不高；

　　前面我们实现的链表是无序链表，因为链表中的数据没有什么顺序；

　　有序链表的话，就要在我们向链表中添加数据的时候，会从第一个节点开始，比较每一个节点中的数据，并确定应该添加的数据存放的位置，我们只需要对上面的那个例子做一点小小的改造即可，就选取其中的增加和删除方法进行改造；

　　顺便一提，由于有序链表在添加数据的时候要一个一个的比较，所以相对于无序链表，添加数据略慢一点；

package com.wyq.test;

public class OrderLinkedList {
    //链表的大小
    private int size;
    //指向链表头节点的指针
    private Node head;

    //初始化的时候啥都没有
    public OrderLinkedList(){
        head=null;
        size=0;
    }
    //一个节点的静态内部类，两个属性，一个存数据，一个指向下一个节点的指针
    private static class Node{
        int value;
        Node next;

        public Node(int value){
            this.value = value;
        }
        //展示节点数据
        public void displayNode(){
            System.out.println("{"+value+"}");
        }

    }
    //让链表中的元素从小到大排列
    //这个方法是最关键的方法，向有序链表中添加数据怎么样能使得有序呢？我们可以简单看看这个方法，这里最重要的就是两个指针before和current，最初由于一个节点都
    //没有，所以before指向null，而current指向头节点head，head其实为null
    //在我们添加第一个节点的时候，会进入for语句中，其实就是用head保存新节点的引用；此时before=null,current=addNode
    //我们添加第二个节点，这里有两种可能；（1）第一种是比第一个节点数据小，这种不会走while循环，走if语句，这种方案就是相当于表头添加节点
    //（2）第二个节点数据比第一个大，那就首先进入while循环，循环一次后before=head，current=null跳出循环，然后走else语句，
    //最后就是将第二个节点连接在第一个节点的后面，后面添加第三、第四等等节点就按照这个套路。。。
    public int add(int val){
        Node addNode = new Node(val);
        Node before = null;
        Node current = head;
        while(current!=null && val>current.value){
            before = current;
            current = current.next;
        }
        if (before == null) {
            head = addNode;
            head.next = current;
            size++;
            return 1;
        }else{
            before.next = addNode;
            addNode.next = current;
            size++;
            return 1;
        } 

    }
    //删除链表头的节点
    public int deleteHead(){
        if (size==0) {
            return 0;
        }
        head = head.next;
        size--;
        return 1;
    }
    //链表的大小
    public int size(){
        return size;
    }
    //循环展示链表中每一个节点中的数据
    public void display(){

        Node cur = head;
        while(cur!=null){
            cur.displayNode();
            cur = cur.next;
        }
    }
    public static void main(String[] args) {
        OrderLinkedList order = new OrderLinkedList();
        order.add(3);
        order.add(100);
        order.add(1);
        order.add(50);
        order.add(20);

        order.deleteHead();

        order.display();
        System.out.println(order.size());

    }
}

　　

4.双向链表

　　双向链表又是什么呢？我们前面介绍的单链表和有序链表有没有发现只能从前往后一个一个的遍历，但是不能从后往前遍历，双向链表就是正向和逆向两个方向都可以遍历！我们很熟悉的链表LinkedList就是一个双向链表，有兴趣的可以去看看源码；

　　随便借一张图看看原理，可以看到每一个节点都有两个指针，这样的话明显原理就稍微复杂一点，而且相对于单链表，插入和删除数据效率略微降低，因为要修改双倍的指针引用

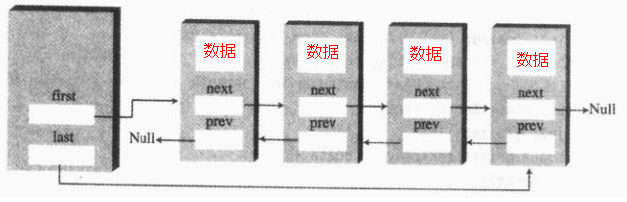
　　在表头添加新的节点原理如下：

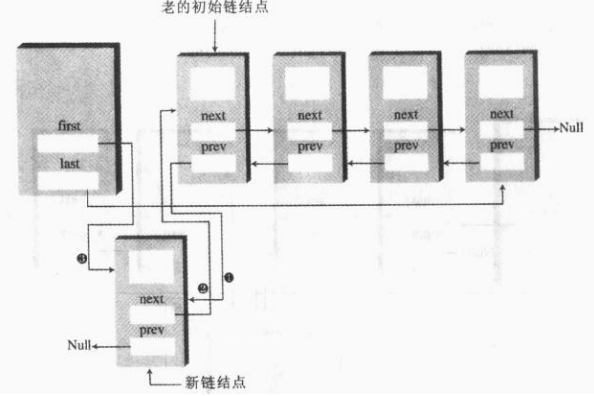
　　其实知道了在表头添加节点之后，在中间指定的位置添加节点也是差不多的，只是将新节点的prev属性指向前一个节点，前一个节点的next指向新节点，所以就不多说了；

　　什么都是虚的，还是用代码来简单实现一下这其中的原理：

package com.wyq.test;

public class MyLinkedList {
    //链表的大小
    private int size=0;
    //指向链表头节点的指针
    private Node first;
    //指向链表尾节点的指针
    private Node last;

    //初始化的时候啥都没有,两个指针都为空
    public MyLinkedList(){
        first=null;
        last=null;
    }
    //一个节点的静态内部类，三个属性，一个存数据，两个指针
    private static class Node{
        Object obj;
        Node pre;
        Node next;

        public Node(Object obj){
            this.obj = obj;
        }
        //展示节点数据
        public void diaplayNode(){
            System.out.println("{"+obj.toString()+"}");
        }
    }

    //在表头增加节点
    public void addHead(Object obj){
        Node newNode = new Node(obj);
        //假如链表中没有节点，那就将这个newNode当作第一个ie节点，同时也是最后一个节点
        if (size==0) {
            first = newNode;
            last = newNode;
            size++;
        }else{
        //如果链表中已经有了很多的节点，我们先把newNode和first节点相互关联起来，再把first指针指向newNode，此时newNode就是表头
            first.pre = newNode;
            newNode.next = first;
            first = newNode;
            size++;
        }
    }
    //删除表头节点，可以返回被删除的节点
    public Node deleteHead(){
        Node temp = first;
        //如果链表中有多个节点，就把first指针往后移动一个节点，此时的first指向的节点的前面赋值为null
        if (size>0) {
            first = first.next;
            first.pre = null;
            size--;
        }
        return temp;
    }

    //在表尾增加节点
    public void addLast(Object obj){
        Node newNode = new Node(obj);
        //如果链表中没有节点，此时的newNode节点是头节点也是尾节点
        if (size==0) {
            first = newNode;
            last = newNode;
            size++;
        }else{
            //链表中有多个节点，那么就把newNode节点于最后的节点last相互关联，移动last指针指向newNode即可
            newNode.pre = last;
            last.next = newNode;
            last = newNode;
            size++;
        }
    }
    //删除尾节点，并返回被删除的节点
    public Node deleteLast(){
        Node temp = last;
        //如果链表中有很多节点，那么先得到倒数第二个节点，根据倒数第二个节点对最后的那个节点赋值为null
        if (size>0) {
            last = last.pre;
            last.next = null;
            size--;
        }
        return temp;
    }

    //显示节点个数
    public int size(){
        return size;
    }
    //展示双向链表中的所有数据
    public void display(){
        if (size>0) {
            //通过一个无限循环来打印每一个节点中的信息
            Node temp = first;
            while(temp!=null){
                temp.diaplayNode();
                temp = temp.next;
            }

        }else{
            System.out.println("[]");
        }
    }

    public static void main(String[] args) {
        MyLinkedList myLinkedList = new MyLinkedList();
        myLinkedList.addHead("hello world");
        myLinkedList.addHead("你好");
        myLinkedList.addHead(1234);
        myLinkedList.addHead(false);
        myLinkedList.addHead("链表的开始");

        myLinkedList.addLast("链表的最后");
        myLinkedList.display();
        System.out.println(myLinkedList.size());

        System.out.println("-----------------------------------------");

        myLinkedList.deleteHead();
        myLinkedList.deleteLast();
        myLinkedList.display();

        System.out.println(myLinkedList.size());
    }

}

 5.总结

　　对于链表的实现有点难度，其实就是那些指针的指向，在增加、删除节点的时候指针的变化很无奈，只能慢慢理解，最重要的是最后的那个双向链表，这个也是我们用的最多的！还有链表和数组的区别要理解，个人感觉最大的区别就是删除和查询这两个操作。

　　对于数组：删除某一个数据，其他的数据都要往前移动一个位置以填补删除的空缺，效率比较慢；但是查询的话速度很快，直接通过下标就可以很快的查到；

　　对于单链表：删除某一个节点数据很快，只需要改变上下节点的引用，但是要根据某一个数据查询该节点的位置，就需要从第一个节点慢慢的next，知道找到目标节点；

　　对于有序链表：就是在单链表的基础上，使得链表中的数据以一定的顺序排列，这种链表插入数据的时候要一个一个的和每一个节点的数据比较，直到找到适当的位置，所以插入数据的效率比较慢；

　　对于双向链表：这种链表差不多可以说是在单链表的基础上又增加了一些特性，就是可以从一个节点访问上一个节点。