《深入浅出深度学习：原理剖析与python实践》第八章前馈神经网络（笔记）

8.1 生物神经元（BN）结构

1、人脑中有100亿-1000亿个神经元，每个神经元大约会和其他1万个神经元相连

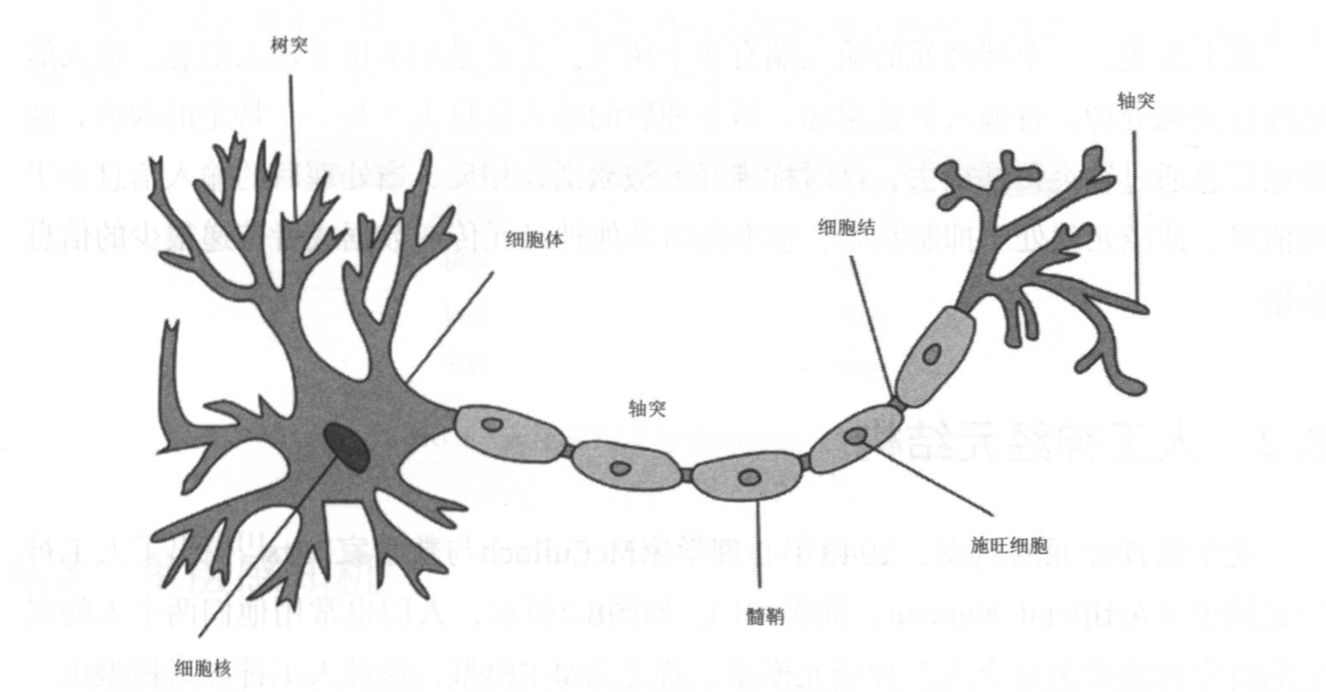
2、细胞体：神经元的主体，细胞体=细胞核+细胞质+细胞膜，存在膜电位

3、树突：从细胞体向外延伸出许多突起的神经纤维。输入端

4、轴突：细胞体伸出的最长的一条突起，也叫神经纤维。长而细。末端细分支为神经末梢。输出端

5、突触：一个神经元轴突的神经末梢和另一个神经元的细胞体或树突进行通信连接。

6、神经传导流程：多个树突接受输入信息，输入信息累加大于某一个特定阈值，信息通过轴突传播出去，神经元被激活。否则，若输入信息小于阈值，神经元处于抑制状态。

8.2 人工神经元模型（AN/M-P模型）

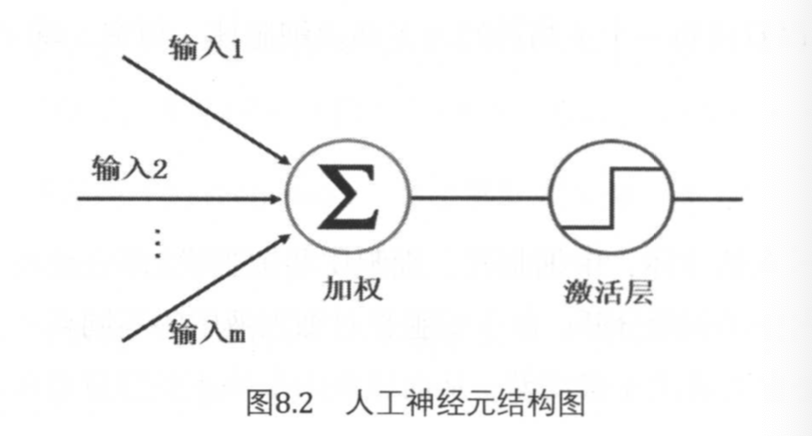
1、AN处理数据流程

　　预激活阶段：接受来自其他m个神经元传递过来的输入信号，这些输入信号通过与相应权重进行加权求和传递给下一阶段

　　h = b + ( _i∑w_i × x_i )  i=1...m　　

　　第二阶段：将预激活的加权结果传递给激活函数，经过激活函数处理，预激活的数据被压缩到一个范围区间内，数值的大小决定神经元处于活跃状态还是抑制状态，输出结果传递给下一层的神经元

　　a = ƒ ( h )

生物神经元	人工神经元
细胞核	神经元
树突	输入
轴突	输出
突触	权重

8.3 单层感知机

1、单层感知机是1957年由计算机科学家Rosenblatt提出的神经网络模型，由输入层和输出层构成

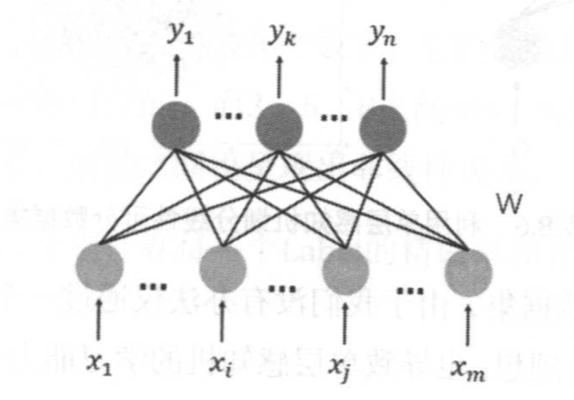
2、Perceptron由m个输入神经元和n个输出神经元构成，是一个全连接的二分图结构。

　　（1）单层感知机在输入层接收数据，把输入数据与相应权重参数累加

　　　　　　h_k = b_k + ( _i∑w_ik × x_i ) k = 1...n.  i = 1...m

　　（2）将累加结果输入到激活函数中，单层感知机的输出层可以采用Logistic/softmax函数作为最后的结果输出

　　　　　　y_k = softmax(h_k)  k = 1...n

3、感知机的工作原理：本质是在高维空间中，构造出合理的边界超平面（b + ∑w_ix_i），把不同类别的数据集分离。对于线性可分或近似线性可分的数据集有很好的效果。对于线性不可分数据集，效果不理想。

8.4 多层感知机

1、理论依据：1991年Kurt Hornik提出的全局逼近定理----对于含有一个隐藏层的前馈神经网络，如果隐藏层可以由任意多的神经元构成，那么神经网络能够逼近实数范围内的任意连续函数。

简而言之，对于分类问题，隐藏层的作用就是把线性不可分的数据，通过线性变换（预激活阶段）和非线性的激活（激活阶段）的操作，使得数据在输出层变成线性可分

2、神经网络中包含的隐藏层越深，隐藏层包含的神经元越多，它能提取的特征就越丰富，就具备更强大的学习能力，但是实际上，随着网络逐渐加深，神经网络的性能在达到一个极值后（一般两到三层），就停止提升。

8.5 激活函数

1、激活态：处在活跃状态的神经元

2、抑制态：处在非活跃状态的神经元

3、隐藏层神经元中引入了激活函数使MLP模型能力提升。如果多层神经网络只添加隐藏层，而没有添加激活函数，或者激活函数是线性函数，那么MLP等价于单层感知机。

4、激活函数在神经网络中的作用

（1）非线性的激活函数使得模型能够处理更加复杂的非线性数据集问题，提高了模型的学习能力

（2）通过激活函数的处理，神经元被划分为激活态和抑制态，因此，在训练的过程中，能够把重点的神经元置为激活态，把相对无关的神经元置为抑制态，自动特征提取。

5、激活函数性质：非线性、可微性、单调性

6、常用激活函数

（1）阶跃函数：不连续、不光滑、不可导

（2）sigmoid函数和tanh函数：有缺陷

（3）近似生物神经元的激活函数：例ReLU和softplus