HDU_1227_Fast Food_动态规划

链接：http://acm.hdu.edu.cn/showproblem.php?pid=1227

Fast Food

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2695    Accepted Submission(s): 1142

Problem Description

The fastfood chain McBurger owns several restaurants along a highway. Recently, they have decided to build several depots along the highway, each one located at a restaurant and supplying several of the restaurants with the needed ingredients. Naturally, these depots should be placed so that the average distance between a restaurant and its assigned depot is minimized. You are to write a program that computes the optimal positions and assignments of the depots.

To make this more precise, the management of McBurger has issued the following specification: You will be given the positions of n restaurants along the highway as n integers d1 < d2 < ... < dn (these are the distances measured from the company's headquarter, which happens to be at the same highway). Furthermore, a number k (k <= n) will be given, the number of depots to be built.

The k depots will be built at the locations of k different restaurants. Each restaurant will be assigned to the closest depot, from which it will then receive its supplies. To minimize shipping costs, the total distance sum, defined as

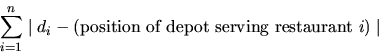
must be as small as possible.

Write a program that computes the positions of the k depots, such that the total distance sum is minimized.

 

Input

The input file contains several descriptions of fastfood chains. Each description starts with a line containing the two integers n and k. n and k will satisfy 1 <= n <= 200, 1 <= k <= 30, k <= n. Following this will n lines containing one integer each, giving the positions di of the restaurants, ordered increasingly.

The input file will end with a case starting with n = k = 0. This case should not be processed.

 

Output

For each chain, first output the number of the chain. Then output a line containing the total distance sum.

Output a blank line after each test case.

 

Sample Input

6 3
5
6
12
19
20
27
0 0

 

Sample Output

Chain 1
Total distance sum = 8

 

一来没思路，看了题解，目前动态规划的题几乎都看了题解才有思路。。。。。。

思路：[i,j]之间加一个仓库，为了使要增加的路程最短，只能加在第(int)(i+j)/2个餐厅。

case[i][j]为在[i,j]之间加一个仓库所要增加的路程。

dp[i][j]表示在前j个餐厅之中加i个仓库所要走的路程。

状态转移方程：dp[i][j]=min(dp[i][j],dp[i-1][m]+case[m+1][j]);  （i-1<=m<=j-1）

 

#include<iostream>
#include<cstdio>
#include<stdlib.h>
#include<cstring>
using namespace std;
#define LL long long

int dis[];
int dist[][];
int dp[][];

int main()
{
    int n,k,cases=;
    while(scanf("%d%d",&n,&k)!=EOF&&n&&k)
    {
        memset(dist,,sizeof(dist));

        for(int i=; i<=k; i++)
            for(int j=; j<=n; j++)
                dp[i][j]=;
                //cout<<dp[0][0];
        dp[][]=;
        dp[][]=;
        for(int i=; i<=n; i++)
            scanf("%d",&dis[i]);
        for(int i=; i<=n-; i++)
            for(int j=i; j<=n; j++)
            {
                int mid=(i+j)/;
                for(int k=i; k<=j; k++)
                    dist[i][j]+=abs(dis[mid]-dis[k]);
            }
        for(int i=;i<=n;i++)
            dp[][i]=dist[][i];
        for(int j=; j<=n; j++)
            for(int i=; i<=j,i<=k; i++)
                for(int m=i-; m<=j-; m++)
                    dp[i][j]=min(dp[i][j],dp[i-][m]+dist[m+][j]);

        printf("Chain %d\n",cases++);
        printf("Total distance sum = %d\n\n",dp[k][n]);
    }
    return ;
}