CMU Database Systems - Two-phase Locking

首先锁是用来做互斥的，解决并发执行时的数据不一致问题

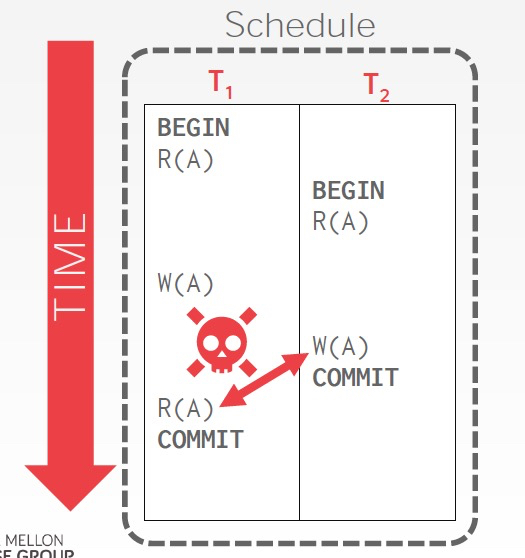
如图会导致，不可重复读

如果这里用lock就可以解决，数据库里面有个LockManager来作为master，负责锁的记录和授权

数据库里面的基本的锁类型，

其实就是读锁，写锁

但是如果光是有读写锁，只能解决当个操作互斥和正确，无法解决transaction的正确

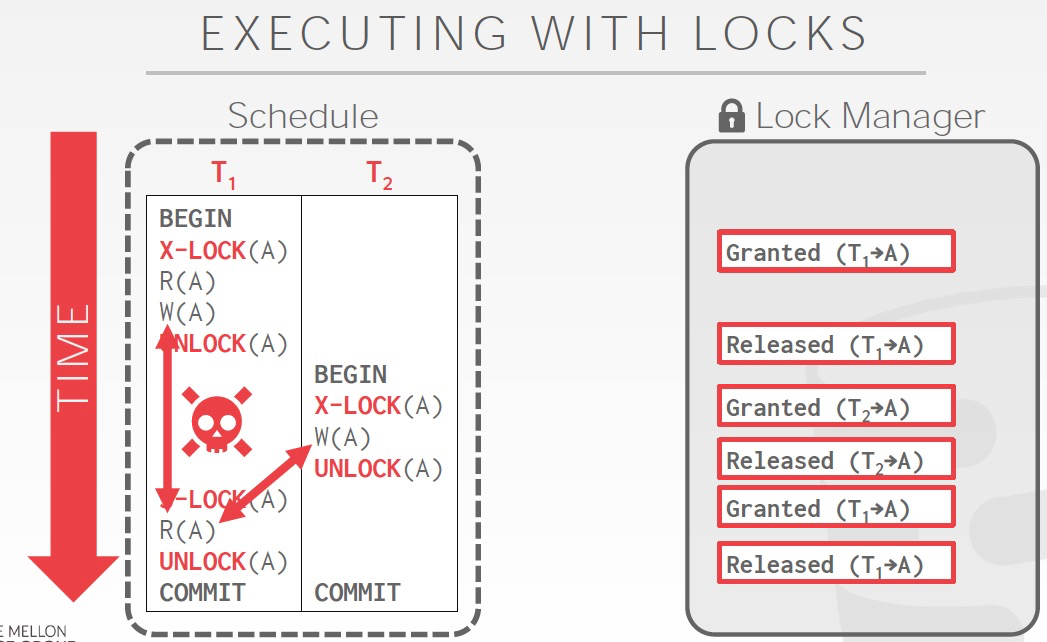
所以我们需要一个事务级别的锁，就是2PL，两阶段提交

最核心的想法，在growing阶段需要拿到所有需要的锁，否则就会block；shrinking阶段，不能去增加锁，只能释放锁

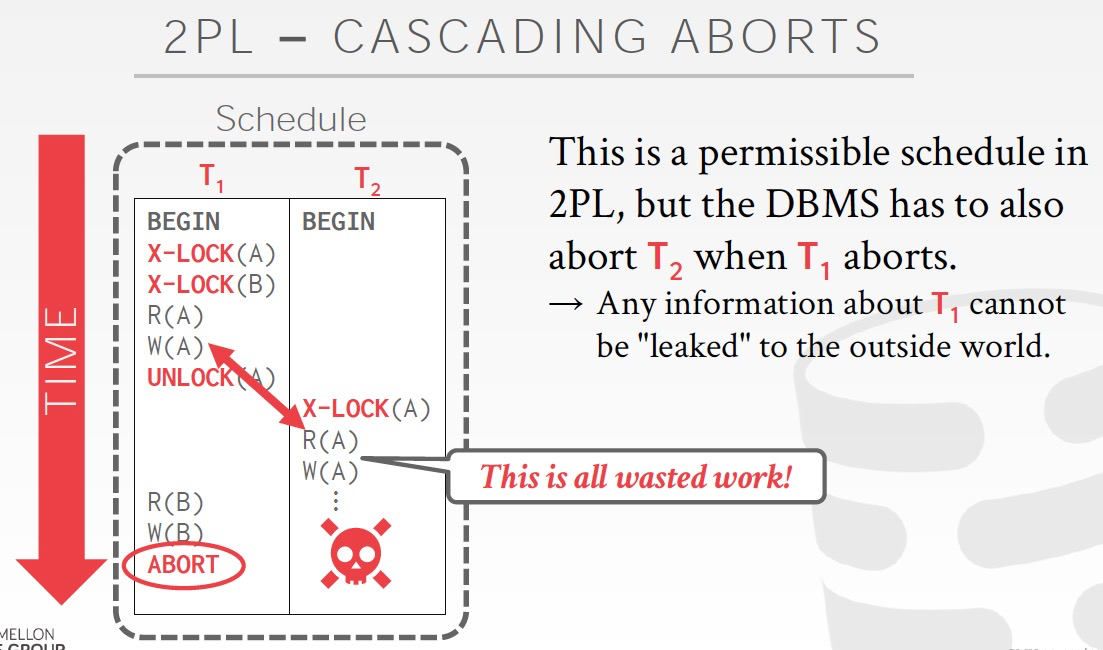
2PL在shrinking阶段是可以逐个去释放锁的，这样会有cascding aborts问题

因为你释放部分锁的时候，其他的事务就会看到你的改动，但最终你abort，那么所有相关的事务由于脏读也必须要abort

2PL有如下的问题，

首先，2PL是充分不必要条件，不满足2PL并不一定会导致调度问题，所以2PL限制了并发

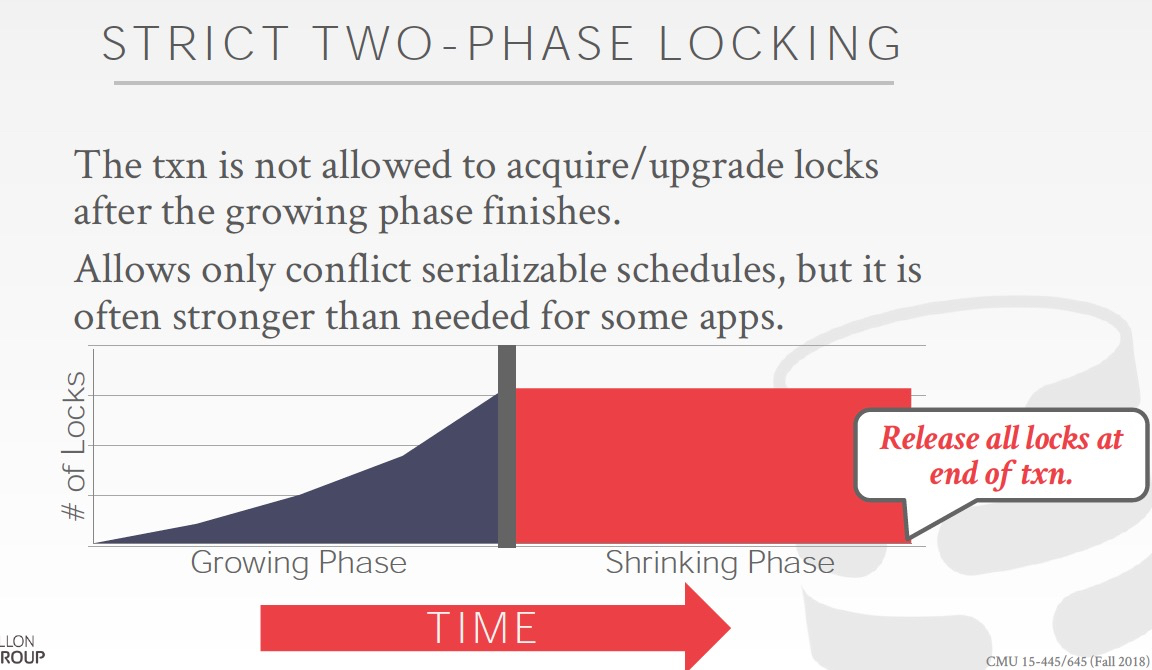
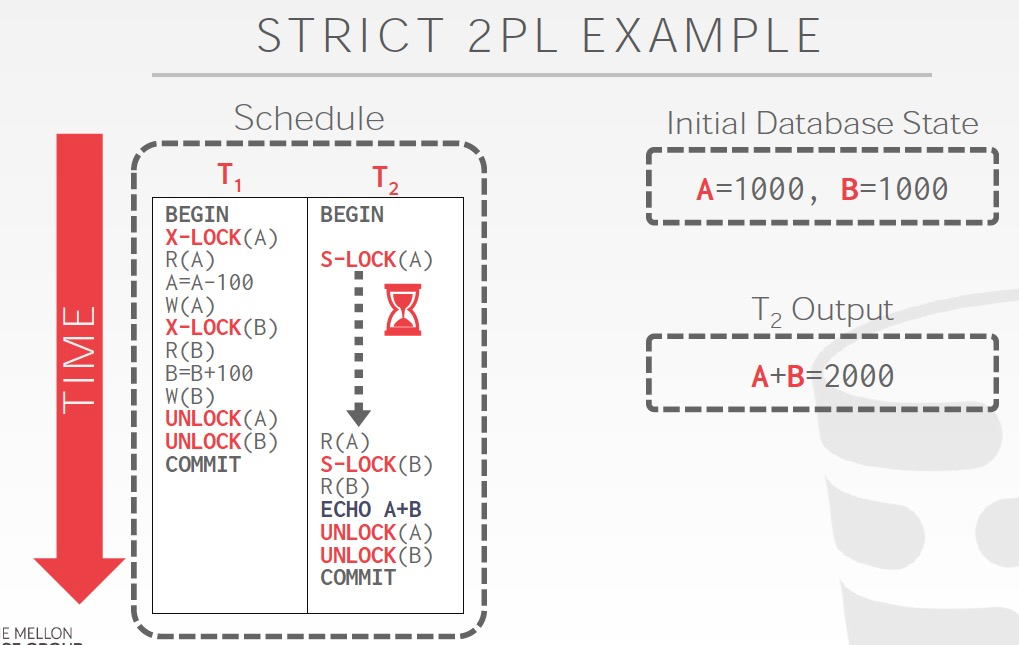
第二，由于脏读导致的Cascding abort，这个的解决很直接，Strict 2PL，Shrinking阶段不会逐步释放锁，最后一起释放，这样就不会脏读了，这个方法会进一步限制并发，谈不上优雅

下面看一组例子，

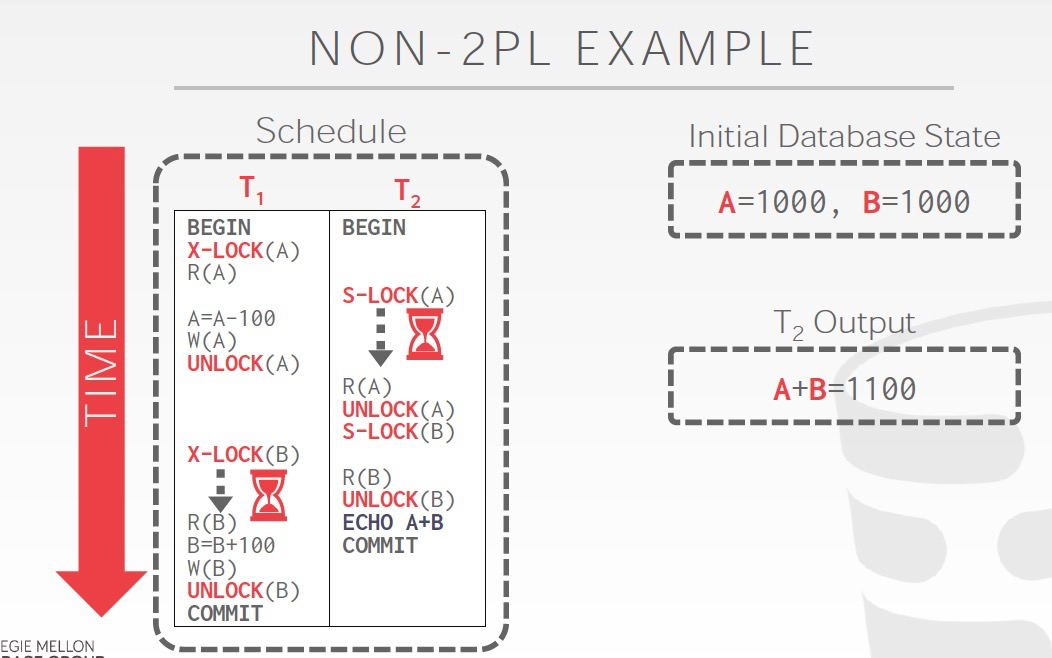
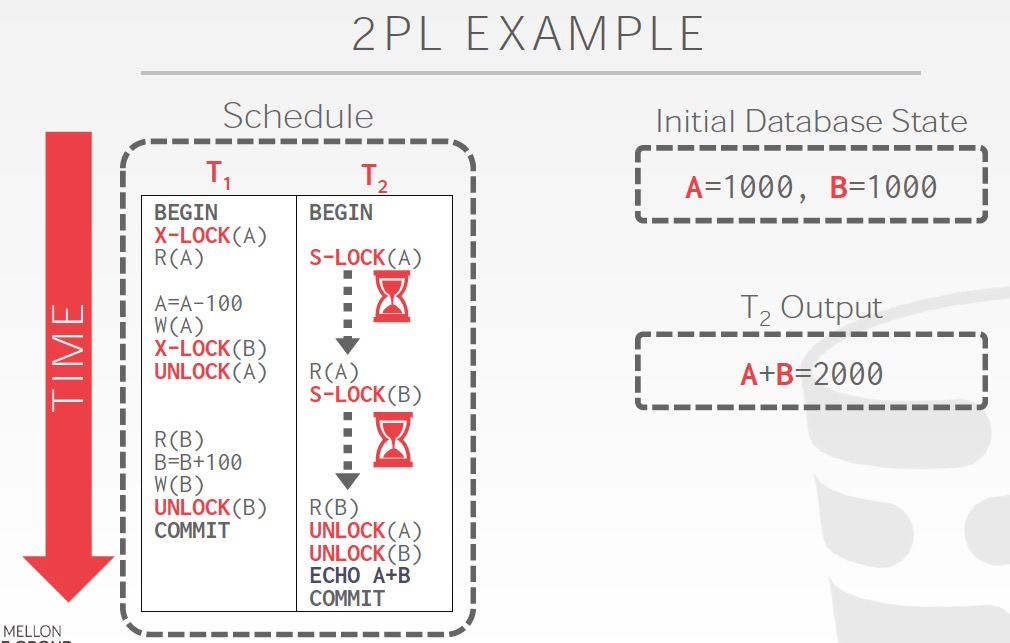
非2PL，读到的是A，B的中间结果，所以会发生不一致；2PL，解决了不一致问题；Strict 2PL，明显进一步限制了并发，几乎就是顺序执行

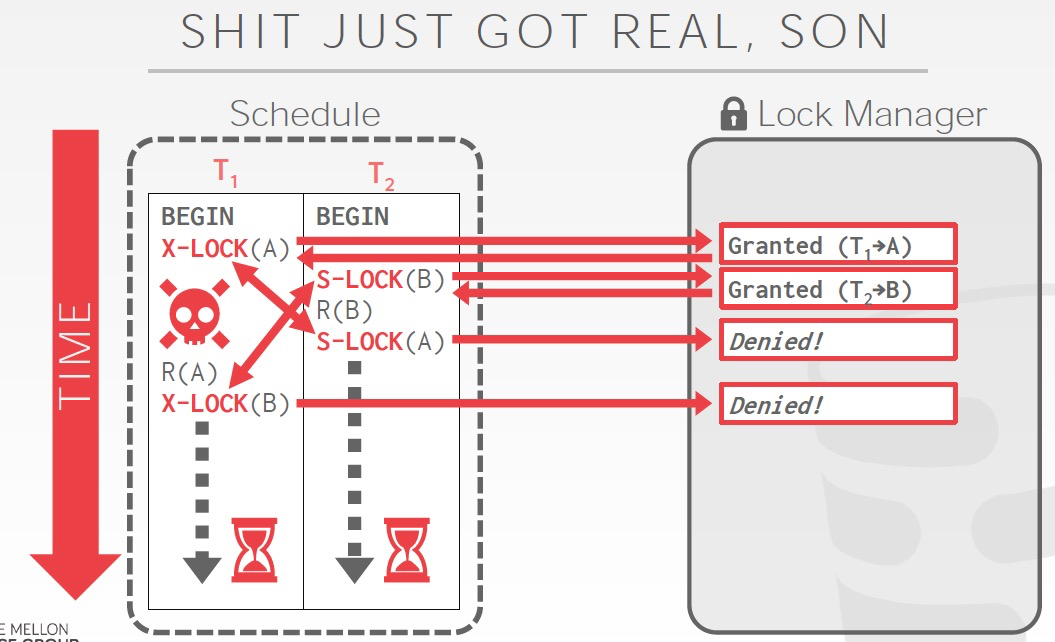
事务还有一个问题，死锁

死锁就是发生锁环了，两种解决方法，

Detection和Prevention，detection就是检测有没有环，如果有环就处理；Prevention就是预先判断是不是会形成环，如果会就拒绝请求

死锁Detection，生成waits-for图，如果有环，就说明有死锁

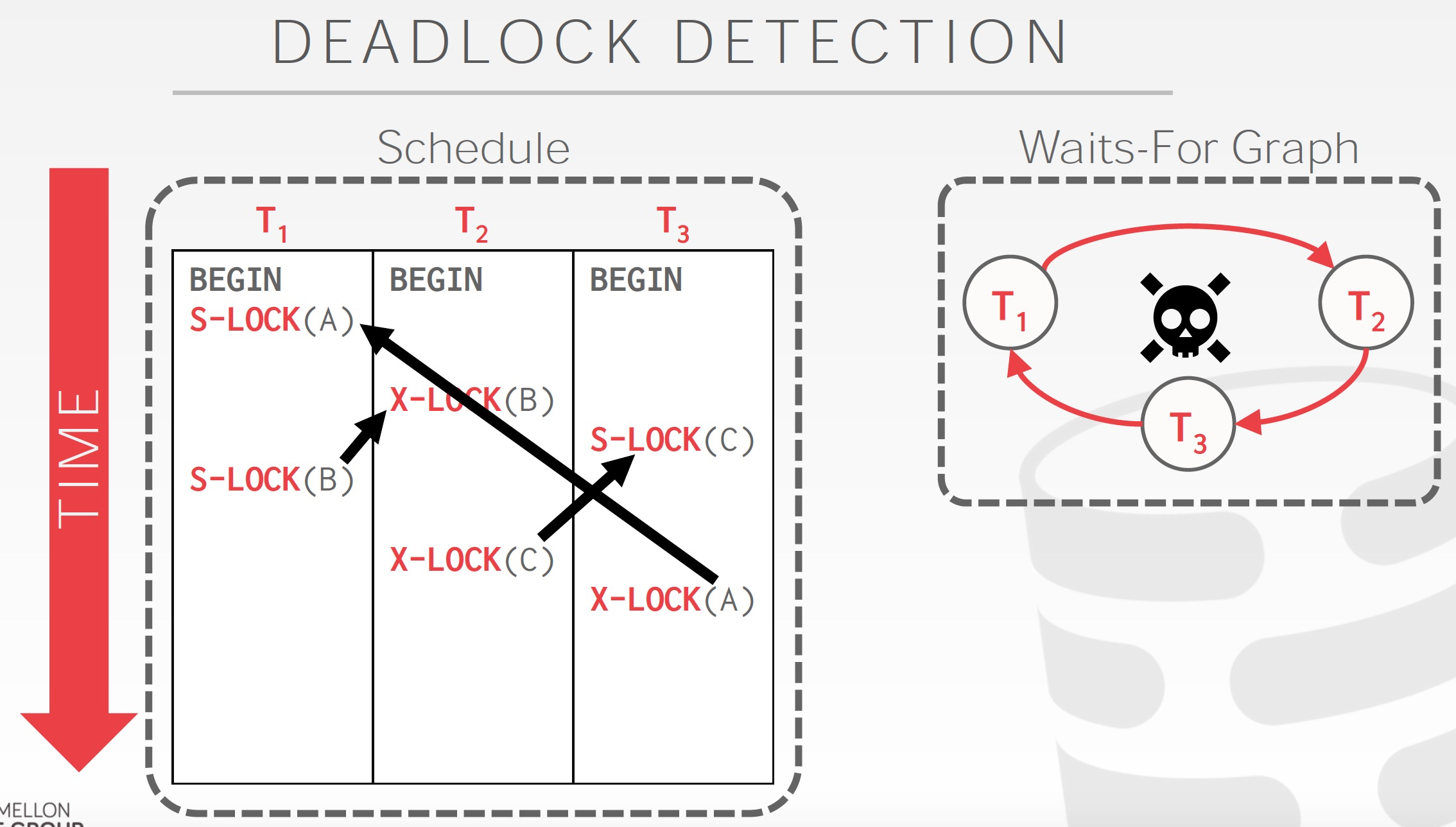
出现死锁，解决从策略就是挑一个进行重启或abort

挑选的策略就是代价更低，然后挑出合适的victim后，就是要进行处理

处理的时候，可以分为完全Rollback和部分Rollback，因为有时候Rollback到不持有这锁就可以解决死锁的问题，不用完全的rollback

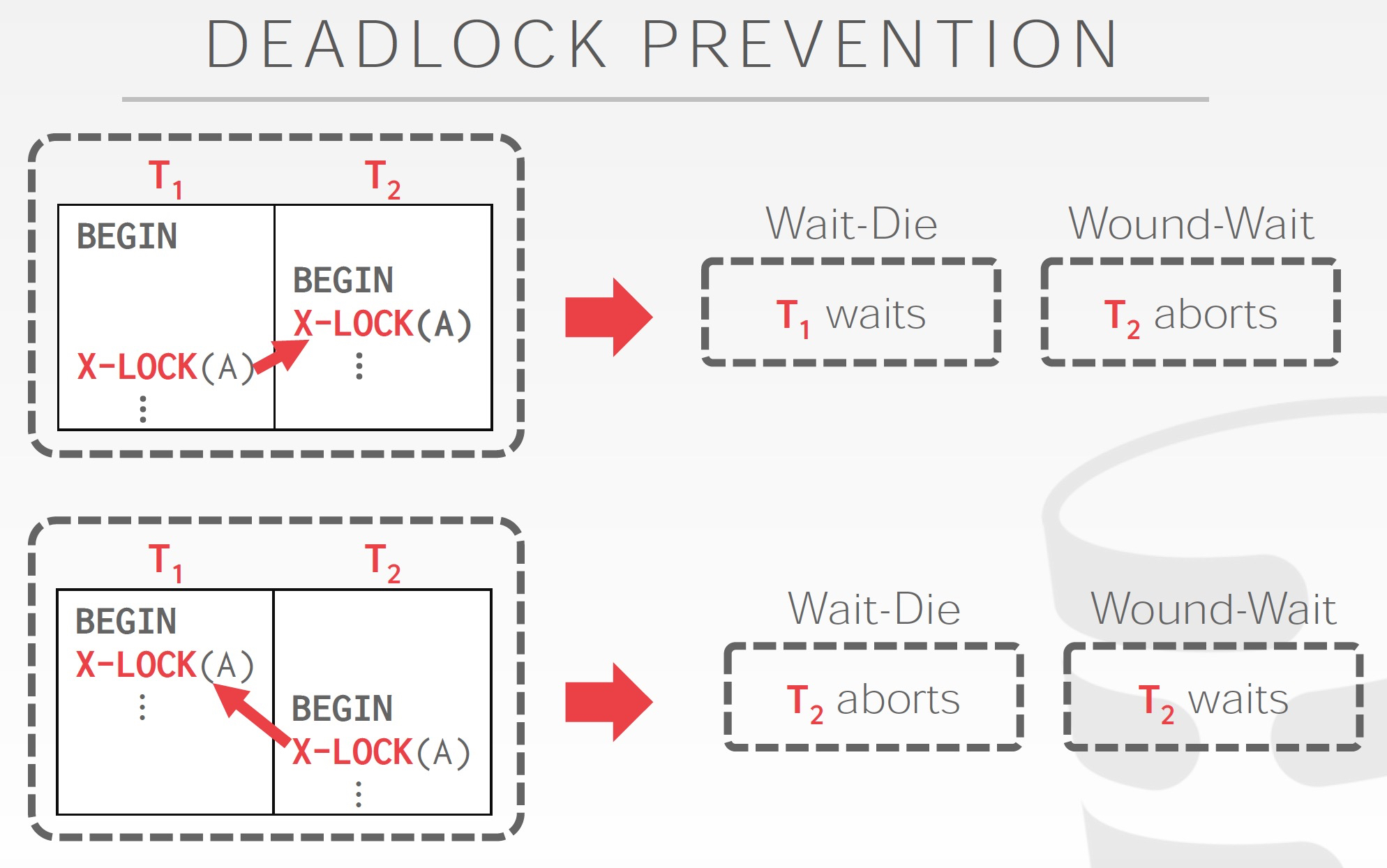
prevention的策略如下，prevention的依据就是时间，要不新的等，要不老的等

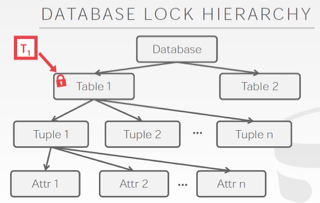
锁粒度

对数据库加锁可以在各个粒度上，

在树上任一节点加锁，意味着对所有子节点也持有锁

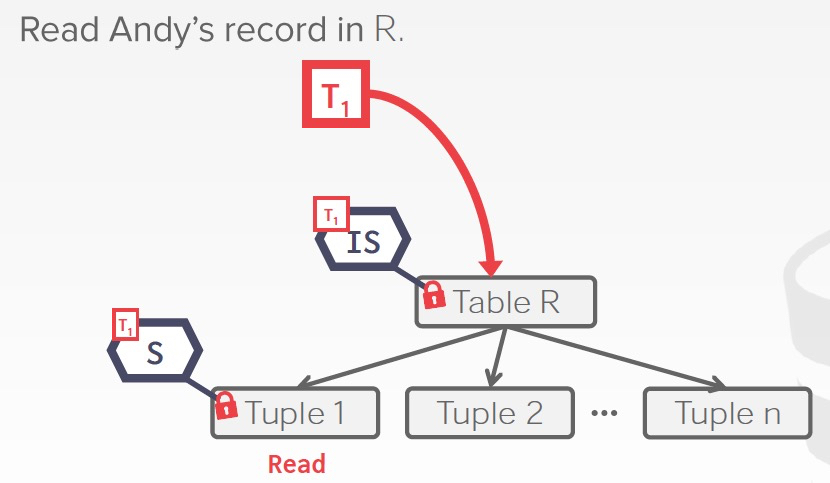
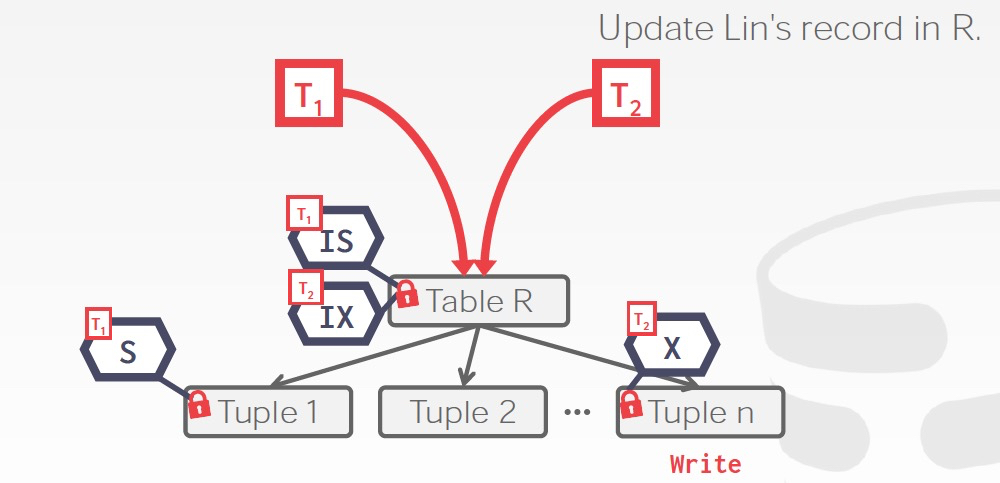
意向锁，intention lock

比如你在要给table加锁的时候，你先要确认table底下的所有tuple，attr是否有锁，这样很低效

所以意向锁就是一个flag，标识子节点上是否有锁

意向锁分为几类，

读写意向锁，很好理解，就是表示子节点是否有读写锁

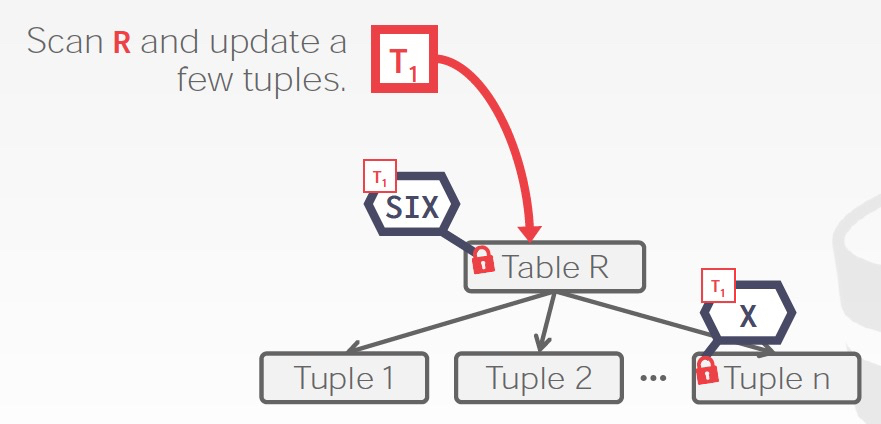
SIX，Shared Intention Exclusive，首先加Shared锁，这样可以扫描全表，然后加IX锁，需要更改其中某些tuple

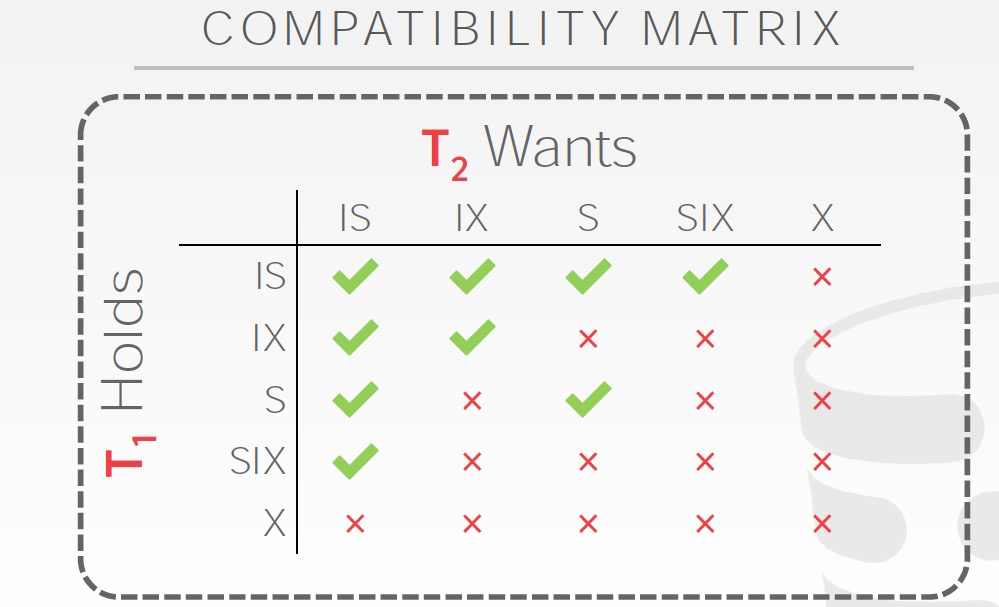
例子，