#NOIP前数学知识总结

我好菜啊……

欧拉函数

欧拉函数φ(n)，是小于n且和n互质的正整数（包括1）的个数。

性质：

1.对于质数n：

$φ(n)=n-1$

2..对于n=p^k

$φ(n)=(p-1)*p^{k-1}$

3.积性函数的性质：

对于互质的m，n，有:

$φ(n*m)=φ(n)*φ(m)$

4.欧拉函数的计算式:

$φ(n)=n*\Pi (1-\frac{1}{p_i})$

5.求小于n且与n互质的数的和：

$S=n*φ(n)/2$

欧拉定理

对于互质的a，m，有:

$a^{\varphi (m)}\equiv 1(mod\  m)$

可以看出费马小定理是欧拉定理的特殊情况。

欧拉定理可以用于指数取模，即$x^y\ \equiv x^{y\ mod\ \varphi (p)}\ (mod\ p)$，p为质数

欧几里得定理

$gcd(a,b)=gcd(b,a\ mod\ b)$

扩展欧几里得

已知a，b，求解一组x，y，使他们满足$ax+by=gcd(a,b)$

证明：

ax+by=gcd(a,b);

1. (1) $a = 0$，$ax+by = gcd(a,b) = gcd(0,b) = b$,

此时$x = 0$(此时x的值是任意的)，$y = 1$；

(2)$b = 0$,$ax + by = gcd(a,b) = gcd(a,0) = a$,

此时$x = 1,y = 0$（此时y的值是任意的）；

2.a和b都不为0时

$ax1 + by1 = gcd(a, b)$

由欧几里德定理：$gcd(a,b) = gcd(b, a\% b)$得

$ax1 + by1 = gcd(a,b) = gcd(b, a\% b)$ 即：

$bx2 + a\% by2 = gcd(b, a\% b) = ax1 + by1$

$a \% b = a - a/b*b$;

$ax1 + by1 = bx2 + (a - a/b*b)y2$;

$=bx2 + ay2 - a/b*b*y2$;

$=ay2 + b(x2-a/b*y2)$;

所以：$x1 = y2,y1 = x2 - a/b*y2$

代码

int exGcd(int a,int b,int &d,int &x,int &y)
{
    if(!b) { d=a;x=;y=; }
    else { gcd(b,a%b,d,y,x); y-= x*(a/b); }
}

求解$ax+by=c$时：

int exgcd(int a,int b,int &x,int &y,int c)
{
    if(!b)
    {
        x=c/a;
        y=;
        return a;
    }
    int g=exgcd(b,a%b,y,x,c);
    y-=a/b*x;
    return g;
}

费马小定理

对于质数p，任意整数a，且a、p互质,有：

$a^p\equiv a(mod\  p)$,即$a^{p-1}\equiv 1(mod\  p)$

乘法逆元

除以一个数再取模等同于乘以这个数的逆元再取模

即

$(a/b)\ mod\ p=(a*inv[b])\ mod\ p$

一个数 x 在模 p 的条件下不一定有逆元, x 关于 p 的逆元存在 当且仅当 x 和 p 互质

求逆元的方法：

1.费马小定理+快速幂

由费马小定理易得 $a*a^{p-2}\equiv 1(mod\  p)$

所以$a^{p-2}$即为所求（要求a、p互质！）

2.线性推逆元

求1!~n!的逆元：

$inv[i] =inv[i+1]*(i+1) (mod\ p)$

inline void get_finv()
{
    fac[]=finv[]=;
    for(int i=;i<=n;++i;++i)
        fac[i]=fac[i-]*i%mod;
    finv[n]=quick_pow(fac[n],mod-);
    for(int i=n-;i;--i)
        finv[i]=finv[i+]*(i+)%mod;
}

证明：

 fac[i] * inv[i] ≡1 (mod p)
 fac[i+1] * inv[i+1] ≡1 (mod p) =>  fac[i]* (i+1) * inv[i+1] ≡1(mod p)
 由 同余的除法原理可得 :  inv[i] ≡inv[i+1] * (i+1)
 推导完毕

求1~n的逆元：

$inv[i]=inv[p\ mod\ i] * (- p/i) (mod\ p)$

inline void get_inv()
{
    inv[]=inv[]=;
    for(int i=;i<=n;++i)
        inv[i]=inv[mod%i]*(mod-mod/i)%mod;
}

证明：

  令 s = p/i , t = p%i , 则有： s*i + t = p  (显然)
    然后 s*i + t ≡ 0 (mod p)
    移项得  t ≡ -s*i (mod p)
    同除以 t * i 得  t / (t*i) ≡ -s*i / (t*i) (mod p)
    将除法转化为乘法 => inv[i] ≡ -s * inv[t] (mod p)
    于是将 s=p/i , t=p%i带入就可以得到:  inv[i] ≡ inv[p%i] * (-p/i) (mod p)
    推导完毕

3.扩展欧几里得

$axΞ1(mod\ b)$

-->$ax+by=1$

利用扩欧求解

//转载 from Judge
#define ll long long
const int mod=; //同上
 void ex_gcd(ll a,ll b,ll &x,ll &y){
    if(!b){ x=,y=; return ; }
    ex_gcd(b,a%b,x,y);
    ll t=x; x=y,y=t-(a/b)*y;
 }
 //当然你也可以这么写,更能体现公式:
 //  ll X=x,Y=y;
 //  x=Y,y=X-(a/b)*Y;
 inline ll inv(ll a){
    ll inv_a,y;
    ex_gcd(a,mod,inv_a,y);
    return inv_a;
 }

中国剩余定理

求解同余方程组

xΞa₁(mod m₁)

xΞa₂(mod m₂)

xΞa₃(mod m₃)

......

xΞa_k(mod m_k)

其中a₁ a₂ a₃... a_k两两互质

求x的最小非负整数解

定理内容

令$M=lcm(m_1,m_2,m_3,...m_k)$,即$M=m_1*m_2*m_3*...*m_k$

$t_i$为 $\frac{M}{m_i} t_i \equiv 1\ (mod\ m_i)$的最小非负整数解

则必有一解为

$x=\sum \limits _{i=1}^{k} a_i \frac{M}{m_i} t_i$

通解为$x+i×M$

最小非负整数解为$(M+x\ mod\ M)\ mod\ M$

//ti​同余式的求解可以用扩展欧几里得

void exgcd(int a,int b,int &x,int &y)
{
    if(b==){ x=; y=; return;}
    exgcd(b,a%b,x,y);
    int tp=x;
    x=y; y=tp-a/b*y;
}

int china()
{
    int ans=,lcm=,x,y;
    for(int i=;i<=k;++i) lcm*=b[i];
    for(int i=;i<=k;++i)
    {
        int tp=lcm/b[i];
        exgcd(tp,b[i],x,y);
        x=(x%b[i]+b[i])%b[i];//x要为最小非负整数解
        ans=(ans+tp*x*a[i])%lcm;
    }
    return (ans+lcm)%lcm;
}

扩展中国剩余定理

用于解决m₁，m₂，m₃...m_n不互质的情况。

考虑只有m₁,m₂的情况：

设解为x

可得

$x=a_1+k_1*m_1 ; x=a_2+k_2*m_2$

$a_1+k_1*m_1 = a_2+k_2*m_2$

$k_2*m_2-k_1*m_1=a_1-a_2$

形式与扩欧可解的同余方程十分相似

设g=gcd(m₁,m₂)

若$a_1-a_2$不是g的倍数 就无解辽（详见exgcd解同余方程有解的条件）

否则解这个同余方程

最终的解$\times \frac{c}{g}$可得$k_1$

由$x=-k_1\times m_1+a_1$解得x

则通解$X=x+k\times lcm(m_1,m_2)$

最终得到$x=x_0 (mod lcm(m_1,m_2))$

以此类推，解n次扩欧得到最终解。

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=;
int n;
ll m[N],a[N];
ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if(!b)
    {
        x=;y=;
        return a;
    }

    ll gcd=exgcd(b,a%b,y,x);
    y-=(a/b)*x;
    return gcd;
}

ll excrt()
{
    ll x,y,lcm=m[],ans=a[],gcd;
    for(int i=;i<=n;i++)
    {
        gcd=exgcd(lcm,m[i],x,y);
        if((ans-a[i])%gcd)return -;
        x=(ans-a[i])/gcd*x%m[i];
        ans-=lcm*x;
        lcm=lcm/gcd*m[i];
        ans%=lcm;
    }
    return (ans%lcm+lcm)%lcm;
}
void work()
{
    for(int i=;i<=n;i++)
        scanf("%lld%lld",&m[i],&a[i]);
    cout<<excrt()<<endl;
}
int main()
{
    while(scanf("%d",&n)==)work();
    return ;
}

排列组合

排列数

从n个不同元素中取出m个元素(m<=n)的所有不同排列的个数。

$A_n^m=n(n-1)(n-2)\cdots(n-m+1)=\frac{n!}{(n-m)!},\quad n,m\in \mathbb{N}^* ,\text{并且}m\leq n$

特别地，规定0!=1.

组合数

从n个不同元素中取出m个元素(m<=n)的所有不同组合的个数。

$C_n^m=\frac{A_n^m}{A_m^m}=\frac{n(n-1)(n-2)\cdots (n-m+1)}{m!}=\frac{n!}{m!(n-m)!},\quad n,m\in \mathbb{N}^* ,\text{并且}m\leq n$

规定$C_n^0=C_n^n=1$

二项式定理

常见形式

$(x+1)^n=\sum_{i=0}^{n} C(n,i) ~ x^i$

证明：

(x+1)ⁿ=(x+1)*(x+1)*...*(x+1)

从这n个(x+1)中选择n次，每次只可能选出x或1。

那么答案即为每次选出n个元素相乘后将结果累加

而从n个(x+1)中选出i个x的情况数即为

^{$C_n^i$}

证毕。

Lucas定理

定理内容

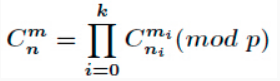
证明

(咕咕咕)

代码

ll C(ll x,ll y,ll mod)
{
    if(x<y)return ;
    return fac[x]*qpow(fac[y],p-,p)%p*qpow(fac[x-y],p-,p)%p;
}
ll lucas(ll x,ll y,ll p)
{
    if(!y)return ;
    return C(x%p,y%p,p)*lucas(x/p,y/p,p)%p;
}

莫比乌斯反演(强行NOIP前)

两类基本形式：

$\begin{aligned} &(1).F(n)=\sum_{d|n}f(d)\Rightarrow f(n)=\sum_{d|n}\mu(d)F(\frac{n}{d})&\\ &(2).F(n)=\sum_{n|d}f(d)\Rightarrow f(n)=\sum_{n|d}\mu(\frac{d}{n})F(n)(最常用)&\\ \end{aligned}$

范德蒙恒等式

$\sum_{i=0}^{k} C_n^i C_m^{k-i}=C_{n+m}^k$

φ(n)=n−1