POJ3087 Shuffle'm Up —— 打表找规律 / map判重

题目链接：http://poj.org/problem?id=3087

Shuffle'm Up

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 12305		Accepted: 5708

Description

A common pastime for poker players at a poker table is to shuffle stacks of chips. Shuffling chips is performed by starting with two stacks of poker chips, S₁ and S₂, each stack containing C chips.
Each stack may contain chips of several different colors.

The actual shuffle operation is performed by interleaving a chip from S₁ with a chip from S₂ as shown below for C = 5:

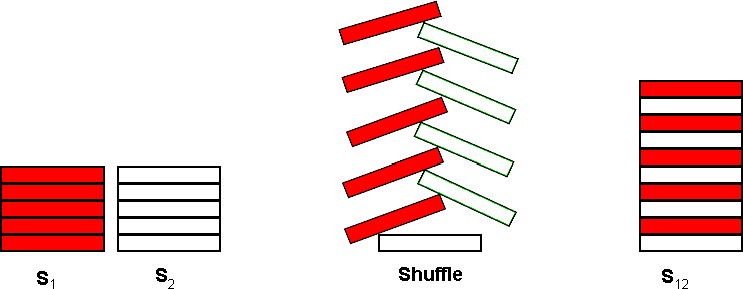
The single resultant stack, S₁₂, contains 2 * C chips. The bottommost chip of S₁₂ is the bottommost chip from S₂. On top of that chip, is the bottommost
chip from S₁. The interleaving process continues taking the 2^nd chip from the bottom of S₂ and placing that on S₁₂, followed by the 2^nd chip from the
bottom of S₁ and so on until the topmost chip from S₁ is placed on top of S₁₂.

After the shuffle operation, S₁₂ is split into 2 new stacks by taking the bottommost C chips from S₁₂ to form a new S₁ and the topmost C chips
from S₁₂ to form a new S₂. The shuffle operation may then be repeated to form a new S₁₂.

For this problem, you will write a program to determine if a particular resultant stack S₁₂ can be formed by shuffling two stacks some number of times.

Input

The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the number of datasets that follow.

Each dataset consists of four lines of input. The first line of a dataset specifies an integer C, (1 ≤ C ≤ 100) which is the number of chips in each initial stack (S₁ and S₂).
The second line of each dataset specifies the colors of each of the C chips in stack S₁, starting with the bottommost chip. The third line of each dataset specifies the colors of each of the C chips
in stack S₂ starting with the bottommost chip. Colors are expressed as a single uppercase letter (A through H). There are no blanks or separators between the chip colors. The fourth line of each
dataset contains 2 * C uppercase letters (A through H), representing the colors of the desired result of the shuffling of S₁ and S₂ zero or
more times. The bottommost chip’s color is specified first.

Output

Output for each dataset consists of a single line that displays the dataset number (1 though N), a space, and an integer value which is the minimum number of shuffle operations required to get the desired resultant stack. If the
desired result can not be reached using the input for the dataset, display the value negative 1 (−1) for the number of shuffle operations.

Sample Input

2
4
AHAH
HAHA
HHAAAAHH
3
CDE
CDE
EEDDCC

Sample Output

1 2
2 -1

Source

Greater New York 2006

题解：

方法一：经打表发现，当经过2n次洗牌之后，必定能回到初始状态，所以直接枚举到2n。 问：为何经过2*n后必定能回到初始状态？自己也不会证明，但有一点：对于一个数来说，它所在的位置只有2n种情况。应该与这个有关。复杂度计算：1000（测试组数）*200（2n）*200（字符串长度） = 4e7，如果真的是这个计算次数的话，是会超时的，但可能数据比较弱。

方法二：直接模拟，然后加个map判重，如果某个状态出现过，并且不是目标状态，则可以得出结论：不可能得到目标状态。因为洗牌的状态是会不断循环的，当发现一个状态已经出现过，则表明之前的那些状态构成一个循环，同时也是所有状态的集合，所以不可能得到目标状态。复杂度计算：1000（测试组数）*200（2n）*log200（map判重）*200（字符串长度） = 4e7 * log200， 跟方法一差不了多少（log200很小了）。

代码一：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 #define ms(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = +;

 char a[MAXN], b[MAXN], c[MAXN], aim[MAXN];

 int main()
 {
     int T, n;
     scanf("%d",&T);
     for(int kase = ; kase<=T; kase++)
     {
         scanf("%d",&n);
         scanf("%s%s%s", a, b, aim);
         int ans = -;
         for(int k = ; k<=*n; k++)
         {
             int cnt = ;
             for(int i = ; i<n; i++)
             {
                 c[cnt++] = b[i];
                 c[cnt++] = a[i];
             }
             c[cnt] = '\0';
             if(strcmp(c, aim)==)
             {
                 ans = k;
                 break;
             }
             for(int i = ; i<n; i++)
             {
                 a[i] = c[i];
                 b[i] = c[n+i];
             }
         }
         printf("%d %d\n",kase, ans);
     }
 }

代码二：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 #define ms(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = +;

 char a[MAXN], b[MAXN], c[MAXN], aim[MAXN];
 map<string, bool>exist;

 int main()
 {
     int T, n;
     scanf("%d",&T);
     for(int kase = ; kase<=T; kase++)
     {
         scanf("%d",&n);
         scanf("%s%s%s", a, b, aim);
         exist.clear();
         int ans;
         for(int k = ; true; k++)
         {
             int cnt = ;
             for(int i = ; i<n; i++)
             {
                 c[cnt++] = b[i];
                 c[cnt++] = a[i];
             }
             c[cnt] = '\0';
             if(strcmp(c, aim)==)
             {
                 ans = k;
                 break;
             }
             else if(exist[c])
             {
                 ans = -;
                 break;
             }
             exist[c] = true;
             for(int i = ; i<n; i++)
             {
                 a[i] = c[i];
                 b[i] = c[n+i];
             }
         }
         printf("%d %d\n",kase, ans);
     }
 }