【算法】最长回文子串 longest palindrome substring

对于字符串S， 要找到它最长的回文子串，能想到的最暴力方法，应该是对于每个元素i-th都向左向右对称搜索，最后用一个数组span 记录下相对应元素i-th为中心的回文子串长度。

那么问题来了：

　　1. 这样的方法，对于奇回文子串和偶回文子串的处理不一样，比如所“acbca” 和“acbbca”

　　2. 计算冗余，e.g. ”sscssabcccchccccba“中， 自左向右遍历计算的话，会发现， ”abcccchccccba“是对称的，而这个回文字符串里又左右对称分别包含了两个回文子字符”cccc“和”cccc“， 在对第二个”cccc“字符串遍历的时候，其实可以利用到”abcccchccccba“的对称性来直接赋值，而不用再次计算

于是，引出了Manacher's 算法：

　　1. 为了可以对奇偶回文字符串不加区分地处理，对输入字符串增加边界元素（输入字符串S长度为N -> S2长度为2*N+1）：e.g. ”aabbbcc“ -> "#a#a#b#b#b#c#c#" ， ”aabbcc“ -> "#a#a#b#b#c#c#"

　　2. 对于S2字符串，自左向右，每个字符逐个计算和处理

　　　　1）用span[maxInputStringLength*2+1]数组来记录每个元素i-th为中心的回文字符串长度 ： 初始化 span[0] = 0

　　　　2）用center 和 rightBoundary 来记录上一个已知的回文字符串中心index和最右边界index ：初始化 center = 0， rightBoundary = 0

　　　　3）用 i 表示当前处理的元素， i2 表示 以 center 为中心的 center左侧 i 对称 元素下标 ： i2 = center - （i - center）= center * 2 - i

　　　　4）加上已知的回文子串信息之后，假设已经处理了S2[0, i-1]范围的元素，那么已知的回文子串中心center 必然属于[0, i-1]区间， 但是对于rightBoundary和i的关系可以有三种情况：

　　　　　　a）当前处理的元素（index = i）以 center为中心，对称的元素（index = i2）上有，span[i2] < rightBoundary - i - 1， 表示i2点的回文字符串最左端不会超过leftBoundary的长度，利用了已知的回文字符串信息辅助说明，当前以i为中心的回文字符串将和i2完全对称，span[i] = span[i2]

　　　　　　

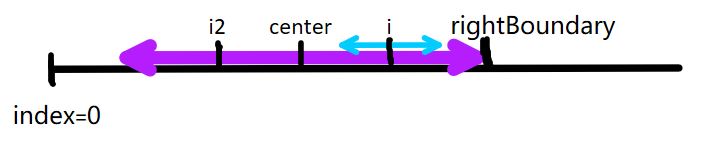
　　　　　　b）当前处理的元素（index = i）以 center为中心，对称的元素（index = i2）上有，span[i2] >= rightBoundary - i - 1, 表示 i2 点的回文字符串最左端已经超过了leftBoundary的范围，不能利用已知回文字符串直接赋值，但还是可以利用对称性，使得对称搜索从rightBoundary处开始，这样可以减少计算

　　　　　　

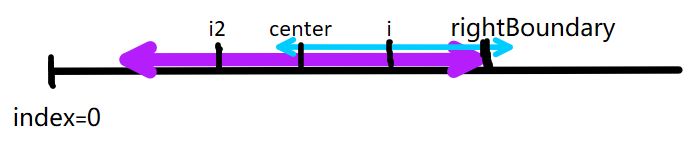
　　　　　　c）当前处理的元素（index = i）并不在已知回文串的记录范文内，那么久没有辅助信息，需要从i元素的左右对称搜索，得到span[i]的值

　　　　　　

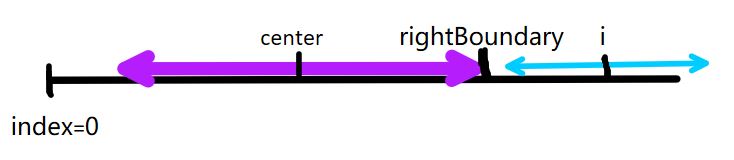
　　　　5）最后要更新center和rightBoundary的值，使得已知回文字符串的覆盖范围右移，这样可以持续辅助搜索

　　

 const int maxStringLength = ;

 string longestPalindrome(string s) {

     if (s.empty()) return "";

     ///add boundary
     string s2;
     for (int i = ; i < s.size(); i++) {
         s2.push_back('#');
         s2.push_back(s[i]);
     }
     s2.push_back('#');

     /// setting
     int span[maxStringLength] = {};
     span[] = ; // init the first element's length of palindrome
     int center = , rightBoundary = ;
     int left = , right = ;

     ///traverse
     for (int i = ; i < s2.size(); i++) {
         if (i <= rightBoundary) {
             int i2 = center *  - i;// center - (i - center)
             if (span[i2] < (rightBoundary - i - )) {
                 span[i] = span[i2];
                 left = -;
             }
             else {
                 span[i] = rightBoundary - i;
                 right = rightBoundary + ;
                 left = i *  - right; //i - (right - i)
             }
         }
         else {
             span[i] = ;
             left = i - ;
             right = i + ;
         }

         while (left >=  && right < s2.size() && s2[left] == s2[right]) {
             span[i] ++;
             left--;
             right++;
         }

         if ((i + span[i]) > rightBoundary) {
             center = i;
             rightBoundary = i + span[i];
         }
     }

     /// find the max span length
     int maxSubstringCenter = , maxSubstringLen = ;
     for (int i = ; i < s2.size(); i++) {
         if (span[i] > maxSubstringLen) {
             maxSubstringLen = span[i];
             maxSubstringCenter = i;
         }
     }

     /// remove boundary '#' from substring
     string result;
     for (int i = maxSubstringCenter - maxSubstringLen; i <= maxSubstringCenter + maxSubstringLen; i++) {
         if (s2[i] != '#')
             result.push_back(s2[i]);
     }

     return result;
 }