CH0601 Genius ACM【倍增】【归并排序】

0601 Genius ACM 0x00「基本算法」例题

描述

给定一个整数 M，对于任意一个整数集合 S，定义“校验值”如下:

从集合 S 中取出 M 对数(即 2∗M 个数，不能重复使用集合中的数，如果 S 中的整 数不够 M 对，则取到不能取为止)，使得“每对数的差的平方”之和最大，这个最大值 就称为集合 S 的“校验值”。

现在给定一个长度为 N 的数列 A 以及一个整数 T。我们要把 A 分成若干段，使得 每一段的“校验值”都不超过 T。求最少需要分成几段。

Advanced CPU Manufacturer (ACM) is one of the best CPU manufacturer in the world. Every day, they manufacture n CPU chips and sell them all over the world.

As you may know, each batch of CPU chips must pass a quality test by the QC department before they can be sold. The testing procedure is as follows:

1) Randomly pick m pairs of CPU chips from the batch of chips (If there are less than 2m CPU chips in the batch of chips, pick as many pairs as possible.)

2) For each pair, measure the Relative Performance Difference (RPD) between the two CPU chips. Let Di be the RPD of the i-th pair

3) Calculate the Sqared Performance Difference (SPD) of the batch according to the following formula:

SPD=∑Di2

If there are only 1 CPU in a batch, then the SPD of that batch is 0.

4) The batch of chips pass the test if and only if SPD≤k, where k is a preseted constant

Usually they send all the n CPU chips as a single batch to the QC department every day. As one of the best CPU manufacturer in the world, ACM never fail the test. However, with the continuous improvement of CPU performance, they find that they are at risk!

Of course they don't want to take any risks. So they make a decision to divide the n chips into several batches to ensure all of them pass the test. What’s more, each batch should be a continuous subsequence of their productions, otherwise the QC department will notice that they are cheating. Quality tests need time and money, so they want to minimize the number of batches.

Given the absolute performance of the n chips P1 ... Pn mesured by ACM in order of manufacture, your task is to determine the minimum number of batches to ensure that all chips pass the test. The RPD of two CPU chips equals to the difference of their absolute performance.

输入格式

The first line contains a single integer T, indicating the number of test cases.

In each test case, the first line contains three integers n, m, k. The second line contains n integers, P1 ... Pn.

输出格式

For each test case, print the answer in a single line.

样例输入

2
5 1 49
8 2 1 7 9
5 1 64
8 2 1 7 9

样例输出

2
1

数据范围与约定

• T≤12
  1≤n,m≤5×105
  0≤k≤1018
  0≤Pi≤220

来源

沈洋，ACM-ICPC Beijing 2016

Contest Hunter - 信息学自助比赛平台

思路：

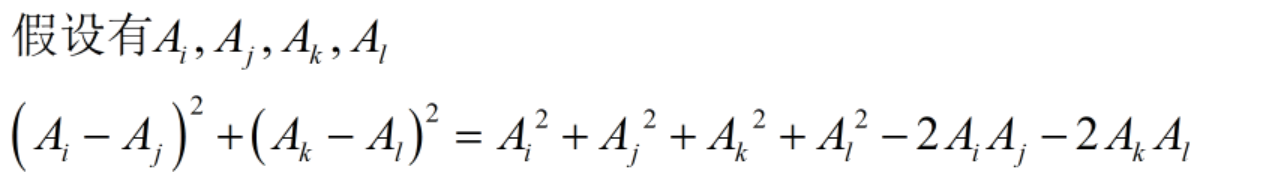不论Ai,Aj,Ak,Al的相对大小如何，的大小不变。因此要使得该式最大，应使4个数中最大的那一个数之前的系数最小。也就是说，最大的和最小的相配，次大的和次小的相配。

为了让分段的段数最少，我们应该要尽量让每一段都在不超过k的前提下尽量多的包含数。

那么我们从头开始对A进行分段，让每一段尽量长，到结尾时就可以得到答案。

所以我们枚举每一段的开头，去找右端点。求校验值时需要对一段进行排序。如果二分右端点R，R可能只会扩展一点点，浪费很多时间。

用倍增求右端点会比较好：

1.初始化p=1,R = L

2.求出[L, R + p]区间的校验值，若校验值<= k， 则R+=p,p*=2,否则p/=2

3.重复，直到p=0,R即为右端点

如果单纯只使用sort，还是会T，因为我们每次倍增时，有一部分的数已经有序了。所以可以运用归并排序的思想。将已经有序的序列和新扩展的序列合并，会大大缩短时间。

虐狗宝典学习笔记：

我们在进行递推时，如果状态空间很大，通常的线性递推无法满足时间与空间复杂度的要求，那么我们可以通过成倍增长的方式，只递推状态空间中在2的整数次幂位置上的值作为代表。当需要其他位置上的值时，我们通过“任意整数可以表示成若干个2的次幂项的和”这一性质，使用之前求出的代表值拼成所需的值。

 #include <iostream>
 #include <set>
 #include <cmath>
 #include <stdio.h>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 typedef long long LL;

 LL m, n, t, k;
 const int maxn = 5e5 + ;
 LL s[maxn], b[maxn], c[maxn];

 bool check(LL l, LL r, LL lr)
 {
     LL tot = ;
     int t = l, len = r - l + ;
     for(LL i = lr; i <= r; i++){
         b[i] = s[i];
     }
     sort(b + lr, b + r + );
     if(l == lr){
         for(int i = l; l <= r; i++){
             c[i] = b[i];
         }
     }
     else{
         int i = l, j = lr;
         while(i < lr && j <= r){
             if(b[i] <= b[j]){
                 c[t++] = b[i++];
             }
             else{
                 c[t++] = b[j++];
             }
         }
         while(i < lr)c[t++] = b[i++];
         while(j <= r)c[t++] = b[j++];
     }
     LL jiaoyan = ;
     for(LL i = l; i <= min(l + m - , l + (r - l + ) /  - ); i++){
         jiaoyan += (c[r - i + l] - c[i]) * (c[r - i + l] - c[i]);
     }
     if(jiaoyan <= k){
         for(int i = l; i <= r; i++){
             b[i] = c[i];
         }
         return ;
     }
     return ;
 }

 int main()
 {
     scanf("%lld", &t);
     while(t--){
         scanf("%lld%lld%lld", &n, &m, &k);
         for(LL i = ; i <= n; i++){
             scanf("%lld", &s[i]);
         }

         memset(b, , sizeof(b));
         memset(c, , sizeof(c));
         LL sum = , l = , r = , p = ;
         b[] = s[];
         while(r < n){
             if(!p){
                 sum++;
                 p = ;r++;
                 l = r;
                 b[l] = s[l];
                 continue;
             }
             if(p){
                 if(r + p <= n && check(l, r + p, r + )){
                     r += p;
                     p *= ;
                     if(r == n)break;
                 }
                 else{
                     p /= ;
                 }
             }
             //cout<<sum<<endl;

         }
         if(r == n)sum++;

         printf("%lld\n", sum);
     }
 }