【[HNOI2008]GT考试】

我又来复习\(kmp\)了

其实这道题主要是一个矩阵乘法，但是\(kmp\)在其中也有着非常重要的作用

我们可以这样定义状态\(dp[i][j]\)表示文本串进行到了\(i\)位置，同时文本串在最后和模式串匹配了一共\(j\)位的方案数

于是答案就是\(\sum_{i=0}^{m-1}dp[n][i]\)

之后我们想一下转移

显然\(dp[i]\)需要从\(i-1\)转移过来

但是怎么转移呢

有一个非常直观也非常\(sb\)的想法就是直接\(dp[i][j]=dp[i-1][j-1]\)

毕竟再补上模式串的第\(j\)位就可以啦

但是转移不止这些

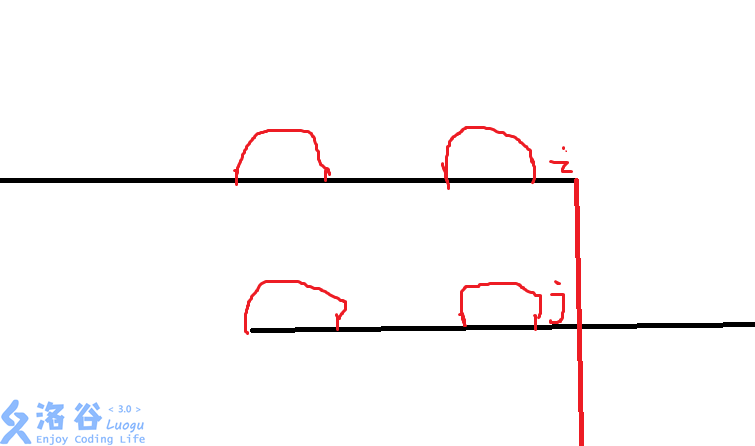
那四个画出来的部分是\(next[j]\)

如果我们在转移\(dp[i][j]\)的状态的时候并不让文本串的第\(i\)位和模式串的第\(j\)位相等，而是在这里填上模式串的\(next[j]\)位置上的数

那么很显然\(dp[i-1][nx[j]]+=dp[i-1][j-1]\)

所以我们用\(kmp\)预处理出来一个这样的数组\(a[i][j]\)表示匹配到在模式串上匹配\(j\)向\(i\)转移的时候可以填几个数字

所以现在就有

\[dp[i][j]=\sum_{k=0}^{m-1}dp[i-1][k]*a[i][k]
\]

显然这是一个矩阵乘法就可以优化的柿子

现在的问题就变成了\(a\)数组怎么求

首先求出\(next\)数组，之后枚举这一位填什么，之后往前跳\(nx\)，直到匹配就好了

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define maxn 21
int dp[1001][maxn];
char S[maxn];
int n,m,mod;
int nx[maxn];
int ans[maxn][maxn];
int a[maxn][maxn];
inline void did_a()
{
	int mid[maxn][maxn];
	for(re int i=0;i<m;i++)
		for(re int j=0;j<m;j++)
			mid[i][j]=a[i][j],a[i][j]=0;
	for(re int i=0;i<m;i++)
		for(re int j=0;j<m;j++)
			for(re int k=0;k<m;k++)
			{
				a[i][j]+=mid[i][k]*mid[k][j];
				if(a[i][j]>=mod) a[i][j]%=mod;
			}
}
inline void did_ans()
{
	int mid[maxn][maxn];
	for(re int i=0;i<m;i++)
		for(re int j=0;j<m;j++)
			mid[i][j]=ans[i][j],ans[i][j]=0;
	for(re int i=0;i<m;i++)
		for(re int j=0;j<m;j++)
			for(re int k=0;k<m;k++)
			{
				ans[i][j]+=mid[i][k]*a[k][j];
				if(ans[i][j]>=mod) ans[i][j]%=mod;
			}
}
inline void quick(int b)
{
	while(b)
	{
		if(b&1) did_ans();
		b>>=1;
		did_a();
	}
}
int main()
{
	scanf("%d%d%d",&n,&m,&mod);
	scanf("%s",S+1);
	nx[0]=nx[1]=0;
	for(re int i=2;i<=m;i++)
	{
		int p=nx[i-1];
		while(p&&S[p+1]!=S[i]) p=nx[p];
		if(S[p+1]==S[i]) nx[i]=++p;
			else nx[i]=0;
	}
	for(re int i=0;i<m;i++)
		for(re char j='0';j<='9';j++)
		{
			int p=i;
			while(p&&S[p+1]!=j) p=nx[p];
			if(S[p+1]==j) a[p+1][i]++;
			else a[0][i]++;
		}
	for(re int i=0;i<m;i++) ans[i][i]=1;
	quick(n);
	int tot=0;
	for(re int i=0;i<m;i++)
		tot=(tot+ans[i][0])%mod;
	std::cout<<tot;
	return 0;
}