3D游戏与计算机图形学中的数学方法-变换
1变换
在3D游戏的整个开发过程中,通常需要以某种方式对一系列的向量进行变换。通常用到的变换包括平移,缩放和旋转。
1.1通用变换
通常可将n x n可逆矩阵M看成是一个从坐标系到另一个坐标系的变换矩阵。M的列给出了坐标系从原坐标系到新坐标系的映射。例如M是一个n x n可逆矩阵,当M与向量(1,0,0),(0,1,0)和(0,0,1)相乘时,可以得到
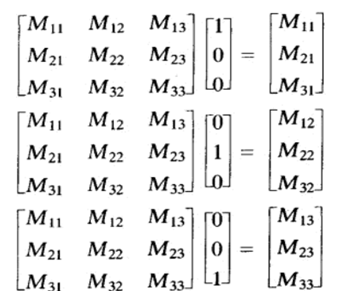
类似地,M-1的列给出了坐标轴从新坐标轴系到原坐标轴系的映射。这样对于任意给定的线性无关的向量U,V,W可以构造一个变换矩阵,该矩阵将这些向量映射到向量(1,0,0),(0,1,0)和(0,0,1)。
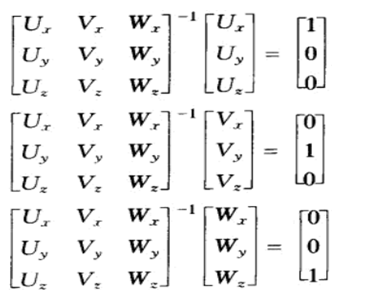
多个变换可以串联起来,并且可以将多个变换矩阵的乘积用一个矩阵来表示。假设需要先用矩阵M后用矩阵G对一个对象进行变换,由于乘积满足结合律,对于任意向量P都有G(MP)=(GM)P,因此只需存储GM的乘积得到的矩阵,将该矩阵作为对象的变换矩阵即可。这样就可以对定点进行多次变换,而存储空间不变。
正交矩阵是一种其转置矩阵等于其逆矩阵的矩阵。正交矩阵只能用于表示旋转和反射的组合。
反射指在某一方向上将点进行镜像的一种运算。例如,矩阵
 以xy平面为对称面对一点的z坐标进行反射。
以xy平面为对称面对一点的z坐标进行反射。
手向性
在三维空间中,有3D向量V1,V2,V3构成的坐标系的基&具有手向性。对于右手基,有(V1*V2). V3>0。也就是说,在一个右手坐标系中,v1,v2的叉积的方向与v3的方向形成一个锐角。如果&是一个正交规范的右手基,则有v1*v2=v3。若(v1*v2).v3<0,那么&是左手基。
进行奇数次反射操作就会改变手向性,偶数次反射相当于一次旋转。通过观察3x3矩阵的行列式,就可以判定矩阵是否存在反射。若M的行列式是负的,则存在反射,用M对任意基的向量进行变换操作后,基的手向性都会发生改变。如果行列式是正的,那么M不改变手向性。
正交矩阵M的行列式的值只能是1或-1.若detM=1,矩阵M只存在旋转;如果为-1,那么M表示旋转之后再进行一次反射。
1.2缩放变换
简单来说,对于统一缩放可以理解为向量P乘以一个常数a,即P’ = aP。在三维空间里可以用矩阵的乘积表示。
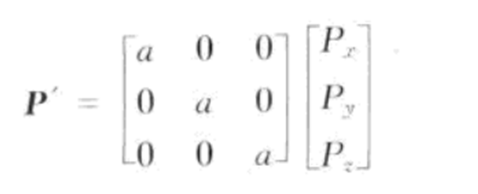
如果是在xyz轴以不同的值进行缩放向量,那么可以这种缩放为非统一缩放。
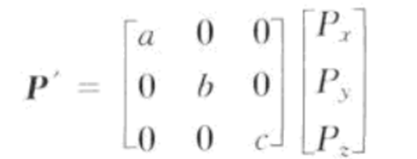
如果在3个任意轴上进行非统一缩放,就要用到复杂的缩放过程。假设以系数a沿U轴方向,以系数b沿V轴方向,以系数c沿W轴方向进行缩放,可以先从坐标系(U,V,W)变换到坐标系(i,j,k),然后在(i,j,k)坐标系进行缩放运算,最后在还原到(U,V,W)坐标系。

1.3旋转变换
首先讲一下在二维平面上的旋转,也就是在平面直角坐标系上进行旋转。假设一个向量P(Px,Py),要想求得相对于它自身旋转a度角后的向量P’。我们就需要根据P逆时针旋转90度得到其正交的向量Q(-Py,Px)。可以将P,Q看做该坐标系的一对正交基,则P’可以被P和Q表示为:
P’ = Pcosa + Qsina; (1)
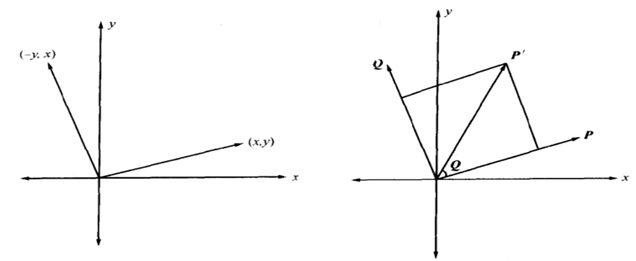
可以确定P’的x,y分量为:
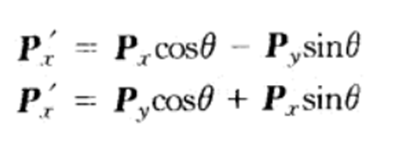
可以改写成矩阵的形式:
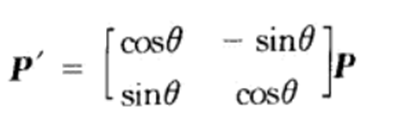
引申一下:将单位矩阵的第三行和第三列加入P’矩阵中可得: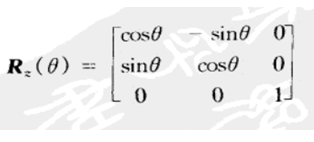
,该矩阵是绕z轴的三维旋转。
同样可以得到绕x轴和y轴旋转角度的3x3旋转矩阵。
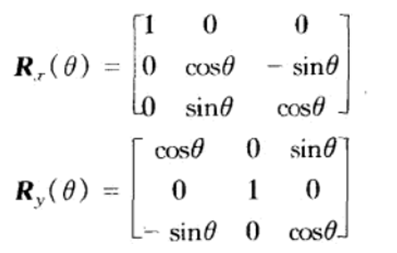
绕任意轴旋转
假设向量P绕一个任意轴旋转Θ角,这里的任意轴以单位向量A表示,可以将向量P分解为垂直于和平行于A的分量P1, P2。由于平行分量P2在平行于A,则在旋转过程中保持不变,主要求的是P1的旋转。
由于A是一个单位向量,对于P在A上的投影,可以表示为:projAP = (A.P)A;
P垂直于A的分量可表示为:perpAP = P – (A.P)A;
现将垂直于A的分量进行旋转,然后加上projAP就可以得到最终的旋转结果。
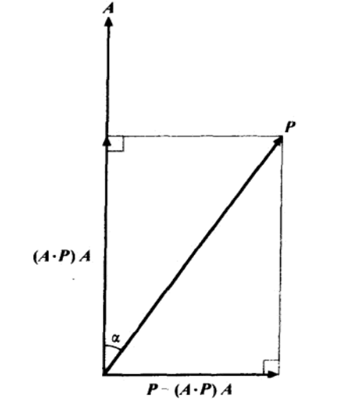
垂直分量的旋转是如何得到的呢?
垂直分量的旋转是在垂直于A轴的平面内进行的。可以用perpAP与perpAP逆时针方向旋转90度所形成的向量的线性组合来表示旋转后的向量。如上图所示,假设a是原向量P和A轴之间的夹角。perpAP的长度等于||P||sina,那么perpAP绕A轴逆时针旋转90度的向量perpAP’就是A与P的叉积。
那么perpAP旋转Θ角可以表示为:[P-(A.P)A]cosΘ + (A x P)sinΘ。 (2)
(2)式的推出可以参考(1)式。
加上projAP = (A.P)A,就可以得到P绕A轴的旋转公式:
P’ = PcosΘ + (A x P)sinΘ + A(A.P)(1-cosΘ); (3)
将(3)式换成矩阵的表达形式:
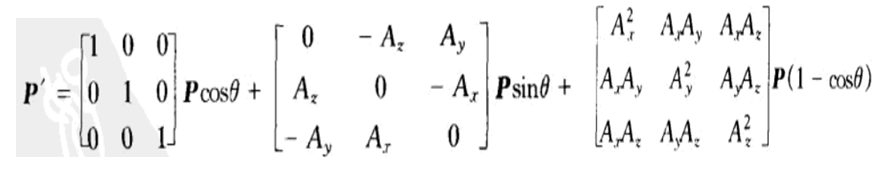
合并公式中的相同项,令C=cosΘ,S=sinΘ,得到表示向量绕A轴旋转Θ角的旋转矩阵RA(Θ).
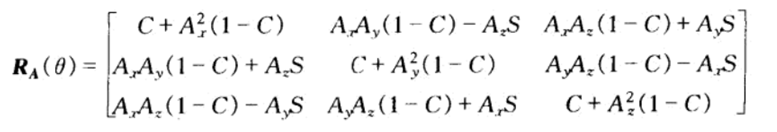
1.4齐次坐标
关于平移操作,不能用3 x 3矩阵表示,把点P从一个坐标系平移到另一个坐标系,只需要简单地添加偏移向量,不会影响到坐标轴的方向和尺度。
P’ = MP + T (4)
其中M为3 x 3可逆矩阵,T是3D平移向量。利用(4)式进行两次操作可得到:
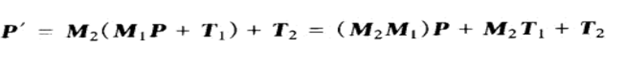 (5)
(5)
若是要进行n次操作时,必须知道每次变换过程中的矩阵分量MnMn-1和平移分量MnTn-1+Tn。
我们利用四维变换可以将M和T统一起来,就可以建立一个四维4 x 4矩阵来表示平移操作。方法是给3D点P增加一个坐标,并将这个扩展的第四个坐标称之为w坐标,其值设为1。
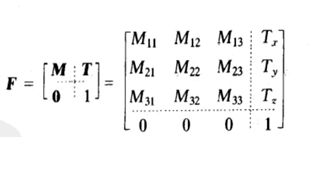 (6)
(6)
将矩阵F乘以向量(Px,Py,Pz,1),就等价于(4)式对向量的x,y,z坐标进行变换,同时保持w为1。
从公式(4)中可以解出 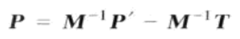 (7)
(7)
因此可以从公式(6)中得到4 x 4矩阵F的逆矩阵F-1为:
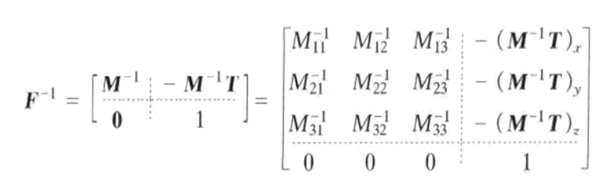 (8)
(8)
可以验证(8)式的正确性:
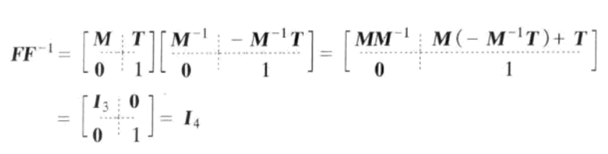
3D游戏与计算机图形学中的数学方法-变换的更多相关文章
- 3D游戏与计算机图形学中的数学方法-四元数
说实话关于四元数这一节真的是不好懂,因为里面涉及到好多数学知识,单说推出来的公式就有很多.不怕大家笑话,对于四元数的学习我足足花了两天的时间,包括整理出这篇文章.在前面一章我写到了“变换”,这也是总结 ...
- 3D游戏与计算机图形学中的数学方法-点线面
<易传·系辞上传>:”易有太极,是生两仪,两仪生四象,四象生八卦.” 借用一下古代先人们的智慧引一下本文的主题-三维图形中的点线面,在三维几何中也有一句话可以和上面的话相对应:由点成线,由 ...
- 3D游戏与计算机图形学中的数学方法-视截体
视截体用来表示一个空间的范围,位于这个空间范围内的三维场景的任何物体都可以被看到. 视截体由六个平面围成,其中的四个平面与场景的边界相对应,分别被称为左,右,底,顶视截面.另外两个平面称为近视截面和远 ...
- Mathematics for Computer Graphics数学在计算机图形学中的应用 [转]
最近严重感觉到数学知识的不足! http://bbs.gameres.com/showthread.asp?threadid=10509 [译]Mathematics for Computer Gra ...
- 3D游戏开发之UE4中的集合:TSet容器
好久没有更新了,最近一直在老家过年,网络不通的,今天才有时间更新一集. 一.TSet<T>是什么 UE4中,除了TArray动态数组外,还提供了各种各样的模板容器.这一节,我们就介绍集合容 ...
- 计算机图形学中使用Turbo C++画图步骤
一.下载安装Turbo C++ 我安装的是Turbo C++ 3.2.2.0下载链接 二.画图 1.打开Turbo C++,点击右下角start turbo C++ 2.点击file ->new ...
- JS中的数学方法
1 . Math.ceil() 向上取整 2. Math.floor() 向下取整 3. Math.round() 四舍五入取整 4. Math.random() 生成 ...
- Java中的数学方法
直接用代码 public class TestNumber { public static void main(String[] args) { float f1 = 5.4f; float f2 = ...
- 计算机图形学学习方法和相关书籍,做游戏,GIS,虚拟现实,三维引擎的都能够看看.
本书參照<<图形学扫盲>> 整理的,原文内容引子: http://www.cppblog.com/lai3d/archive/2008/12/30/70796.html 前言: ...
随机推荐
- unity, 荧光效果(bloom)
----更新:2015-5-31 详细实现过程见:http://www.cnblogs.com/wantnon/p/4542172.html ----原帖:2015-4-16 用摄像机特效只能做全屏b ...
- js实现精确统计网站访问量的代码分享
JS 精确统计网站访问量. 代码如下: /** * vlstat 浏览器统计脚本 */ var statIdName = "vlstatId"; var xmlHttp; /** ...
- [svc]linux日志和安全日志
last详解: http://www.cnblogs.com/kerrycode/p/4223751.html
- 关于haproxy负载均衡的算法整理
目前haproxy支持的负载均衡算法有如下8种: 1:roudrobin 表示简单的轮询,每个服务器根据权重轮流使用,在服务器的处理时间平均分配的情况下这是最流畅和公平的算法.该算法是动态的,对于实例 ...
- Django---时间的时区问题
在用django1.8版本做项目的时候遇到时间的存储与读取不一致的问题,网上找了很多帖子,但都没有讲明白.本文将在项目中遇到的问题及如何解决的尽可能详细的记录下来,当然本文参考了网上大量相关文章. 在 ...
- Spark学习笔记总结-超级经典总结
Spark简介 spark 可以很容易和yarn结合,直接调用HDFS.Hbase上面的数据,和hadoop结合.配置很容易. spark发展迅猛,框架比hadoop更加灵活实用.减少了延时处理,提高 ...
- javascript基础学习--HTML DOM
写在前面的话:由于学校没有开过javascript这门课,所以平时用javascript时都是用到什么就去搜什么样的代码,但是在工作中有时候搜来的代码总是有那么点小问题,而当自己想去修改时,却又无从下 ...
- #include <algorithm>中sort的一般用法
1.sort函数的时间复杂度为n*log2(n),执行效率较高. 2.sort函数的形式为sort(first,end,method)//其中第三个参数可选. 3.若为两个参数,则sort的排序默认是 ...
- 屏幕相关操作(XE10.1+WIN8.164)
相关资料: http://www.bianceng.cn/Programming/Delphi/201104/25455.htm http://blog.csdn.net/anbangs/articl ...
- dubbox2.8.4例子教程一
简介 Dubbo是一个来自阿里巴巴的开源分布式服务框架,当当根据自身的需求,为Dubbo实现了一些新的功能,包括REST风格远程调用.Kryo/FST序列化等等.并将其命名为Dubbox(即Dubbo ...
