[BZOJ1857][SCOI2010]传送带-[三分]

Description

传送门

Solution

三分套三分。代码简单但是证明苦兮兮。。

假如我们在AB上选了一个点G，求到该点到D的最小时间。

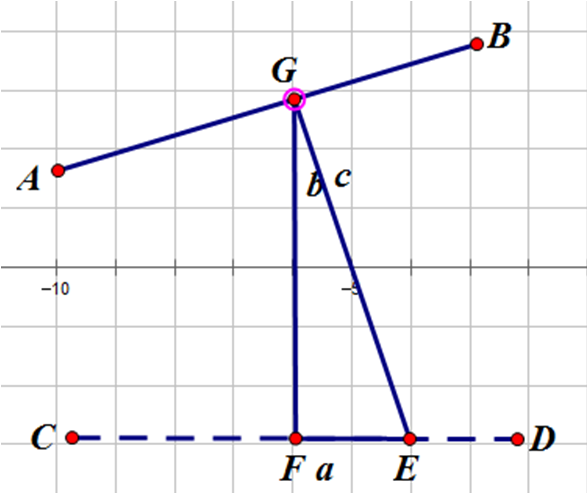
图中b与CD垂直。设目前从G到D所耗时间最短的路径为G->E->D，可知E绝对不会在F右侧。

设函数f(a)=GE+ED-FD=sqrt(a^2+b^2)/r-a/q，我们要证它是单峰的。

设1/r=x,1/q=y。

则GE+ED-FD=x*sqrt(a^2+b^2)-ay。

1，如果x<y，最优方案必定为E与D重合，显然；

2，如果x>y，设y=kx(k<1)。

　则GE+ED-FD=x*sqrt(a^2+b^2)-akx=x*(sqrt(a^2+b^2)-ak)。

　sqrt(a^2+b^2)的上升趋势会越来越快（因为随着a的增加，该式受b^2影响越小），而ak的函数解析式是一条直线，故f(a)是单峰的。

可能讲的有点玄学可以用几何画板画一下哈哈。

接下来我们探讨G的选择。x,y还是按照上面的定义。g(AG)=A->G->E->D的时间，现在我们要证明g是单峰的。假如x<y：

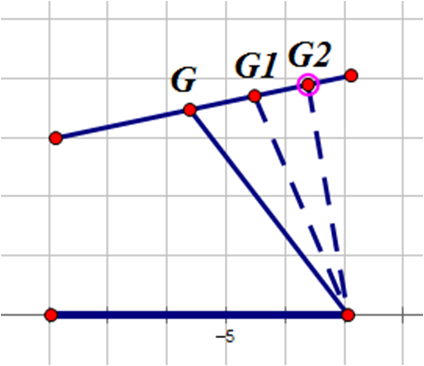
如图，证明显然。

假如x>y:

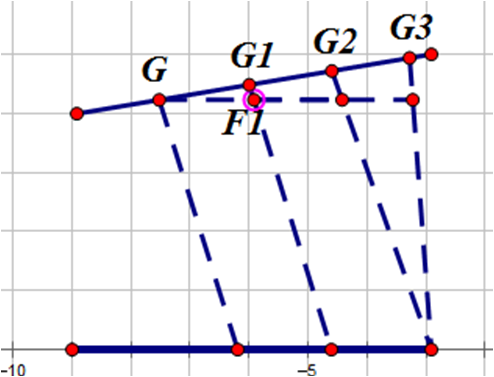
GF1//CD，可知g(AG1)-g(AG)=(GG1)/p+(G1F1)/r-(GF1)/q。又因为三角形三边成比例，则在G2之前的g(AG)必定是向上或者向下的。

设点G'使得G'D垂直于AB，如果G2在G'前面：

考虑G2G'(G'图中未标出)，若先前的g是下降的，则在这一段的g必定也是下降的。反之如图：

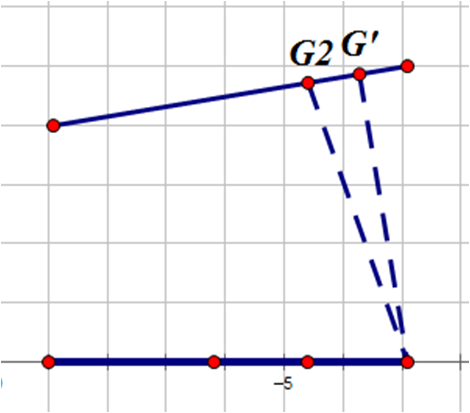
然后。。然后就证不下去了。。。

如果有大佬知道的话还请不吝赐教，我必万分感激！

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int p,q,rr;
struct P{double x,y;
    friend P operator+(P x,P y){return P{x.x+y.x,y.y+x.y};}
    friend P operator/(P x,double y){return P{x.x/y,x.y/y};}
}a,b,c,d,l,r,mid1,mid2;
double dis(P x,P y){return sqrt((x.x-y.x)*(x.x-y.x)+(y.y-x.y)*(y.y-x.y));}
double solve(P x)
{
    P L,R,Mid1,Mid2;
    L=c;R=d;
    while (dis(L,R)>1e-)
    {
        Mid1=(L+L+R)/3.0;Mid2=(L+R+R)/3.0;
        if (dis(x,Mid1)/rr+dis(Mid1,d)/q<dis(x,Mid2)/rr+dis(Mid2,d)/q)
            R=Mid2;else L=Mid1;
    }
    return dis(x,L)/rr+dis(L,d)/q;
}
double ans;
int main()
{
    scanf("%lf%lf%lf%lf%lf%lf%lf%lf%d%d%d",&a.x,&a.y,&b.x,&b.y,&c.x,&c.y,&d.x,&d.y,&p,&q,&rr);
    l=a;r=b;
    while (dis(r,l)>1e-)
    {
        mid1=(l+l+r)/3.0;mid2=(r+r+l)/3.0;
        if (solve(mid1)+dis(a,mid1)/p<solve(mid2)+dis(a,mid2)/p) r=mid2;else l=mid1;
    }
    printf("%.2f",dis(a,l)/p+solve(l));
}