走迷宫（用队列bfs并输出走的路径）

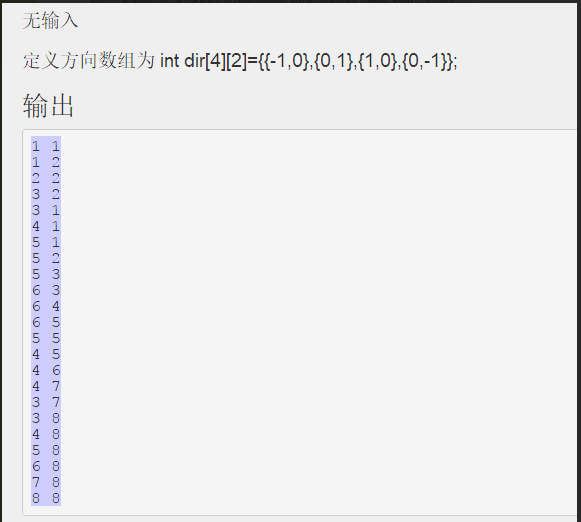
#include <iostream>
#include <stack>
#include <string.h>
#include <stdio.h>
#include<queue>
#include<algorithm>
using namespace std;
int a[][]=
{
    {,,,,,,,,,},{,,,,,,,,,},
    {,,,,,,,,,},{,,,,,,,,,},
    {,,,,,,,,,},{,,,,,,,,,},
    {,,,,,,,,,},{,,,,,,,,,},
    {,,,,,,,,,},{,,,,,,,,,}
};
int dir[][]={{-,},{,},{,},{,-}};
int vis[][];//用来标记有没有走过（有没有在队列中)
int b[][];//用来记录bfs的过程
struct Node
{
    int x,y;
};
queue<Node>q;
int main()
{
    memset(b,,sizeof(b));
    memset(vis,,sizeof(vis));
    while(!q.empty()) q.pop();//初始化队列
 
    Node start;
    start.x=;
    start.y=;
    vis[][]=;
    b[][]=;
    q.push(start);//把起点放进队列
    bool f=;
    while(!q.empty())
    {
        Node temp;
        temp=q.front();//取出队头元素
        q.pop();
        int x=temp.x;
        int y=temp.y;
        if(x==&&y==)//若走到了
        {
            f=;
            Node road[];//用来记录路径
            //for(int i=1;i<=8;i++)//可以通过输出b数组来观察bfs的实现过程
            //{
            //    for(int j=1;j<=8;j++)
            //    {
            //        printf("%5d",b[i][j]);
            //    }
            //    cout<<endl;
            //}
            //cout<<b[8][8]<<endl;
            int k=;
            while(!(x==&&y==))//通过b数组来找到之前是哪一个点走到x，y的
            {
                road[k].x=x;
                road[k++].y=y;
                for(int i=;i<;i++)
                {
                    int xx=x+dir[i][];
                    int yy=y+dir[i][];
                    if(xx<||yy<||xx>||yy>) continue;//超出范围的不要
                    if(b[xx][yy]==b[x][y]-)
                    {
                        x=xx;//倒退回去
                        y=yy;
                        break;//一定要跳出，要把更新的x，y放到road里
                    }
                }
            }
            road[k].x=;//别忘了把起点放进去
            road[k].y=;
            for(int i=k;i>=;i--)//输出路径
            {
                cout<<road[i].x<<" "<<road[i].y<<endl;
            }
        }
        if(f==) //找到路了就不用再跑大循环了
            break;
 
        for(int i=;i<;i++)//遍历四个方向
        {
            int xx=x+dir[i][];
            int yy=y+dir[i][];
            if(a[xx][yy]==&&vis[xx][yy]==)
            {
                vis[xx][yy]=;
                Node New;
                New.x=xx;
                New.y=yy;
                b[xx][yy]=b[x][y]+;//用来标记走到（xx，yy）是第几步
                q.push(New);//放进队列
            }
        }
    }
    return ;
}