[codeforces 516]A. Drazil and Factorial

[codeforces 516]A. Drazil and Factorial

试题描述

Drazil is playing a math game with Varda.

Let's define 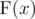 for positive integer x as a product of factorials of its digits. For example, .

First, they choose a decimal number a consisting of n digits that contains at least one digit larger than 1. This number may possibly start with leading zeroes. Then they should find maximum positive number x satisfying following two conditions:

1. x doesn't contain neither digit 0 nor digit 1.

2.  = .

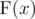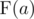Help friends find such number.

输入

The first line contains an integer n (1 ≤ n ≤ 15) — the number of digits in a.

The second line contains n digits of a. There is at least one digit in a that is larger than 1. Number a may possibly contain leading zeroes.

输出

Output a maximum possible integer satisfying the conditions above. There should be no zeroes and ones in this number decimal representation.

输入示例

输出示例

数据规模及约定

见“输入”

题解

这个题相当有意思，我看 n 那么小，那一定是 dp 了，然而写完了才发现 F(a) 会爆 long long，所以只好另辟蹊径。后来发现一个性质：只要把 a 的每一位数都尽量的分出最多数出来，然后再拼到一起就好了，这个不难证明，就是个贪心，若将两个数的阶乘合并成一个数的阶乘，则答案会减少 1，一定不优。

现在的任务是把 2, 3, 4, ... , 9 这些 1 位数尽量多地分解，我发现刚刚的 dp 没有白写：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <queue>
#include <cstring>
#include <string>
#include <map>
#include <set>
using namespace std;

const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
    if(Head == Tail) {
        int l = fread(buffer, 1, BufferSize, stdin);
        Tail = (Head = buffer) + l;
    }
    return *Head++;
}
int read() {
    int x = 0, f = 1; char c = getchar();
    while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
    while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
    return x * f;
}

#define maxn 6000010
#define maxk 20
int n, sum, fact[maxk], F[maxn], f[maxn][11];
char num[maxk];
bool vis[maxn];

bool Less(int* a, int* b) {
	for(int i = 9; i >= 2; i--) if(a[i] != b[i])
		return a[i] < b[i];
	return 0;
}

int main() {
	n = read();
	scanf("%s", num + 1);

	fact[0] = 1;
	for(int i = 1; i <= 9; i++) fact[i] = fact[i-1] * i;
	sum = 1;
	for(int i = 1; i <= n; i++) sum *= fact[num[i]-'0'];
	vis[1] = 1;
	for(int i = 1; i <= sum; i++) if(vis[i]) {
//		printf("%d ", i);
		for(int k = 2; k <= 9 && fact[k] * i <= sum; k++) {
			int t = fact[k] * i;
//			printf("[%d]", t);
			vis[t] = 1;
			if(F[t] < F[i] + 1) {
				F[t] = F[i] + 1;
				memcpy(f[t], f[i], sizeof(f[i]));
				f[t][k]++;
			}
			if(F[t] > F[i] + 1) continue;
			f[i][k]++;
			if(Less(f[t], f[i])) memcpy(f[t], f[i], sizeof(f[i]));
			f[i][k]--;
		}
	}

	for(int i = 9; i >= 2; i--)
		for(int j = 1; j <= f[sum][i]; j++)
			putchar(i + '0');
	putchar('\n');

	return 0;
}

就依次输入，结果记一下，在主程序中打个表：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <queue>
#include <cstring>
#include <string>
#include <map>
#include <set>
using namespace std;

const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
    if(Head == Tail) {
        int l = fread(buffer, 1, BufferSize, stdin);
        Tail = (Head = buffer) + l;
    }
    return *Head++;
}
int read() {
    int x = 0, f = 1; char c = getchar();
    while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
    while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
    return x * f;
}

#define maxn 20
int n, cnt[maxn];
char num[maxn];

int main() {
	n = read();
	scanf("%s", num + 1);

	for(int i = 1; i <= n; i++) {
		if(num[i] == '9') {
			cnt[7]++; cnt[3]++; cnt[3]++; cnt[2]++;
		}
		if(num[i] == '8') {
			cnt[7]++; cnt[2]++; cnt[2]++; cnt[2]++;
		}
		if(num[i] == '7') {
			cnt[7]++;
		}
		if(num[i] == '6') {
			cnt[5]++; cnt[3]++;
		}
		if(num[i] == '5') {
			cnt[5]++;
		}
		if(num[i] == '4') {
			cnt[3]++; cnt[2]++; cnt[2]++;
		}
		if(num[i] == '3') {
			cnt[3]++;
		}
		if(num[i] == '2') {
			cnt[2]++;
		}
	}

	for(int i = 7; i >= 2; i--)
		for(int j = 1; j <= cnt[i]; j++) putchar(i + '0');
	putchar('\n');

	return 0;
}

A 啦！