NOIP 2007 普及组

NOIP 2007 普及组（DONE）

注：本文不附原题，可上Luogu有题对照查询。

1.CPU：即中央处理器，由运算器+控制器+寄存器组成，不含主板（但CPU是装在主板上的）。

2.二维表即常见的二维数组，例如一个学生信息的二维表如下：

姓名	学号	成绩
ztr	114	-1
fyc	514	100

这不就是二维数组？

3.UB（undefined behaviour）往往指的是C++程序中的未定义行为，而非容量单位。
常见容量单位及其转换： <script type="math/tex;mode=inline">1TB=2^{10}GB=2^{20}MB=2^{30}KB=2^{40}B=2^{43}b</script>1TB=2^{10}GB=2^{20}MB=2^{30}KB=2^{40}B=2^{43}b

4.ASCII 码（American Standard Code for Information Interchange）是美国国家交换标准代码，现已成为世界交换代码标准。

5.一个完整的计算机系统包括硬件系统和软件系统两大部分，硬件系统包括运算器、控制器、存储器、输入设备、输出设备五大部分；软件系统则包括系统软件（即操作系统）以及应用软件。

6.IT（Information Technology）即信息技术。

7.L(Local)，所以是局域网，对应的还有WAN（广域网）和MAN（城域网）。

8.为了更快的进行检索工作（如Windows中的查找文件），可以保留适度的冗余数据，平衡维护的开销。

9.（参考意义不大）只有gcc，g++和Free Pascal。

10.RAM（Random Access Memory），即随机存取存储器（所谓的内存）可随时读写，断电数据全部丢失。

11.依次排除错误：
A.运行效率绝大多数情况下是更低。
B.在一些底层实现仍需要汇编语言。
D.C没有面向对象，而是面向过程的。

12.易错点是D，这种方法只能是嵌套，记住递归是在函数内部调用自己。A属于历史题，但是可以排除BCD。

13.联想你写程序TLE的时候编译器会提醒吗？

14. <script type="math/tex;mode=inline">(23){10}|(2){10}\;\text{xor}\;(5){10}=(10111)_2|(10)_2\;\text{xor}\;(101)_2=(10111)_2=(23){10}</script>(23){10}|(2){10}\;\text{xor}\;(5){10}=(10111)_2|(10)_2\;\text{xor}\;(101)_2=(10111)_2=(23){10}
其中 | 为逻辑或运算，即在二进制下两者有一个为 1 就是 1。
^（xor）为逻辑异或运算，即在二进制下两者不同才为 1，否则为 0。

15.判断题中条件等价于对三者都不为 0 的情况取反即可。

16.注意并不是汉诺塔问题，而且一定要经过B柱。
其实就是一个栈的操作，参见图片解释（红进蓝出）：

<img src="https://pic2.zhimg.com/v2-5f54cf562998687dd21048092e4fc735_b.jpg" data-caption="" data-size="normal" data-rawwidth="514" data-rawheight="50" class="origin_image zh-lightbox-thumb" width="514" data-original="https://pic2.zhimg.com/v2-5f54cf562998687dd21048092e4fc735_r.jpg"/>

17.反复除八取余（参考十进制转二进制）。

18.数学上的与或非，⋀ 代表与，⋁ 代表或，﹁ 代表非。
D.(1 ⋀ ( 0 ⋁ 0 ) ) ⋀ 1 = ( 1 ⋀ 0 ) ⋀ 1 = 0

19.先转化成十进制在计算。

20.不断找根节点和其在中序遍历中的位置。详情见图。

<img src="https://pic4.zhimg.com/v2-0197d08347f6796aa37d6bb5e905b88f_b.jpg" data-caption="" data-size="normal" data-rawwidth="551" data-rawheight="540" class="origin_image zh-lightbox-thumb" width="551" data-original="https://pic4.zhimg.com/v2-0197d08347f6796aa37d6bb5e905b88f_r.jpg"/>

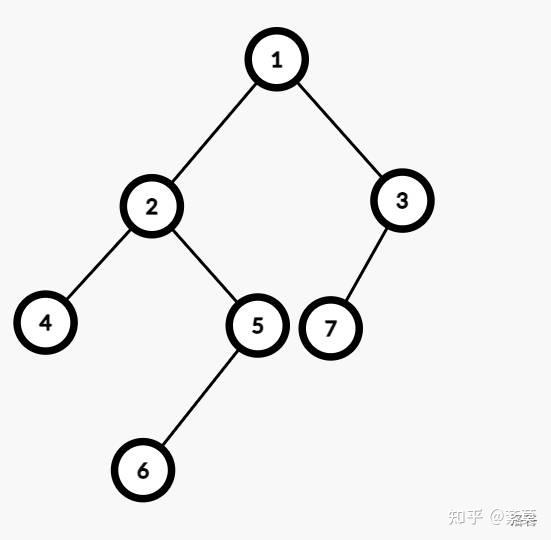
然后按照左右根的顺序遍历二叉树即为答案：4652731。

21.根据提示的思路，明显是按照递归调用来的。
容易发现 <script type="math/tex;mode=inline">S(n,r)=S(n-1,r-1)+r \times S(n-1,r)</script>S(n,r)=S(n-1,r-1)+r \times S(n-1,r) 。
后者就是任选一个加入当前的 r 个集合中，前者是另外开出一个集合来。

22.因为是最短路径，直接标数或者用组合数均可。

<img src="https://pic1.zhimg.com/v2-87cfc9586d00ed4c3eae17b7e402c010_b.jpg" data-caption="" data-size="normal" data-rawwidth="749" data-rawheight="460" class="origin_image zh-lightbox-thumb" width="749" data-original="https://pic1.zhimg.com/v2-87cfc9586d00ed4c3eae17b7e402c010_r.jpg"/>

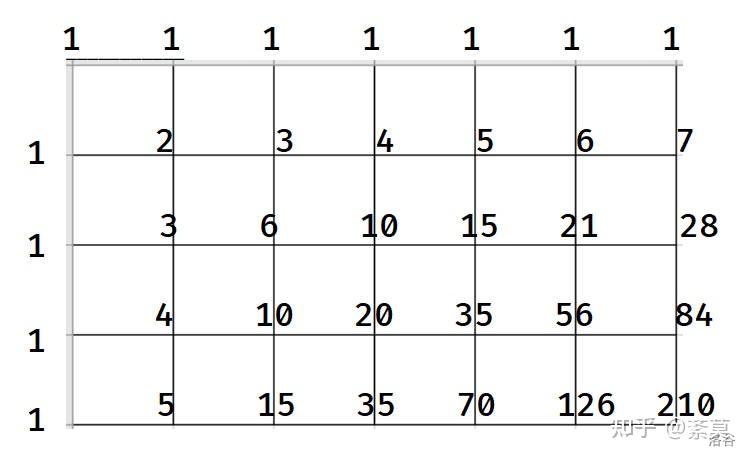
23.没什么意义的计算题。

24.注意 a,b 并没有实质的交换，因此答案不变。
如果代码改成这样才是真正交换了（或者使用一元运算符*）。

#include<stdio.h>
void fun( int &a, int &b ){
    int k;
    k = a; a = b; b = k;
}
int main(){
    int a = 3, b = 6, *x = &a, *y = &b;
    fun(a,b);
    printf( "%d,%d ", a, b );
}

25.该代码的含义为素数筛（50以内），即埃氏筛，注意下答案十个一行输出。

26.发现带 “-” 的地方就是补全相关的字母或者数字，这题在TG复赛就是[NOIP2007 提高组] 字符串的展开

27.前两处容易发现是 i 和 j 向中间靠拢，然后不断交换，因此是一加一减，第三处是判断退出条件，发现输入为 -1 时要退出。最后进行操作，参见函数参数的定义。

28.即P1228 地毯填补问题。
例如下图：

<img src="https://pic3.zhimg.com/v2-9a6b0fd7714c5a530cc64f004c5a484a_b.jpg" data-caption="" data-size="small" data-rawwidth="161" data-rawheight="161" class="content_image" width="161"/>

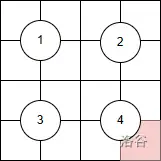
红色表示标记方格，四个格子标记为一个大区，共有4个大区。
第一空，siz=1，证明不能再分，递归边界应该返回。
第二空，参考下面的条件，可以知道答案是dr<tr+s&&dc<tc+s
后面四个以第三空为例，根据第二空的答案得到这一判断的意义是标记的格子是否在第一区内，如果不是，那么第一区的右下角就应该被看作一个新的标记（参考给出的语句），那么，所以左上角坐标不变，标记格子照抄，方格大小改成s，即chessboard(tr,tc,tr+s-1,tc+s-1,s)。