动态数组（Array）

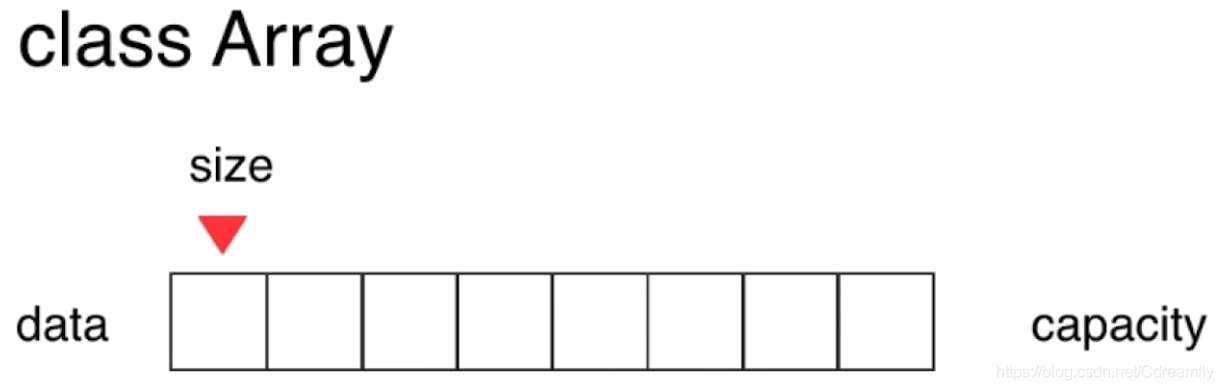
Array

• 存储具有一对一逻辑关系数据的存储顺序结构。
• 数组最大的优点：快速查询，最好应用于索引有语义的情况。
  
  

插入元素

template<typename T>
bool Array<T>::add(const int index, const T& e)
{
	if (index<0 || index>size)return false;		//判断索引是否正确
	if (size == capacity)resize(1.5 * capacity);	//判断空间是否足够，不够扩容为当前的2倍
	for (int i = size - 1; i >= index; --i)		//从后向前循环
	{
		data[i + 1] = data[i];					//全部元素向后移一位
	}
	data[index] = e;							//插入元素
	++size;										//数组元素的个数+1
	return true;
}

扩容与缩减

template<typename T>
void Array<T>::resize(const int newcapacity)
{
	T* newdata = new T[newcapacity];	//创建新的传入大小数组空间
	for (int i = 0; i < size; ++i)	//把原本的数组元素放入新的数组空间
	{
		newdata[i] = data[i];
	}
	delete[] data;	//释放原数组的空间
	data = newdata;		//把原本的数组指向新的数组
	newData = nullptr;
	capacity = newcapacity;	//新的空间大小给原本的空间大小
}

删除元素

template<typename T>
T Array<T>::remove(const int index)
{
	if (index<0 || index>size)return -1;	//判断索引是否正确
	T ret = data[index];					//保存临时元素
	for (int i = index + 1; i < size; ++i)
	{
		data[i - 1] = data[i];				//从要插入的元素后一位所有元素向前移一位
	}
	--size;	//元素个数-1
	if (size == capacity / 4 && capacity / 2 != 0)	//判断元素个数是否为数组容量的1/4并且数组空间不为0
	{
		resize(capacity / 2);	//调用resize传入当前容量的一半
	}
	return ret;		//返回被删除的元素
}

时间复杂度

均摊复杂度

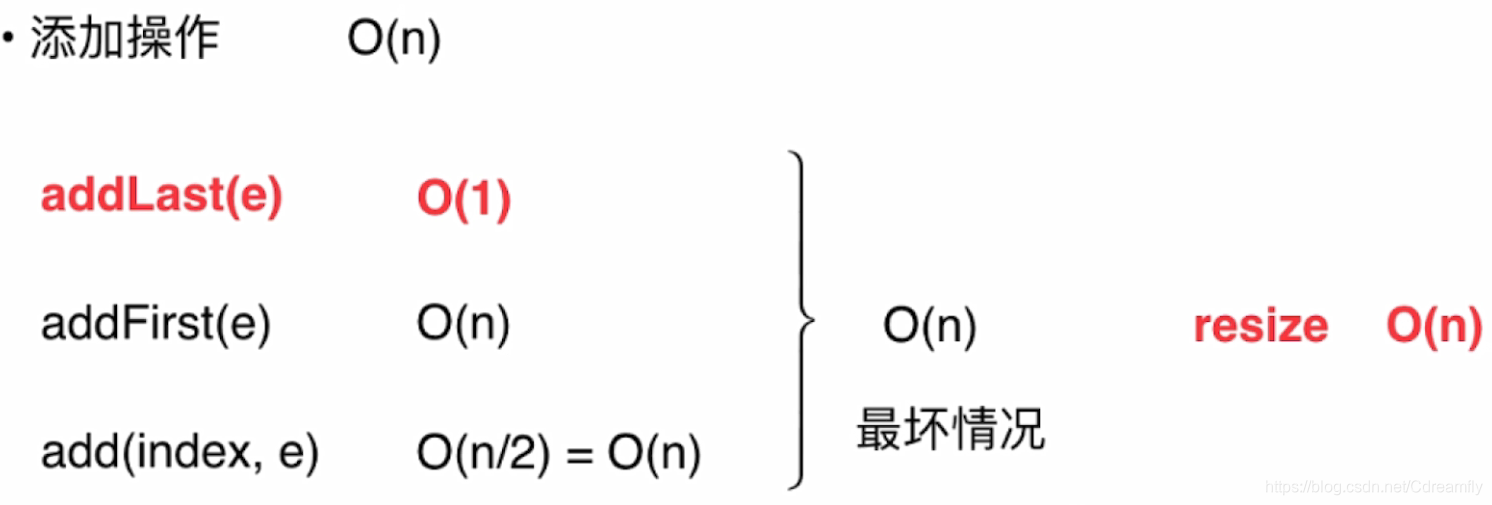
  9次addLast操作，触发resize，总共进行了17次基本操作，平均每次addLast操作，进行2次基本操作。

  假设capacity = n，n+1次addLast，触发resize，总共进行2n+1次基本操作，平均每次addLast操作进行2次基本操作。

  这样均摊计算时间复杂度是O(1)，同理removeLast操作，均摊复杂度也为O(1)。

代码清单

Array.h

#pragma once
#include<iostream>
template<typename T>
class Array
{
public:
	//无参构造
	Array() :size(0), capacity(10)
	{
		data = new T[10];	//默认初始化10个空间
	}
	//有参构造
	Array(int capacity) :size(0), capacity(capacity)
	{
		data = new T[capacity];
	}
	//返回元素个数
	int getSize()const;
	//返回数组容量
	int getCapacity()const;
	//返回第一个元素
	T getFirst();
	//返回最后一个元素
	T getLast();
	//判断是否为空
	bool isEmpty()const;
	//插入元素
	bool add(const int index, const T& e);
	//头插
	bool addFirst(const T& e);
	//尾插
	bool addLast(const T& e);
	//查找数组中是否存在该元素
	bool contains(const T& e)const;
	//查找数组中元素的索引，不存在返回-1
	int find(const T& e)const;
	//删除索引元素，返回删除元素
	T remove(const int index);
	//删除头，返回头
	T removeFirst();
	//删除尾，返回尾
	T removeLast();
	//设置索引值
	bool set(const int index, const T& e);
	//获取索引值
	T get(const int index)const;
	//打印元素
	void print()const;
	//释放空间
	~Array();

public:
void swap(const int i, const int j) {
    if (i < 0 || i >= size || j < 0 || j >= size) {
        throw Range();
    }
    T t = data[i];
    data[i] = data[j];
    data[j] = t;
}

Array(T arr[], const int n) : size(n), capacity(n) {
   data = new T[n];
    for (int i = 0; i < n; ++i) {
        data[i] = arr[i];
    }
}

private:
	void resize(const int newcapacity);	//重新分配空间
	T* data;
	int size;	//数组大小
	int capacity;	//数组容量
};

template<typename T>
int Array<T>::getSize() const
{
	return size;	//返回数组长度
}

template<typename T>
int Array<T>::getCapacity() const
{
	return capacity;	//返回数组容量
}

template<typename T>
inline T Array<T>::getFirst()
{
	return get(0);
}

template<typename T>
inline T Array<T>::getLast()
{
	return get(size - 1);
}

template<typename T>
bool Array<T>::isEmpty() const
{
	return size == 0;	//判断是否为空，
}

template<typename T>
bool Array<T>::add(const int index, const T& e)
{
	if (index<0 || index>size)return false;		//判断索引是否正确
	if (size == capacity)resize(2 * capacity);	//判断空间是否足够，不够扩容为当前的2倍
	for (int i = size - 1; i >= index; --i)		//从后向前循环
	{
		data[i + 1] = data[i];					//全部元素向后移一位
	}
	data[index] = e;							//插入元素
	++size;										//数组元素的个数+1
	return true;
}

template<typename T>
bool Array<T>::addFirst(const T& e)
{
	return add(0, e);	//调用add从0号索引元素插入
}

template<typename T>
bool Array<T>::addLast(const T& e)
{
	return add(size, e);	//调用add从size号索引元素插入
}

template<typename T>
bool Array<T>::contains(const T& e) const
{
	for (int i = 0; i < size; ++i)	//遍历是否有查找的元素
	{
		if (data[i] == e)return true;
	}
	return false;
}

template<typename T>
int Array<T>::find(const T& e) const
{
	for (int i = 0; i < size; ++i)	//遍历是否有查找的元素，有返回索引，无返回-1
	{
		if (data[i] == e)return i;
	}
	return -1;
}

template<typename T>
T Array<T>::remove(const int index)
{
	if (index<0 || index>size)return -1;	//判断索引是否正确
	T ret = data[index];					//保存临时元素
	for (int i = index + 1; i < size; ++i)
	{
		data[i - 1] = data[i];				//从要插入的元素后一位所有元素向前移一位
	}
	--size;	//元素个数-1
	if (size == capacity / 4 && capacity / 2 != 0)	//判断元素个数是否为数组容量的1/4并且数组空间不为0
	{
		resize(capacity / 2);	//调用resize传入当前容量的一半
	}
	return ret;		//返回被删除的元素
}

template<typename T>
T Array<T>::removeFirst()
{
	return remove(0);		//删除0号索引元素
}

template<typename T>
T Array<T>::removeLast()
{
	return remove(size - 1);	//删除size-1号索引元素
}

template<typename T>
bool Array<T>::set(const int index, const T& e)
{
	if (index<0 || index>size)return false;	//判断索引元素是否正确
	data[index] = e;						//设置索引的新元素
	return true;
}

template<typename T>
T Array<T>::get(const int index) const
{
	if (index<0 || index>size)return -1;	//判断索引元素是否正确
	return data[index];						//返回索引元素
}

template<typename T>
void Array<T>::print() const
{
	std::cout << "Array:size = " << size << "	Array:capacity = " << capacity << std::endl;
	std::cout << "Array:data = " << "[";
	for (int i = 0; i < size; ++i)
	{
		std::cout << data[i] << ",";
	}
	std::cout << "]" << std::endl;
}

template<typename T>
Array<T>::~Array()
{
	delete[] data;	//释放空间
	data = nullptr;
}

template<typename T>
void Array<T>::resize(const int newcapacity)
{
	T* newdata = new T[newcapacity];	//创建新的传入大小数组空间
	for (int i = 0; i < size; ++i)	//把原本的数组元素放入新的数组空间
	{
		newdata[i] = data[i];
	}
	delete[] data;	//释放原数组的空间
	data = newdata;		//把原本的数组指向新的数组
	newData = nullptr;
	capacity = newcapacity;	//新的空间大小给原本的空间大小
}

main.cpp

#include"Array.h"
using namespace std;

int main()
{
	Array<int>* arr = new Array<int>(10);
	for (int i = 0; i < 10; ++i)
	{
		arr->addLast(i);
	}
	arr->print();
	cout << endl;
	cout << "arr->add(1, 1)" << arr->add(1, 1) << endl;
	arr->print();
	cout << endl;
	cout << "arr->addLast(0) " << arr->addLast(0) << endl;
	arr->print();
	cout << endl;
	cout << "arr->addFirst(0)" << arr->addFirst(0) << endl;
	arr->print();
	cout << endl;
	cout << "arr->contains(0)" << arr->contains(0) << endl;
	arr->print();
	cout << endl;
	cout << "arr->find(0)" << arr->find(0) << endl;
	arr->print();
	cout << endl;
	cout << "arr->get(1)" << arr->get(1) << endl;
	arr->print();
	cout << endl;
	cout << "arr->set(0, 5)" << arr->set(0, 5) << endl;
	arr->print();
	cout << endl;
	cout << "arr->getCapacity()" << arr->getCapacity() << endl;
	arr->print();
	cout << endl;
	cout << "arr->getSize()" << arr->getSize() << endl;
	arr->print();
	cout << endl;
	cout << "arr->isEmpty()" << arr->isEmpty() << endl;
	arr->print();
	cout << endl;
	cout << "arr->remove(1)" << arr->remove(1) << endl;
	arr->print();
	cout << endl;
	cout << "arr->removeFirst()" << arr->removeFirst() << endl;
	arr->print();
	cout << endl;
	cout << "arr->removeLast()" << arr->removeLast() << endl;
	arr->print();
	cout << endl;
	cout << "arr->getFirst" << arr->getFirst() << endl;
	arr->print();
	cout << endl;
	cout << "arr->getLast" << arr->getLast() << endl;
	arr->print();

	delete arr;
	return 0;
}