8.21考试总结(NOIP模拟45)[打表·蛇·购物·ants]

有型的东西终究会消逝，不过……终于，这份回忆还是永远不朽的…

前言

这次考试暴露出来了不少问题。

比如答题策略策略不当导致 T2 的 65pts 暴力根本没有打。

知识遗忘太快不牢固，T4 是之前的一道回滚莫队板子题，我却早已忘光。

实在需调整。

T1 打表

解题思路

一个规律题，但是题面不太友善，大概解释一下。

对于从未操作过的二进制数字，促打表 CPU 与反打表 CPU 都有 \(50\%\) 的概率可以选择一位变成 0 或者 1 。

然后 \(A_i\) 表示 \(k\) 个二进制为最终表示数为 \(i\) 的收益。

题解给了一个结论：

设 \(P(i)\) 表示还剩下有 \(i\) 位没有选择的期望值，这个期望值其实就是剩下的数与正确输出差的平均值。

也就是：\(Ans=\dfrac{\sum\limits_{i=0}^{2^k-1}|A_{ans}-A_i|}{2^k}\)

证明一下，当 \(i=1\) 是只剩下一位没有操作那么两者都会选择同一个，因此柿子成立。

那么 所有 \(P(i)\) 均可以由 \(P(i-1)\) 转移过来，但是 CPU 一定不会选择两次去操作同一位，这样的收益显然是很小的，证毕。

code

#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
const int N=(1<<18)+10,mod=1e9+7;
int k,ans,pos,s[N];
void add(int &x,int y){x+=y;if(x>=mod)x-=mod;}
int ksm(int x,int y)
{
	int temp=1;
	while(y)
	{
		if(y&1)	temp=temp*x%mod;
		x=x*x%mod;
		y>>=1;
	}
	return temp;
}
signed main()
{
	k=read();	pos=read()+1;
	for(int i=1;i<=(1<<k);i++)
		s[i]=read();
	for(int i=1;i<=(1<<k);i++)
		add(ans,abs(s[i]-s[pos]));
	printf("%lld",ksm((1<<k),mod-2)*ans%mod);
	return 0;
}

T2 蛇

解题思路

其实仔细观察我们可以发现路径一定是一个类似于下图的一个左括号之后中间随便反复曲折，然后右边在来一个右括号。

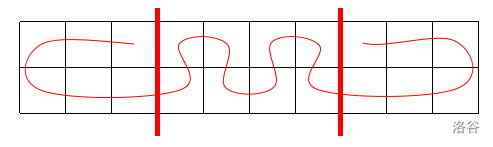
然后对于两个括号形状的东西其实是可以利用 Hash 来判等特殊处理的。

对于中间的部分直接 DP ：

\(f_{i,j,k,0/1}\) 表示第 \(i\) 行，第 \(j\) 列，当前扫到了询问路径的第 \(k\) 个位置，并且是否可以向上或者下转移。

然后优先处理一下左括号形，这里可以维护两个 Hash 分别存储正反的 Hash 值进行判等。

接下来就 DP 处理中间曲折的部分（ \(ch\) 为字符矩阵， \(s\) 为目标字符串），对于 \(ch_{i,j}=s_k\) 的情况进行转移，转移方程如下：

\[f_{i,j,k,0}=f_{i,j,k,0}+f_{i,j-1,k-1,0}+f_{i,j-1,k-1,1}
\]

\[f_{i,j,k,1}=f_{i,j,k,1}+f_{i\;xor\;1,j,k-1,0}
\]

注意转移的时候为了防止当前状态对于之后状态造成过多影响，应该把 k 的循环放在最外层。

对于一个路径而言因为是有向的，因此我们把字符串翻转之后再做一边 DP 就好了。

code

#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
const int N=2e3+10,mod=1e9+7;
const ull base=1331ull;
ull has[N],pre[2][N],suf[2][N],p[N<<1];
int n,m,ans,f[2][N][N<<1][2];
char ch[2][N],s[N<<1];
void Hash()
{
	for(int i=0;i<=1;i++)
		for(int j=1;j<=n;j++)
			pre[i][j]=pre[i][j-1]*base+ch[i][j];
	for(int i=0;i<=1;i++)
		for(int j=n;j>=1;j--)
			suf[i][j]=suf[i][j+1]*base+ch[i][j];
}
ull get_suf(int x,int l,int r){return suf[x][l]-suf[x][r+1]*p[r-l+1];}
ull get_pre(int x,int l,int r){return pre[x][r]-pre[x][l-1]*p[r-l+1];}
ull get_hash(int l,int r){return has[r]-has[l-1]*p[r-l+1];}
void add(int &x,int y){x+=y;if(x>=mod)x-=mod;}
void solve()
{
	Hash();
	for(int i=0;i<=1;i++)
		for(int j=1;j<=n;j++)
		{
			f[i][j][1][0]=(ch[i][j]==s[1]);
			for(int k=2;k<=min(j,m/2);k++)
				if((get_hash(1,k)==get_suf(i^1,j-k+1,j))&&(get_hash(k+1,k<<1)==get_pre(i,j-k+1,j)))
					f[i][j][k<<1][1]=1;
		}
	for(int k=1;k<=m;k++)
		for(int i=0;i<=1;i++)
			for(int j=1;j<=n;j++)
				if(ch[i][j]==s[k])
				{
					add(f[i][j][k][0],f[i][j-1][k-1][0]+f[i][j-1][k-1][1]);
		        	add(f[i][j][k][1],f[i^1][j][k-1][0]);
				}
	for(int i=0;i<=1;i++)
		for(int j=1;j<=n;j++)
			for(int k=0;k<=m;k++)
				if(m-k!=2&&((k&1)==(m&1)))
					add(ans,(f[i][j][k][1]+f[i][j][k][0])*(m==k||(j+(m-k)/2<=n&&get_pre(i,j+1,j+(m-k)/2)==get_hash(k+1,k+(m-k)/2)&&get_suf(i^1,j+1,j+(m-k)/2)==get_hash(k+(m-k)/2+1,m))));
}
void Special_Judge1()
{
	for(int i=0;i<=1;i++)
		for(int j=1;j<=n;j++)
			ans-=(ch[i][j]==s[1]);
}
void Special_Judge2()
{
	for(int i=0;i<=1;i++)
		for(int j=1;j<=n;j++)
			ans-=(ch[i][j]==s[1]&&ch[i^1][j]==s[2]);
}
signed main()
{
	scanf("%s%s%s",ch[0]+1,ch[1]+1,s+1);
	n=strlen(ch[0]+1);	m=strlen(s+1);
	p[0]=1;	for(int i=1;i<=m;i++)	p[i]=p[i-1]*base;
	for(int i=1;i<=m;i++)	has[i]=has[i-1]*base+s[i];
	if(m==1)	Special_Judge1();
	if(m==2)	Special_Judge2();
	solve();
	memset(f,0,sizeof(f));
	for(int i=0;i<=1;i++)	reverse(ch[i]+1,ch[i]+n+1);
	solve();
	printf("%lld",(ans+mod)%mod);
	return 0;
}

T3 购物

解题思路

依然是有一种规律题的感觉。

发现对于数据范围而言，应该是记录两个范围之间的空缺计算更为简便。

先将给出的序列 \(s\) 按从小到大排好序，求出前缀和 \(pre_i=\sum\limits_{j=1}^{i}s_j\)

当前的 \(\dfrac{s_i}{2}\) 大于 \(pre_{i-1}\) 的时候中间就会产生空缺。

因为 \(pre_{i-1}\) 可以造成贡献的上界就是 \(pre_{i-1}\) ，然而除此之外比它大最少的数字（也就是 \(s_i\) ） 的下界就是 \(\lfloor\dfrac{s_i}{2}\rfloor\)

实现的话。。。。

code

#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
const int N=1e5+10;
int n,ans,s[N],pre[N];
signed main()
{
	n=read();
	for(int i=1;i<=n;i++)
		s[i]=read();
	sort(s+1,s+n+1);
	for(int i=1;i<=n;i++)
		pre[i]=pre[i-1]+s[i];
	for(int i=1;i<=n;i++)
	{
		if((s[i]-1)/2<pre[i-1]) continue;
		ans+=(s[i]-1)/2-pre[i-1];
	}
	printf("%lld",pre[n]-ans);
	return 0;
}

T4 ants

解题思路

发现这个题是莫队，但是插入还好，删除操作就异常的恶心。

考虑回滚莫队。

对于每一个块内的询问的左端点而言，我们通过排序之后一定保证右端点是递增的。

因此考虑对于右半部分进行重复利用。

于是，我们对于每一个左端点所在的新的块将用来移动的右指针移动到当前询问的左端点所在的块的末尾，或者说下一个块的开始。

那么当前块右边界以右的部分就可以充分利用了。

对于左半部分直接进行操作并且将操作存入数组，计算完答案之后再逆序挨个撤销。

针对这个题而言的话，就是可以维护两个数组 \(li,ri\) 分别表示在 权值序列 下，当前位置向左或者向右可以连续的数字数量。

举个例子：如果当前的询问区间里的数字是 \(3\;7\;2\;1\) 那么对应到权值序列上就有\(li_2=1,ri_2=1\)

转移的时候就好像向两个序列中插入一个数一样，只需要更改当前插入数字以及序列左右端点的值酒好了。

code

#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
const int N=1e5+10;
int n,m,r,len,maxn,top,pos[N],s[N],ans[N],li[N],ri[N];
struct Node
{
	int l,r,id;
	bool friend operator < (Node x,Node y)
	{
		if(pos[x.l]==pos[y.l])	return x.r<y.r;
		return x.l<y.l;
	}
}q[N];
struct node
{
	bool opt;	int id,val;
}sta[N<<1];
signed main()
{
	n=read();	m=read();
	len=sqrt(n);
	for(int i=1;i<=n;i++)
		s[i]=read(),pos[i]=i/len+1;
	for(int i=1;i<=m;i++)
		q[i].l=read(),q[i].r=read(),q[i].id=i;
	sort(q+1,q+m+1);
	for(int i=1;i<=m;i++)
	{
		if(pos[q[i].l]!=pos[q[i-1].l])
		{
			maxn=0;	r=pos[q[i].l]*len;
			for(int j=1;j<=n;j++)
				li[j]=ri[j]=0;
		}
		while(r<q[i].r)
		{
			r++;
			li[s[r]]=li[s[r]-1]+1;
			ri[s[r]]=ri[s[r]+1]+1;
			int temp=li[s[r]]+ri[s[r]]-1;
			maxn=max(maxn,temp);
			li[s[r]+ri[s[r]]-1]=temp;
			ri[s[r]-li[s[r]]+1]=temp;
		}
		int rec=maxn;
		for(int j=q[i].l;j<=min(q[i].r,pos[q[i].l]*len);j++)
		{
			li[s[j]]=li[s[j]-1]+1;
			ri[s[j]]=ri[s[j]+1]+1;
			sta[++top]=(node){0,s[j]-li[s[j]]+1,ri[s[j]-li[s[j]]+1]};
			sta[++top]=(node){1,ri[s[j]]+s[j]-1,li[ri[s[j]]+s[j]-1]};
			int temp=li[s[j]]+ri[s[j]]-1;
			rec=max(rec,temp);
			li[s[j]+ri[s[j]]-1]=temp;
			ri[s[j]-li[s[j]]+1]=temp;
		}
		while(top)
		{
			if(!sta[top].opt)	ri[sta[top].id]=sta[top].val;
			else	li[sta[top].id]=sta[top].val;
			top--;
		}
		for(int j=q[i].l;j<=min(q[i].r,pos[q[i].l]*len);j++)
			li[s[j]]=ri[s[j]]=0;
		ans[q[i].id]=rec;
	}
	for(int i=1;i<=m;i++)
		printf("%lld\n",ans[i]);
	return 0;
}